SMOTE: метод увеличения числа примеров миноритарного класса

Метод увеличения числа примеров миноритарного класса (Synthetic Minority Over-sampling Technique, SMOTE)  —  это алгоритм предварительной обработки данных, используемый для устранения дисбаланса классов в наборе данных.

В реальном мире нередко приходится обучать модель на наборе данных с очень малым количеством примеров определенного класса. Чаще всего эта проблема возникает при создании классификатора для диагностирования редких заболеваний, выявления производственных дефектов, раскрытия мошеннических транзакций.

Во всех перечисленных сферах применения МО характер данных (очень редкие случаи) не позволяет собрать больше примеров. Однако модель, обученная таким образом, может оказаться малоэффективной.

Одним из способов решения этой проблемы является сокращение числа примеров мажоритарного класса. Иными словами, из набора данных исключаются строки мажоритарного класса, чтобы выровнять количество строк мажоритарного и миноритарного классов.

Тем не менее при таком подходе теряется много данных, которые могли бы быть использованы для обучения модели и повышения ее точности (например, предупреждения чрезмерной предвзятости).

Другим вариантом является увеличение примеров миноритарного класса. Иными словами, случайным образом дублируются образцы миноритарного класса. Проблема этого подхода заключается в том, что он приводит к чрезмерному обучению, поскольку модель обучается на одних и тех же примерах.

Вот здесь на помощь и приходит SMOTE. В общих чертах этот алгоритм можно описать следующим образом.

• Он находит разность между данным образцом и его ближайшим соседом.
• Эта разность умножается на случайное число в интервале от 0 до 1.
• Полученное значение добавляется к данному образцу для формирования нового синтезированного образца в пространстве признаков.
• Подобные действия продолжаются со следующим ближайшим соседом, до заданного пользователем количества образцов.

Рассмотрим алгоритм более подробно. Предположим, у нас есть несбалансированный набор данных (строк одного класса гораздо больше, чем другого). Построим граф подмножества строк миноритарного класса. Будем учитывать только 2 из множества признаков, предполагая, что последующие шаги будут выполняться для всех N измерений в наборе данных.

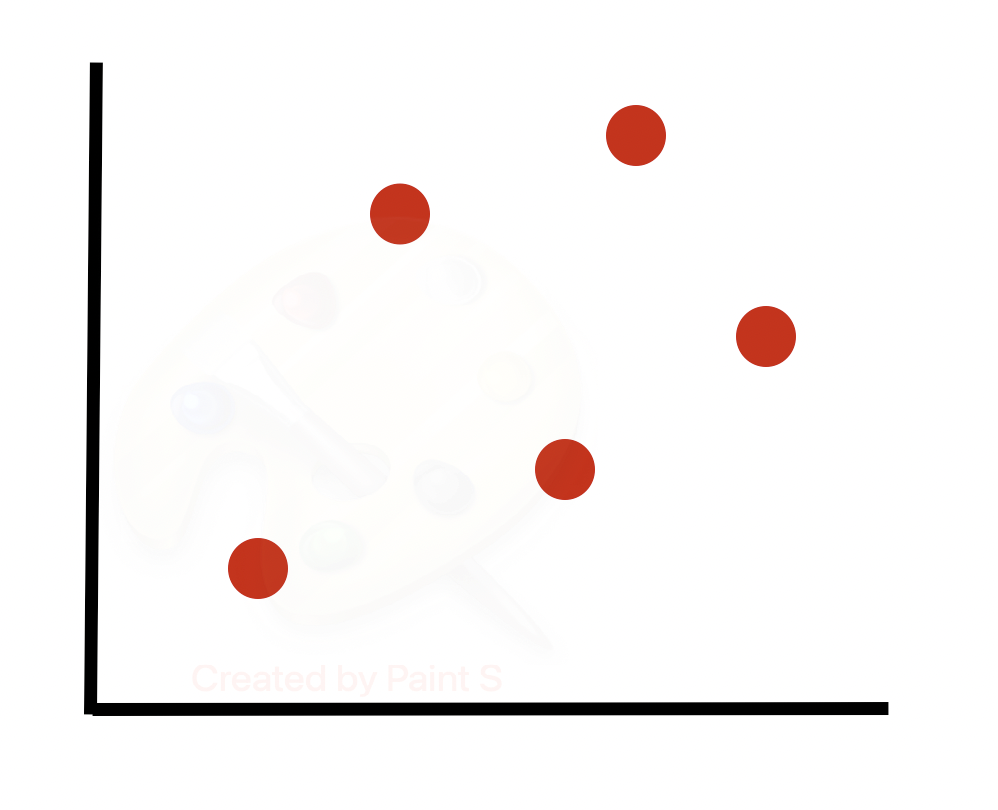
Берем первую строку (или случайную строку в случае N < 100) и вычисляем ее k-ближайших соседей. Затем выбираем случайного ближайшего соседа из k-ближайших соседей.

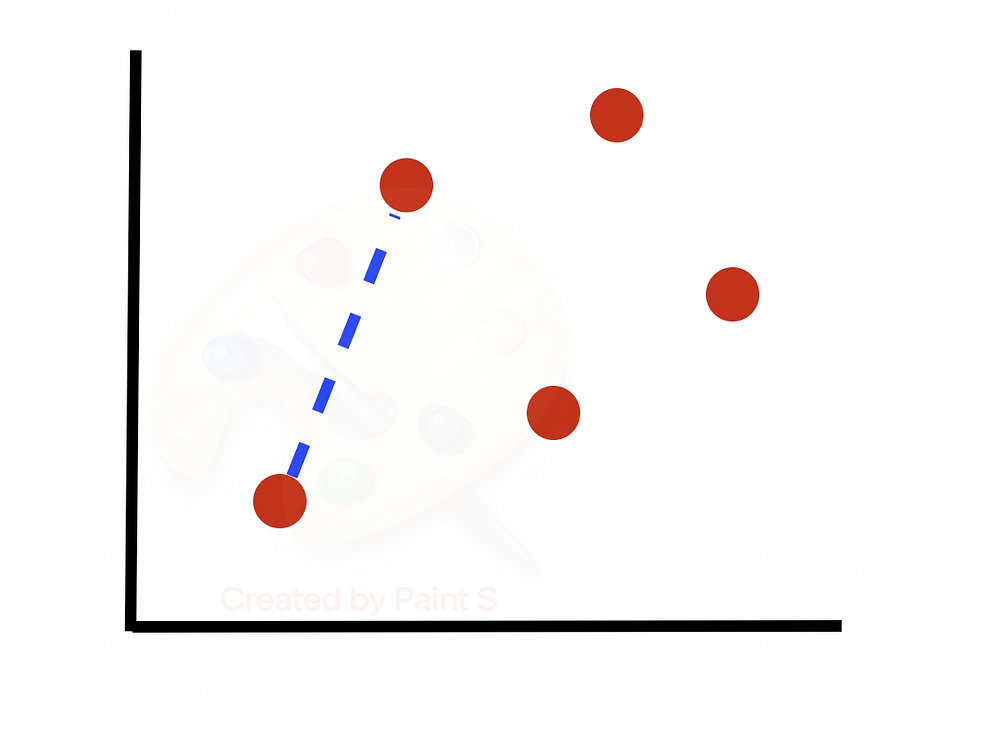
Вычисляем разность между двумя точками и умножаем ее на случайное число от 0 до 1. Получаем синтезированный образец вдоль линии между двумя точками.

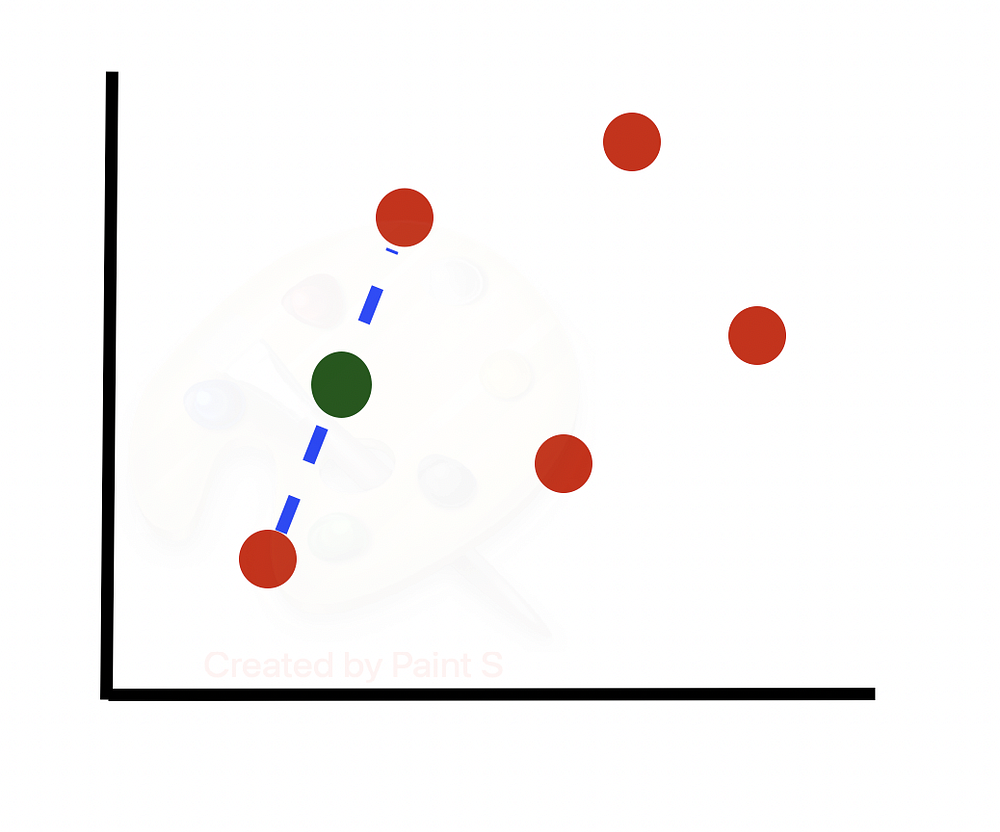
Повторяем этот процесс N/100 раз. Другими словами, если необходимый результат перевыборки составляет 300%, то из k = 5 ближайших соседей выбирается только 300/100 = 3 соседа и генерируется по одному образцу в направлении каждого из них. В этом случае задается N = 300. Таким образом, рассматривается 3 случайных ближайших соседа каждой точки.

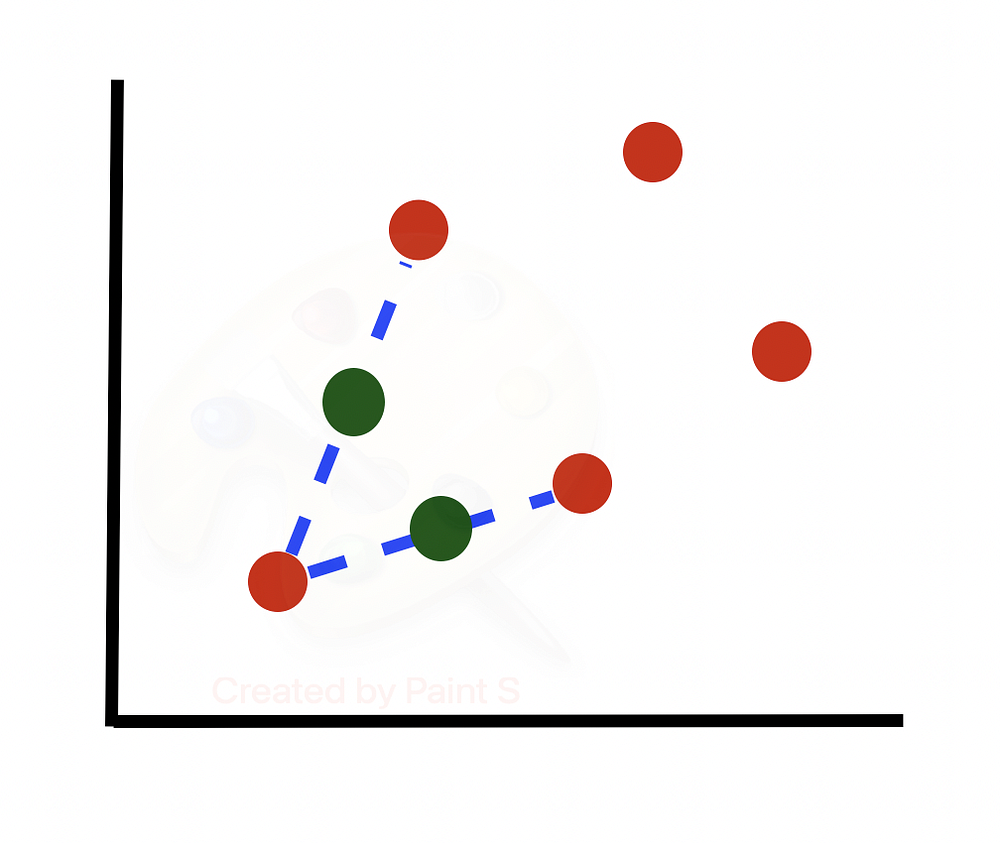
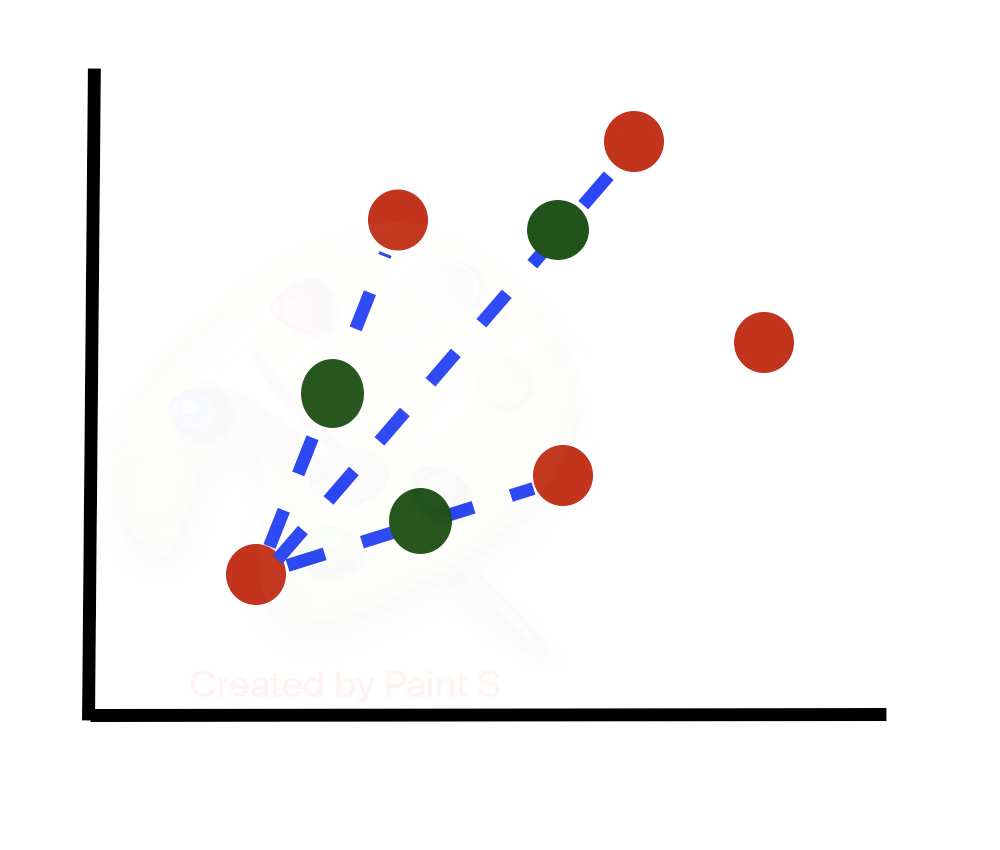
Затем переходим к следующей строке, вычисляем ее k-ближайших соседей и выбираем N/100 = 300/100 = 3 ближайших соседа случайным образом для использования в генерации новых синтезированных образцов.

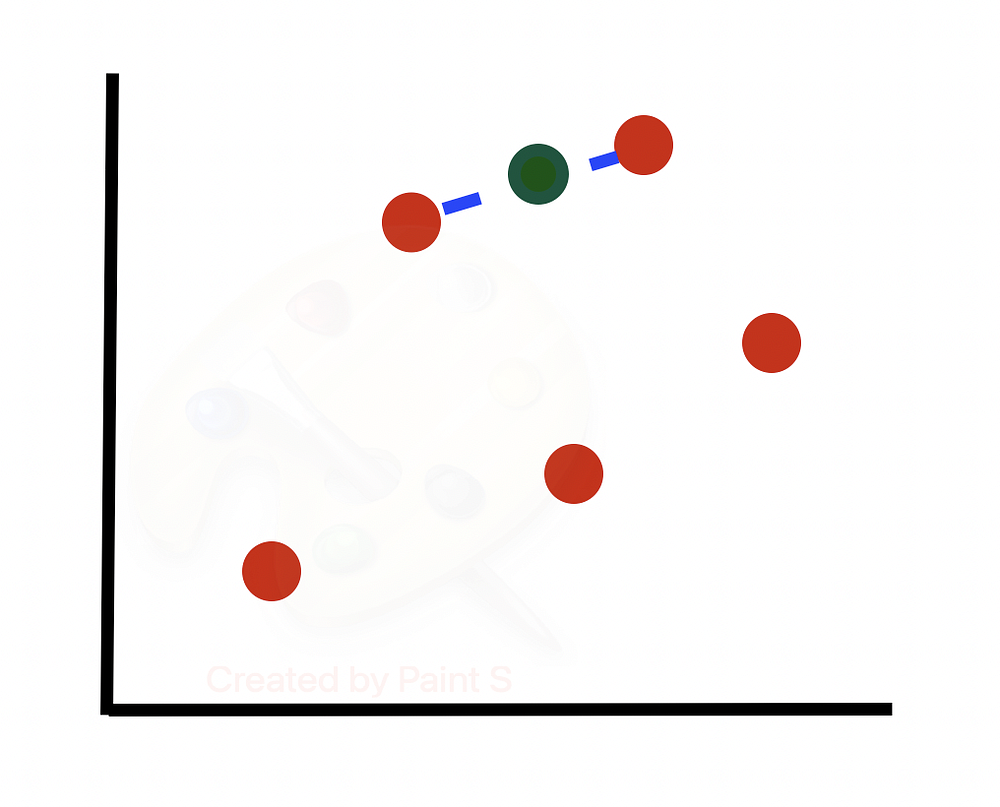
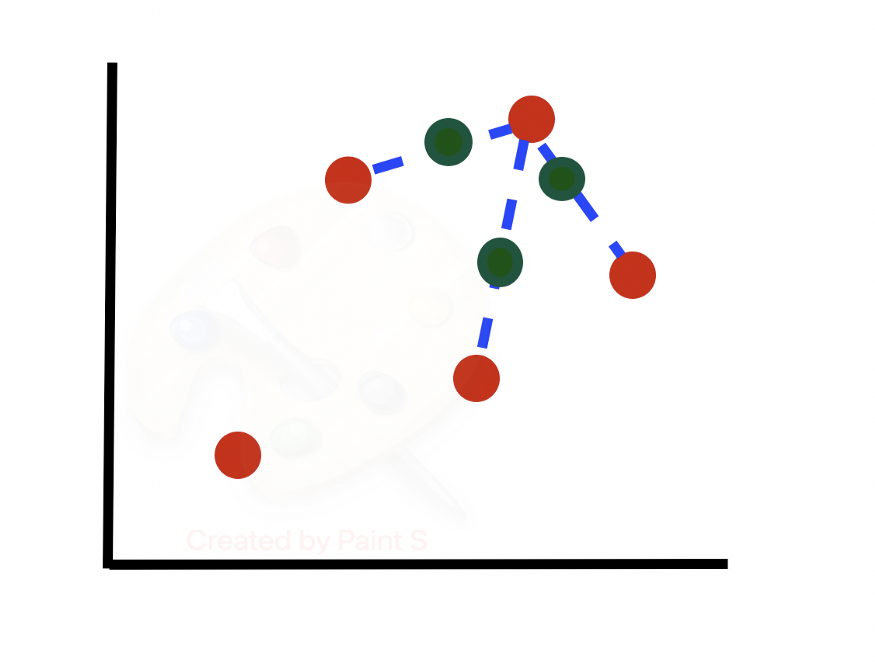
SMOTE в Python

Рассмотрим пример использования SMOTE в Python.

Начнем с импорта необходимых библиотек:

from random import randrange, uniform
from sklearn.neighbors import NearestNeighbors
import numpy as np
import pandas as pd
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix, recall_score

В этом примере воспользуемся набором данных Credit Card Fraud из Kaggle, чтобы обучить модель находить мошеннические транзакции. Считываем CSV-файл и сохраняем его содержимое в Pandas DataFrame следующим образом:

df = pd.read_csv("creditcard.csv")

К сожалению, из-за проблем с конфиденциальностью невозможно получить исходные признаки. Признаки V1, V2, … V28  —  это главные компоненты, полученные с помощью PCA. Признаки, которые не были преобразованы с помощью PCA  —  это “Время” (Time) и “Сумма” (Amount).

df.head(5)

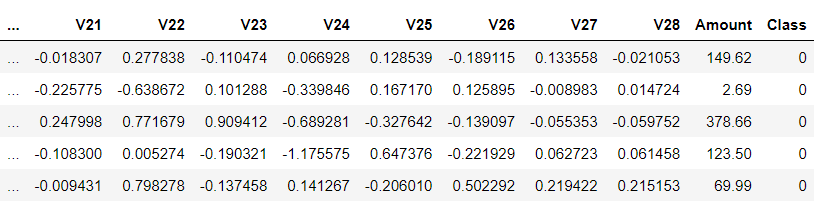
Как видим, отрицательных образцов значительно больше, чем положительных.

df['Class'].value_counts()

Out:
0    284315
1       492
Name: Class, dtype: int64

Для простоты удалим измерение времени:

df = df.drop(['Time'], axis=1)

Разделим набор данных на признаки и метки:

X = df.drop(['Class'], axis=1)
y = df['Class']

Чтобы оценить производительность модели, разделим данные на обучающий и тестовый наборы:

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

Далее инициализируем экземпляр класса RandomForestClassifier:

rf = RandomForestClassifier(random_state=42)

Подгоним модель под обучающее множество:

rf.fit(X_train, y_train)

Наконец, на основе того, что распознала модель, выясним, является ли транзакция мошеннической:

y_pred = rf.predict(X_test)

Предположим, что набор данных содержит 100 примеров мошеннических транзакций и 9900 примеров обычных.

Если в данном случае применить критерий точности для измерения эффективности модели, она могла бы достичь 99% точности, просто выдавая каждый раз результат false. Именно по этой причине будем использовать матрицу неточностей для оценки эффективности модели.

Как видим, модель классифицировала 23 образца как немошеннические, хотя на самом деле они были таковыми.

confusion_matrix(y_test, y_pred)

Out:
array([[56862,     2],
       [   23,    75]])

Для сравнения, если бы нужен был один показатель для оценки эффективности модели, можно было бы использовать отклик модели (recall). Напомним, что отклик модели равен количеству истинно положительных результатов, деленному на сумму истинно положительных и ложноотрицательных результатов.

recall_score(y_test, y_pred)

Out: 0.7653061224489796

Основы SMOTE

Алгоритм SMOTE был описан Нитешем Чавла и др. в техническом документе 2002 года под названием SMOTE: Synthetic Minority Over-sampling Technique. В этом документе приводится следующий псевдокод:

Переходим к реализации этого алгоритма в Python:

def SMOTE(sample: np.array, N: int, k: int) -> np.array:
    
    T, num_attrs = sample.shape
    
    # Если N меньше 100%, рандомизируйте выборки миноритарного класса, так как только случайный процент из них будет подвержен SMOTE
    if N < 100:
        T = round(N / 100 * T)
        N = 100
    # Предполагается, что результат SMOTE будет целочисленно кратен 100 
    N = int(N / 100)

synthetic = np.zeros([T * N, num_attrs])
    new_index = 0

nbrs = NearestNeighbors(n_neighbors=k+1).fit(sample.values)

def populate(N, i, nnarray):
        
        nonlocal new_index
        nonlocal synthetic
        nonlocal sample

while N != 0:
            nn = randrange(1, k+1)
            for attr in range(num_attrs):
                dif = sample.iloc[nnarray[nn]][attr] - sample.iloc[i][attr]
                gap = uniform(0, 1)
                synthetic[new_index][attr] = sample.iloc[i][attr] + gap * dif

            new_index += 1
            N = N - 1
    
    for i in range(T):
        nnarray = nbrs.kneighbors(sample.iloc[i].values.reshape(1, -1), return_distance=False)[0]
        populate(N, i, nnarray)
    
    return synthetic

Если данный код не совсем понятен, не расстраивайтесь. Разберем его пошагово.

Алгоритм предполагает, что если N > 100, то оно кратно 100. Если N <100, то выбираем подмножество образцов. Например, если N = 50 (например, 50%), то длина синтезированного массива должна быть 50 / 100 * T = 0,5T, где T  —  длина исходного массива строк, принадлежащих миноритарному классу. Здесь задаем N = 100, чтобы в последующей строке оно стало 1, поскольку надо создать синтезированную выборку, используя только 1 из ближайших соседей каждой точки в подмножестве.

    if N < 100:
        T = round(N / 100 * T)
        N = 100
    N = int(N / 100)

Здесь используем k+1, потому что реализация NearestNeighbors рассматривает саму точку как одного из соседей. Другими словами, наша цель  —  использовать метод k-ближайших соседей, исключив саму точку.

nbrs = NearestNeighbors(n_neighbors=k+1).fit(sample.values)

В Python nonlocal гарантирует, что переменная ссылается на “ближайшую” (в данном случае область видимости вне функции) переменную с тем же именем в исходном коде.

nonlocal new_index
nonlocal synthetic
nonlocal sample

Устанавливаем ближайшего соседа случайным образом, выбирая число от 1 до k+1, поскольку, как уже отмечалось, реализация NearestNeighbors рассматривает саму точку как одного из ближайших соседей:

nn = randrange(1, k+1)

Перебираем различные атрибуты в соответствии с алгоритмом, описанным выше. Однако стоит отметить, что существует более эффективный способ сделать это с помощью API NumPy.

for attr in range(num_attrs):

Создаем новый образец, взяв разность между рассматриваемой точкой и случайным соседом, затем умножаем ее на число от 0 до 1:

dif = sample.iloc[nnarray[nn]][attr] - sample.iloc[i][attr]
gap = uniform(0, 1)
synthetic[new_index][attr] = sample.iloc[i][attr] + gap * dif

Переходим к следующему доступному индексу в массиве и уменьшаем N, чтобы показать, что один из N/100 ближайших соседей уже учтен:

new_index += 1
N = N - 1

Получаем ближайших соседей для точки в исходном массиве и вызываем функцию populate:

for i in range(T):
        nnarray = nbrs.kneighbors(sample.iloc[i].values.reshape(1, -1), return_distance=False)[0]
        populate(N, i, nnarray)

Перед запуском алгоритма выбираем все строки с мошенническими транзакциями из набора данных:

minority = df[df['Class'] == 1].drop(['Class'], axis=1)

Задаем k равным 5. Это означает, что для каждой строки мы будем случайным образом выбирать N/100 ближайших соседей из имеющихся k = 5 для использования в расчетах (предполагается, что N ≥ 100). Задаем N = 200. Это означает, что необходимо сгенерировать на 200% больше примеров мошеннических транзакций:

synthetic = SMOTE(minority, N=200, k=5)

Как видим, массив синтезированных образцов имеет вдвое больше строк, чем исходный набор данных:

synthetic.shape

Out:
(984, 29)

Далее конкатенируем исходные образцы с только что сгенерированными образцами и устанавливаем метку на 1 для общего количества 984 + 492 = 1476 образцов.

synthetic_df = pd.DataFrame(synthetic, columns=minority.columns)
combined_minority_df = pd.concat([minority, synthetic_df])
combined_minority_df["Class"] = 1

Наконец, объединяем выборки с мошенническими и немошенническими транзакциями в один датафрейм:

new_df = pd.concat([combined_minority_df, df[df['Class'] == 0]])

Как и ранее, разбиваем данные на обучающий и тестовый наборы, обучаем модель и классифицируем строки в тестовом наборе:

X = new_df.drop(['Class'], axis=1)
y = new_df['Class']

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

rf = RandomForestClassifier(random_state=42)

rf.fit(X_train, y_train)

y_pred = rf.predict(X_test)

На матрице неточностей видно, что модель имеет такое же количество ложноотрицательных результатов несмотря на то, что положительных примеров стало в 3 раза больше.

confusion_matrix(y_test, y_pred)

Out:
array([[56844,     0],
       [   24,   291]])

Показатель отклика модели значительно выше, чем у той, что была обучена на наборе данных без использования SMOTE.

recall_score(y_test, y_pred)

0.9238095238095239

Использование библиотеки SMOTE

Python-реализация SMOTE доступна в его библиотеке (вне Scikit-Learn), которую можно установить следующим образом:

pip install imbalanced-learn

После этого можно импортировать класс SMOTE:

from imblearn.over_sampling import SMOTE

Чтобы избежать неточностей, снова прочитаем файл csv:

df = pd.read_csv("creditcard.csv")

df = df.drop(['Time'], axis=1)

X = df.drop(['Class'], axis=1)
y = df['Class']

Создаем экземпляр класса SMOTE. Стоит отметить, что по умолчанию он обеспечивает равное количество положительных и отрицательных выборок.

sm = SMOTE(random_state=42, k_neighbors=5)

Применим алгоритм SMOTE к набору данных следующим образом:

X_res, y_res = sm.fit_resample(X, y)

Снова разбиваем набор данных, обучаем модель и предсказываем, следует ли считать образцы в тестовом наборе данных мошенническими транзакциями или нет.

X_train, X_test, y_train, y_test = train_test_split(X_res, y_res, test_size=0.2, random_state=42)

rf = RandomForestClassifier(random_state=42)
rf.fit(X_train, y_train)

y_pred = rf.predict(X_test)

Взглянув на матрицу неточностей, увидим, что положительных примеров столько же, сколько и отрицательных, и у модели не было ни одного ложноотрицательного результата. Следовательно, отзыв равен 1.

confusion_matrix(y_test, y_pred)
Out:
array([[56737,    13],
       [    0, 56976]])

recall_score(y_test, y_pred)
Out: 1.0

Заключение

Когда модель машинного обучения обучается на несбалансированном наборе данных, она, как правило, работает плохо. Когда получение большего количества данных не представляется возможным, приходится прибегать к уменьшению или увеличению числа примеров. Первый подход плох тем, что удаляет образцы, которые могли бы быть использованы для обучения модели. Второй тоже не идеален, так как приводит к переобучению модели.

SMOTE позволяет увеличить количество примеров миноритарных классов, избегая при этом чрезмерного обучения. В результате создаются новые синтезированные образцы, близкие к другим точкам (принадлежащим к миноритарному классу) в пространстве признаков.

Читайте также:

• Лассо- и ридж-регрессии: интуитивное сравнение
• 19 скрытых фич Sklearn, о которых вам следует знать
• Гамма-функция - интуиция, определение, примеры

Читайте нас в Telegram, VK и Яндекс.Дзен

---

Перевод статьи Cory Maklin: Synthetic Minority Over-sampling TEchnique (SMOTE)