Выбор оптимального алгоритма поиска в Python

Когда дело касается обучения, мы, как правило, используем один из двух основных подходов: идём либо вширь и стараемся охватить как можно больший спектр области, либо вглубь и пытаемся получить конкретику в изучаемой нами теме. Преуспевающие в этом люди отмечают, что всё изучаемое нами в жизни, начиная от алгоритмов и заканчивая жизненными навыками, в определённой степени подразумевает совмещение этих подходов.

Здесь мы познакомимся с двумя основными алгоритмами поиска, а именно “поиском в глубину” (DFS) и “поиском в ширину” (BFS), которые лягут в основу понимания более сложных алгоритмов.

Содержание:

1. Обход дерева.
2. Поиск в глубину.
3. Поиск в ширину.
4. Сравнение предлагаемых алгоритмов.

Давайте начнём с обхода дерева.

Что вообще значит обойти дерево?

Поскольку деревья — это разновидность графа, их обход, иначе называемый поиск по дереву, является видом обхода графа. Тем не менее для дерева этот процесс отличается меньшей масштабностью.

Обход дерева обычно известен как проверка (посещение) или обновление каждого узла по одному разу без повторений. Поскольку все узлы связаны рёбрами, начинаем мы всегда с корневого. Это означает, что нельзя произвольно обратиться к любому узлу дерева.

К выполнению обхода существует три подхода:

• прямой;
• симметричный;
• обратный.

Прямой обход

В этом способе мы сначала считываем данные с корневого узла, затем перемещаемся к левому поддереву, а потом к правому. В связи с этим посещаемые нами узлы (а также вывод их данных) следуют тому же шаблону, в котором сначала мы выводим данные корневого узла, затем данные его левого поддерева, а затем правого.

Алгоритм:

Пока все узлы не будут посещены
Шаг 1 − Посещение корневого узла
Шаг 2 − Рекурсивный обход левого поддерева
Шаг 3 − Рекурсивный обход правого поддерева

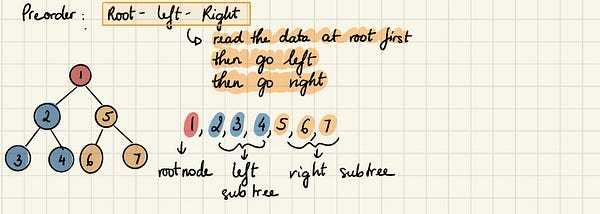
Мы начинаем с корневого узла и, следуя прямому порядку обхода, сначала посещаем сам этот узел, а затем переходим к его левому поддереву, которое обходим по тому же принципу. Это продолжается, пока все узлы не будут посещены. В итоге порядок вывода будет таким: 1,2,3,4,5,6,7.

Симметричный обход

При симметричном обходе мы проходим по пути к самому левому потомку, затем возвращаемся к корню, посещаем его и следуем к правому потомку.

Алгоритм:

Пока все узлы не будут посещены
Шаг 1 − Рекурсивный обход левого поддерева
Шаг 2 − Посещение корневого узла
Шаг 3 − Рекурсивный обход правого поддерева

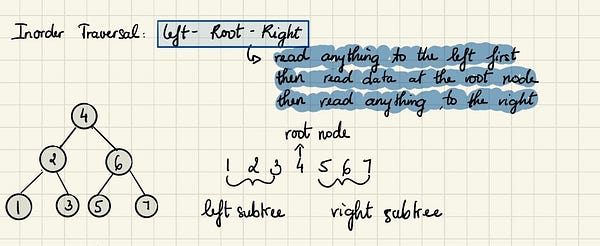
Начав от корневого узла 4, мы рекурсивно перебираем его левое поддерево, используя такой же симметричный порядок, затем посещаем сам корневой узел и далее перебираем правое поддерево.

Обратный обход

При обратном подходе мы сначала посещаем левого потомка, затем правого и по завершении обхода поддеревьев считываем корень. 

Алгоритм:

Пока все узлы не будут посещены
Шаг 1 − Рекурсивный обход левого поддерева
Шаг 2 − Рекурсивный обход правого поддерева
Шаг 3 − Посещение корневого узла

Становится ясно, что алгоритмы классифицируются на основе последовательности посещения узлов.

Здесь я снова упомяну, что есть две основных техники, которые мы можем использовать для обхода и посещения каждого узла исключительно по одному разу: поиск в глубину или поиск в ширину.

Поиск в глубину (DFS)

В этом способе мы всегда посещаем самый углублённый узел, затем идём назад и следуем другим путём, достигая другого конечного узла.

Обратите внимание, что в этом алгоритме для запоминания маршрута к конечному узлу и обратно используется механизм стека. 

При таком подходе нам нужно обойти всю ветку дерева и все прилегающие узлы. Поэтому для отслеживания текущего узла требуется подход “последним вошёл — первым вышел”, который реализуется через стек. После достижения самого глубокого узла все остальные узлы извлекаются из стека. Затем происходит обход прилегающих узлов, которые ещё не посещались. 

Если бы вместо стека использовалась очередь, представляющая подход “первым вошел — первым вышел”, то мы бы не смогли идти в глубину, не удаляя из очереди текущий узел. 

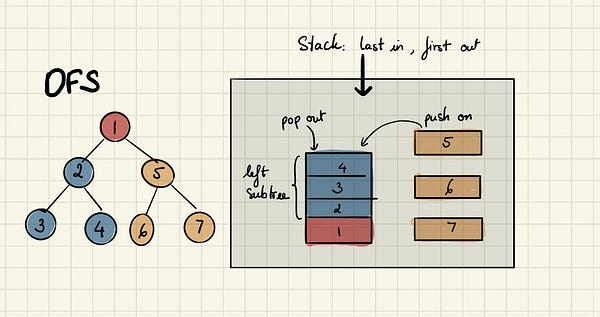
Здесь для наглядной демонстрации этого принципа мы используем простое бинарное дерево. Начиная от исходного узла А, мы двигаемся к смежному узлу B, а затем к D, где оказываемся в самом удалённой точке. Затем мы возвращаемся на шаг назад к B и переходим к следующему смежному узлу — E.

Давайте разобьём все наши действия на шаги. Сначала мы инициализируем стек и массив “visited” (посещённые узлы).

Добавляем корневой узел А в стек.

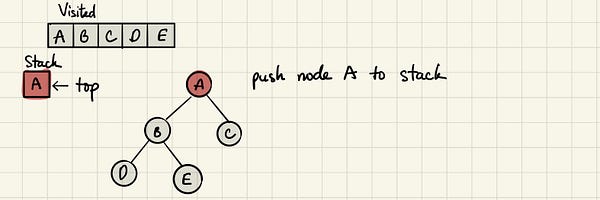
Помечаем узел A как посещённый и смотрим, есть ли среди смежных с ним узлов непосещённые. Есть два таких узла, помещаем их в стек и далее выбираем любой из них. Здесь будем следовать алфавитному порядку.

Помечаем B как посещённый и далее смотрим, есть ли у него соседи, которых мы ещё не посетили. Их два — D и E. Добавляем их в стек.

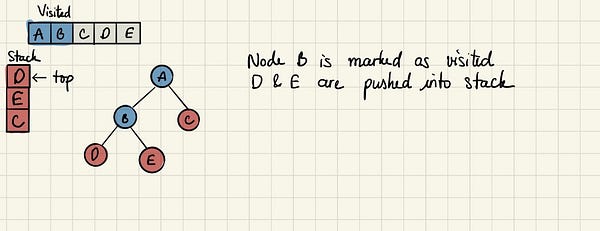
Посещаем D и отмечаем его. У этого узла нет непосещённых соседей, поэтому в стек ничего не добавляем.

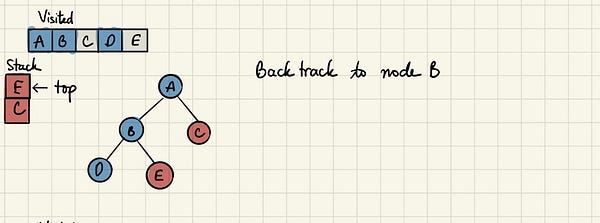
Проверяем верхушку стека и через возврат к предыдущему узлу посещаем E. Затем также проверяем наличие непосещённых соседей у него.

Поскольку таких соседей у этого узла нет, мы продолжаем освобождать стек, пока не найдём узел с новыми непосещёнными соседями. В этом случае такового нет, поэтому стек в итоге освобождается полностью.

Преимущества:

• DFS в отношении бинарного дерева обычно требует меньше памяти, чем BFS.
• DFS легко реализовать через рекурсию.

Недостатки:

• В отличие от поиска в ширину DFS не всегда находит ближайший путь к искомому узлу.

DFS в Python

Дерево в коде мы представляем, используя список смежности через словарь Python. Для каждой вершины есть список смежных ей узлов.

graph = {
    'A' : ['B','C'],
    'B' : ['D', 'E'],
    'C' : [],
    'D' : [],
    'E' : []
}

Далее мы определяем отслеживание посещённых узлов через инструкцию visited = set().

Взяв за основу список смежности и начав с узла A, мы можем найти все узлы дерева, применяя рекурсивную функцию DFS. Алгоритм функции dfs:

1. Проверяем, посещён ли текущий узел. Если да, то он добавляется в соответствующий набор.
2. Функция повторно вызывается для каждого соседа узла.
3. Базовый case вызывается, когда все узлы уже посещены, и после этого функция делает возврат. 

def dfs(visited, graph, node):
    if node not in visited:
        print (node)
        visited.add(node)
        for neighbor in graph[node]:
            dfs(visited, graph, neighbor)

Поиск в ширину (BFS)

В этом подходе мы выполняем поиск по всем узлам дерева, создавая широкую сеть. Это означает, что сначала мы обходим один уровень потомков и лишь затем переходим к последующему уровню уже их потомков.

Такой поиск сначала изучает ближайшие узлы и затем переходит всё дальше в сторону от исходной точки. С учётом этого мы хотим работать со структурой данных, которая при необходимости даёт самый старший элемент, считая их по порядку добавления. Здесь нам нужно применить механизм “очереди”.

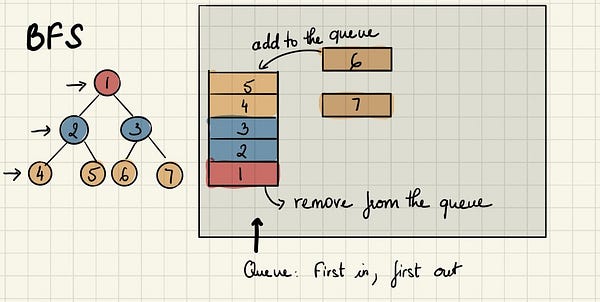
Посмотрим, как очереди помогут нам с реализацией BFS и увидим работу BFS в бинарном дереве. Начиная от исходного узла A, мы продолжаем по порядку исследовать ветки, а именно переходим сначала к B, а затем к C, на котором текущий уровень завершается. После мы спускаемся на следующий уровень и посещаем D, откуда следуем к E.

Сначала мы инициализируем очередь и массив “visited”.

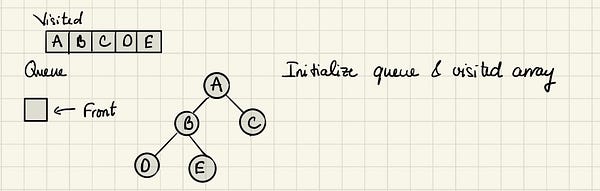
Начинаем с посещения корневого узла A.

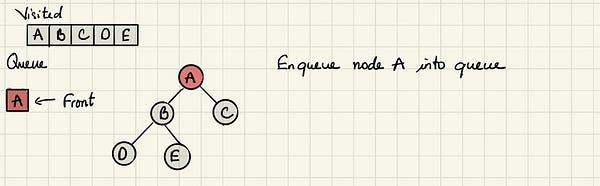
Отмечаем A как посещённый и переходим к смежным с ним непосещённым узлам. В данном примере это два узла — B и C, и мы добавляем их в очередь, следуя алфавитному порядку. 

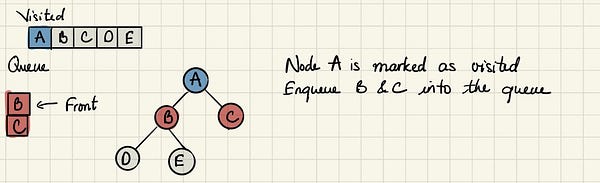
Далее мы отмечаем B как посещённый и добавляем в очередь его потомков — D и E.

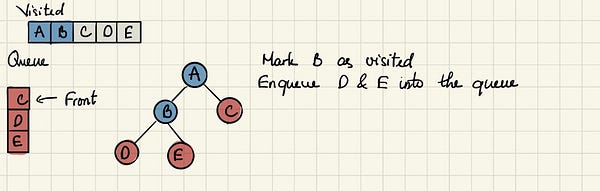
Теперь переходим к С, у которого нет непосещённых соседей. 

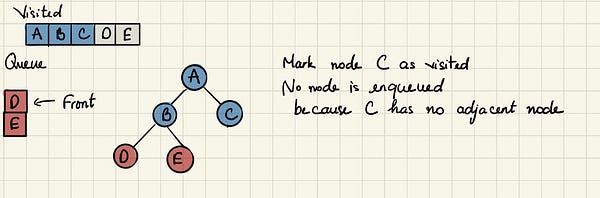
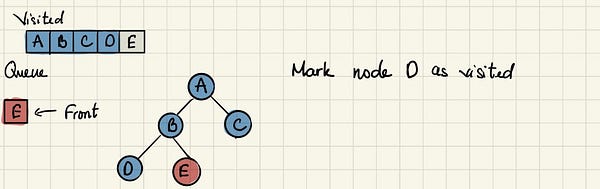
Далее, спустившись на уровень вниз, мы посещаем сначала D, а потом E, также продолжая убирать каждый посещаемый узел из очереди. Программа завершится, когда в очереди не останется элементов.

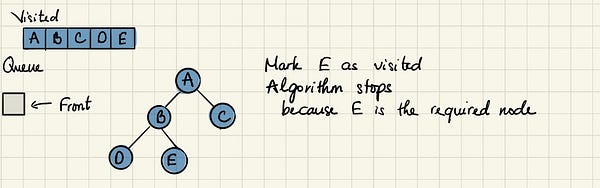
Преимущества:

• Легко реализовать.
• Можно применять в любой задаче поиска.
• В отличие от DFS не подвержен проблеме бесконечного цикла, которая может вызвать сбой компьютера при выполнении углублённого DFS-поиска.
• Всегда находит кратчайший путь при условии равного веса ссылок, в связи с чем считается полноценным и более оптимальным способом поиска.

Недостатки:

• BFS требует больше памяти.
• BFS — это так называемый “слепой” поиск, охватывающий огромную область, из-за чего производительность будет уступать другим аналогичным эвристическим методам.

BFS в Python

Дерево в коде мы также представляем, используя список смежности через словарь Python. Каждая вершина хранит список смежных с ней узлов. 

graph = {
  'A' : ['B','C'],
  'B' : ['D', 'E'],
  'C' : [],
  'D' : [],
  'E' : []
}

Далее для отслеживания посещённых узлов мы устанавливаем visited = [].

Для отслеживания узлов, находящихся в очереди, мы устанавливаем queue = [].

Учитывая список смежности и начиная от узла A, мы можем найти все узлы дерева, используя рекурсивную функцию bfs, которая:

1. Сначала проверяет и добавляет стартовый узел в список посещённых, а также в очередь. 
2. Далее, пока в очереди присутствуют элементы, она продолжает исключать узлы, добавлять их непосещённых соседей и затем отмечать их как посещённых.
3. Выполняет эти действия, пока очередь не опустеет.

def bfs(visited, graph, node):
    visited.append(node)
    queue.append(node)
    
    while queue:
        s = queue.pop(0) 
        print (s, end = " ") 
        
        for neighbor in graph[s]:
            if neighbor not in visited:
                visited.append(neighbor)
                queue.append(neighbor)

BFS или DFS?

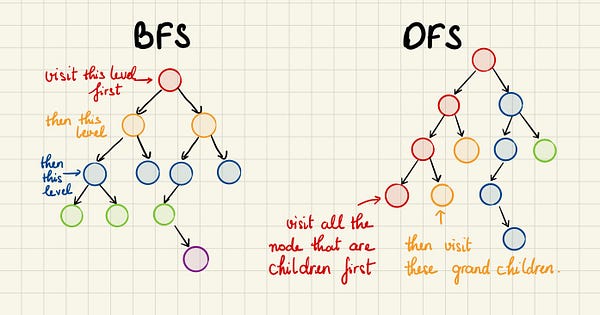
Вот мы и рассмотрели отличия DFS и BFS. Вам наверняка также интересно узнать, когда и какой из них подходит лучше. На ранней стадии изучения алгоритмов я тоже задавался этим вопросом. Надеюсь, мой ответ сможет дать достаточное пояснение:

• Если нам известно, что искомая точка находится недалеко от корня, то лучше использовать BFS.
• Если дерево имеет очень глубокую структуру, а искомые точки в нём редки, то DFS может потребовать очень много времени. BFS же справится быстрее.
• Если дерево очень широкое, то BFS может потребовать так много памяти, что утратит свою практичность. 
• Если искомые точки встречаются часто, но расположены в глубине дерева, BFS может также оказаться непрактичным.

Обычно стоит использовать:

• BFS, когда нужно найти кратчайший путь от конкретного исходного узла к нужной точке. Иначе говоря, когда нас интересует путь с наименьшим числом шагов, ведущих от заданного начального состояния к искомому.
• DFS, когда нужно исследовать все возможности и найти наилучшую либо пересчитать количество возможных путей. 
• BFS или DFS, когда нужно только проверить наличие связи между двумя узлами представленного графа или, иначе говоря, узнать, можем ли мы достичь одного, находясь в другом.

Вот и всё!

Мы изучили теорию и разобрались в двух популярных алгоритмах поиска — DFS и BFS. Помимо этого, теперь вы знаете, как реализовывать их в Python. Настало время применить все эти знания на практике. Не стоит откладывать, ведь это занятие будет уже куда интереснее чтения. Код BFS и DFS доступен на GitHub.

Читайте также:

• Почему мы создали платформу для инженерии машинного обучения, а не науки о данных
• 5 секретов наилучшего использования кортежей в Python
• Утиная типизация в Python - 3 примера

Читайте нас в Telegram, VK и Яндекс.Дзен

---

Перевод статьи XuanKhanh Nguyen: Depth-First Search vs. Breadth-First Search in PythonDepth-First Search vs. Breadth-First Search in Python