Злые единицы - добрый Frink

Введение

Единица измерения  —  это физическое свойство, представляющее собой число, например, расстояние или время. Мы почти всегда говорим о системе единиц СИ.

У единиц могут быть экспоненты: м² — квадратные метры, м³ — кубические метры, m/s для скорости. Они формируют новые физические свойства, или меры. Мы можем умножать и делить числа с разными свойствами, но не складывать их: 1м + 1м, но не 1м + 1кг. Язык, учитывающий это, должен отслеживать свойства, а также следить за тем, чтобы несовместимое не складывалось. Он также должен гарантировать, что передаются корректные единицы в зависящие от них функции. При расчете давления необходимо учитывать площадь и силу, но не частоту и силу тока. Просто, да?

Нет

Прежде всего, множество представлений единиц огромно. Есть система СИ, которую используют все здравомыслящие, праведно мыслящие народы, а есть американская система. Вините Рональда Рейгана. Метрификация в США должна была завершиться к 90-м, но Рейган убил программу.

Продолжим. Футы и метры  —  это расстояния. Можно ли смешивать футы и метры, не конвертируя величины? Такое смешивание  — причина бага, уничтожившего Mars Climate Orbiter. Но есть и корректные случаи складывания. Представим некоторую миссис Смит из США, которая готовит пирог: она будет пользоваться разными весами и американскими объемами, например, 1 стакан воды и 128 граммов муки. В Великобритании пиво измеряется пинтами, а объём другого алкоголя измеряется единицами СИ.

Разные меры не всегда несовместимы. В некоторых нишах физики используется нестандартный набор единиц под названием “гауссовские единицы”. В СИ ёмкость измеряется в Фарадеях: A² s⁴/(kg*m*m). В гауссовых единицах ёмкость измеряется кубических сантиметрах. Если вы прямо говорите о том, что делаете, вы можете складывать эти, казалось бы, несовместимые единицы.

Единицы неуникальны, то есть две несовместимые физические величины могут иметь одно и то же измерение. Канонический пример: энергия и угловая сила измеряются в ньютон-метрах. Это не точно одинаковые меры: энергия — скаляр, а крутящий момент — вектор. Но векторные составляющие крутящего момента имеют одинаковые меры и они скаляры. Есть множество примеров из конкретной области. При входе в гравитационный колодец скорость, при которой изменяется сила гравитации, измеряется в N/m. Поверхностное натяжение также измеряется в N/m.

Что ещё?

• Как насчёт 200° + 360°? Получается 200° или 560°, в зависимости от того, круглый у нас угол или угол вращения (как при ввинчивании винта).
• Некоторые количества без единиц измерения. Что такое 20° + 1 радиан? У обоих совместимые меры. Как насчет сложения двух соотношений? Или сложение радиана и соотношения?
• Единицы могут иметь дополнительные ограничения: временные метки можно вычитать, но складывать их нельзя.
• Они также могут иметь разные исторические значения. Фут — это 0,3048 метра. До 1959 года, однако, он был 0,3048006 метра. Кроме того, был период времени, когда мы использовали оба определения в разных местах!
• Неопределенности. Если вы работаете с физическими измерениями, все они будут в некоторой степени неопределенными. Что случится, если добавить два метра плюс-минус сантиметр?

Если вы хотите узнать больше о том, что такое злые единицы, обратитесь к отчёту Билла Кента об измерениях.

Некоторые решения

Добавление единиц измерения к языку — сложная задача. Дело не только в том, что существует много сложных проблем в области, но и в различных компромиссах в решениях. Нам нужна корректность времени компиляции или выполнения? Должны ли единицы быть частью системы типов или существует лучшее представление? Как мы обращаемся с производными единицами? С дженериками? Хороший обзор проблем, связанных с проектированием, представлен здесь. Там обсуждаются некоторые из решений, предложенных для языка Ada.

Эта страница рассказывает о том, как различные языки подходят к измерениям. По большей части они обращаются к препроцессорам и библиотекам, ограничивая этим свою помощь. Единственный распространённый язык со встроенной поддержкой единиц измерения —  F#. Он фокусируется на отлавливании всех ошибок во время компиляции. Все преобразования между блоками должны быть чёткими, так что вы не можете случайно сложить фут и метр. Цена этого  —  гибкость. Я повторю: вы не сможете сложить сантиметры и метры.

// Масса, граммы.
[<Measure>] type g
// Масса, килограммы.
[<Measure>] type kg
​
// Определяем константы преобразования.
let gramsPerKilogram : float<g kg^-1> = 1000.0<g/kg>
​
// Определяем функции преобразования.
let convertGramsToKilograms (x : float<g>) = x / gramsPerKilogram

Язык добавляет шаблон, не давая программе стать непрочной. Это хорошо для промышленного ПО, где ошибка может повлиять на многих людей. Но меньше подходит для низкооплачиваемой, мелкомасштабной работы. Бойлерплейт затрудняет применение в интерактивном режиме. Если нужно найти вес “Титаника” в чашках риса, то нет необходимости тратить десять минут на конверсию величин. Распространённый инструмент для таких целей  —  units, программа GNU для преобразования:

You have: 12 ft + 3 in + 3|8 in
You want: ft
        * 12.28125
        / 0.081424936

units – прекрасный инструмент, но это не язык программирования. Если нужен язык, который имеет встроенный анализ измерений без большого количества бойлерплейта, то выбор стоит за чем-то мощнее units, но мягче F#.

Frink

И это нечто  —  Frink. Во Frink любое число может быть единицей измерения. Язык предотвращает сложение несовместимых единиц, как и F#.

> 1 meter
1 m (length)
​
> 1 meter + 2 kilograms
Error when adding:  meter + 2 kilograms
 Cause: Conformance Exception:
 Cannot add units with different dimensions.
  Dimension types:
   m (length)
   kg (mass)

Идея синтаксиса в том, чтобы код выглядел естественной математикой, поэтому пробел означает умножение. 1 метр — это на самом деле 1 * метр. Может показаться, что это вызовет некоторые проблемы, но на самом деле такой подход приятен и облегчает описание уравнений на Frink.

Оператор -> преобразует значение между двумя единицами. Мы можем выбрать, включать ли имя единицы в конвертацию или нет, поместив его в кавычки:

> 10 meters + 2 furlongs -> "feet"
2029212500/1499997 (approx. 1352.8110389554112) feet

У Frink на борту есть заранее определённые единицы: unit file длиной более 5000 строк:

// как вы измеряете, о мера года?
> 525600 minutes -> years
0.99933688171353600106
​
> 525600 minutes -> siderealyears
0.9992981356527034257
​
> 525600 minutes -> gaussianyears
0.99926355644744010579
​
> 525600 minutes -> calendaryear
1

Во время выполнения можно определить новые единицы в терминах существующих:

> corn_on_sale := 0.25 USD
// Живя на прожиточный минимум, сколько 
// можно купить кукурузы за рабочий день?
> 15 USD/hour * 8 hours -> "corn_on_sale"
480. corn_on_sale
​
> 15 USD/hour -> "corn_on_sale/(8 hours)"
480.0 corn_on_sale/(8 hours)

Префиксы во Frink  —  это множители и больше ничего. Я могу написать kilofoot и язык понимает, что это 1000 футов. Frink также понимает такие распространенные термины, как половина и квадрат.

> square megapaces
5.80644e+11 m^2 (area)

Вы можете разбить преобразования на несколько единиц.

> 1 kilometer -> ["kilofeet", "feet", "inches"] 
3 kilofeet, 280 feet, 1280/127 (approx. 10.078740157480315) inches
​
> 1 kilometer -> ["kilofeet", "feet", "inches", 0]
3 kilofeet, 280 feet, 10 inches

Функции Frink работают так, как вы ожидаете, но вы заставляете параметры соответствовать мерам и предусловиям.

> sphereVolume[radius is length] := 4/3 pi radius^3 
​
> sphereVolume[2]
Error when calling function sphereVolume:
  Constraint not met--value must have dimensions of length

Функции также могут быть целью преобразования.

> HMS[1 day]
24 hours, 0 min, 0 sec
​
> (10 miles) / (3 mph) -> HMS
3 hours, 20 min, 0 sec

Возможности

Frink блестяще справляется. В нём много мелочей, помогающих в интерактивном применении. Несколько примеров: изменяем единицы измерения дисплея:

> length :-> [feet, inches, 0]
​
// Все длины теперь в футах и ​​дюймах
> 1 meter
3, 3
​
// площадь не затронута
> 2 m * 2 m
4 m^2 (area)

Возможно глобально настроить точность и форматы вывода:

> setPrecision[6]
 
> setEngineering[true]
​
140.5 million meters
140.500e+6 m (length)

Или определить совершенно новые меры и префиксы:

> population =!= person
> 2.7 megaperson / (5 square miles) -> (square feet) / person
Warning: reciprocal conversion
51.626666666666666665

Введя ?str, вы получите список всех существующих мер, начинающихся со str. Прибавление к названию ?? выведет также значения мер:

> ?foot
[acrefoot, arabicfoot, assyrianfoot, boardfoot, cordfoot, doricfoot, earlyromanfoot, foot, footballfield, footcandle, footlambert, frenchfoot, greekfoot, ionicfoot, irishfoot, lateromanfoot, northernfoot, olympicfoot, romanfoot, scotsfoot, sumerianfoot, timberfoot]
​
> ??foot
arabicfoot = 0.270256 m (length)
assyrianfoot = 0.27432 m (length)
boardfoot = 18435447/7812500000 (exactly 0.002359737216) m^3 (volume)
// строк больше

Есть специальный синтаксис представления временных меток, позволяющий легко конвертировать даты и время.

// Встреча завтра, 15:00 по парижскому времени, сколько это в Нью-Йорке?
> # 3 PM Paris # + 1 day-> "New York"
AD 2020-07-10 AM 09:00:00.000 (Fri) Eastern Daylight Time

Примеры применения

Элиасен любит готовить, поэтому у Frink есть множество мер для еды. Многие рецепты выпечки требуют объема “просеянной муки”, но просеивание грязное, раздражающее и неточное. Лучше измерить массу:

> ?flour
[breadflour_scooped, breadflour_sifted, breadflour_spooned, 
cakeflour_scooped, cakeflour_sifted, cakeflour_spooned, 
flour_scooped, flour_sifted, flour_spooned]
​
> 2.5 cups flour_sifted -> grams
283.49523125

Сделаем что-то посложнее. Я тоже люблю готовить. В основном я готовлю пикантные блюда, а также люблю конфеты. Мне всегда было немного любопытно, сколько калорий в одной конфете. Разберёмся в этом с помощью Frink.

Для этого примера я воспользуюсь рецептом чая “Чай” из книги CIA. Нет, не ЦРУ, а другое CIA:

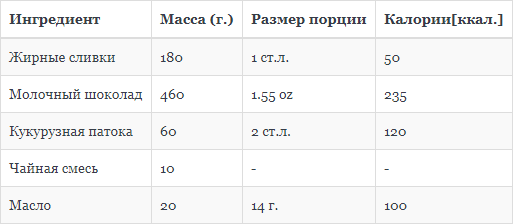
Я прочитал калории ингредиентов на этикетке, за исключением молочного шоколада. Но нашёл информацию в Интернете, здесь.

> specific_energy :-> "kcal/gram"
> energy :-> "kcal"

:- > изменяет представление единицы измерения по умолчанию. Без него удельная энергия была бы представлена в базовых единицах СИ, джоулях на килограмм. Затем я поместил все измерения в словари. Я не стал переводить каждую меру в единицы СИ потому, что Frink может вычислить соотношения.

kcg = new dict // kcal/gram
kcg@"hc" = 50 kcal / (tablespoon heavycream)
kcg@"cs" = 120 kcal / (2 tablespoon cornsyrup)
kcg@"butter" = 100 kcal / (14 grams)
kcg@"mc" = 235 kcal / (1.55 oz)
​
recipe = new dict //what actually goes in
recipe@"hc" = 180 grams
recipe@"cs" = 60 grams
recipe@"mc" = 460 grams
recipe@"butter" = 20 grams
​
ing = ["hc", "cs", "mc", "butter"]
​
total_cals = 0 kcal
for x = ing
  total_cals = total_cals + recipe@x kcg@x

В зависимости от покрытия, этого достаточно для 80–100 шоколадных конфет. Отразим неопределенность интервалом:

made = new interval[100, 120]

Вся математика с интервалом меняет границы. Frink рассматривает интервалы как одно неизвестное значение внутри интервала, а не как сам диапазон. Это означает, что для любого интервала x верно равенство x - x = 0.

> x = new interval[80, 100]
[80, 100]
​
// интервальная математика
> x + 2
[82, 102]
​
> x * 2
[160, 200]
​
> x - new interval[80, 100]
[-20, 20]

Конфета  —  это не только начинка. У глазури иная удельная энергия, чем у наполнителя. Чтобы выяснить, сколько покрытия нужно на одну конфету, я взвесил 10 шоколадных конфет и взял среднее. Получилось 9 граммов. Я знаю приблизительно, сколько начинки нужно на конфету исходя из того, сколько вообще сделано. Вычитание массы начинки из массы всего шоколада, конечно же, даст массу глазури:

dictsum[d] := sum[map[{|x| x@1}, d]]
​
// граммов на конфету
gpc = new dict
gpc@"recipe" = dictsum[recipe] / made
gpc@"dc" = 9 grams - gpc@"recipe"

С этого момента вычисляется простое количество калорий как в глазури, так и в наполнителе:

println[(total_cals / made)  + kcg@"mc" * gpc@"dc"]

Итак, одна конфета  —  это 40–50 ккал. Как я и ожидал.

Если Frink вас заинтересовал, то можете скачать его здесь. По крайней мере, я бы рекомендовал посмотреть на файл единиц по умолчанию. Этот файл  —  уморительное, проницательное введение в то, какими странными бывают меры. Просто оставлю несколько комментариев о канделе:

Я думаю, кандела  —  это афера, и я категорически против неё. Некоторые никчёмные “инженеры” или психологи по свету, наверное, втянули эту омерзительную идею в научную деятельность. Какая невероятно бесполезная и глупая мера. Является ли свет при 540.00000001 x 10¹² Гц (или любой другой частоте) нулевой канделой? Ожидается ли на такой частоте импульсная функция? Подождите, принцип неопределенности Гейзенберга делает такое невозможным. Нет упоминания о коррекции (в идеале вдоль кривой черного тела) для других длин волн? Гори в аду, 16 CGPM! Горите вы все в аду!

Читайте также:

• Уведомления о контактах
• Шаблон проектирования прототипов в современном C++
• Углубление в параметры ядра. Часть 1: загрузочные параметры

---

Перевод статьи Hillel Wayne: The Frink is good, the unit is evil.