3 случая, когда линейная модель может ошибаться

Введение

В этой статье я покажу три случая, когда линейные модели могут привести к неверным результатам. Основное внимание будет уделено сравнению линейных моделей с моделируемыми данными и проверке соответствия итоговых значений исходным данным.

Код для воспроизведения полученных в статье результатов можно найти на GitHub.

Общие сведения

Пусть Y — это то, что необходимо смоделировать. Предположим, нам известно, что Y определяется вектором переменных X как Y = β X, где β — вектор параметров, по одному на каждую из переменных X.

Ожидается, что линейная модель укажет верные значения β, так как между Y и X существует линейная зависимость.

Мы рассмотрим 3 случая, когда это условие не работает из-за наличия искажающих переменных.

Случай 1

Допустим, у нас есть три случайные переменные X, Y и Z, зависимость между которыми определяется так:

На Рисунке 1 видно, что X и Y исходят из Z и независимы друг от друга.

Вот как выглядел бы набор данных, основанный на Рисунке 1:

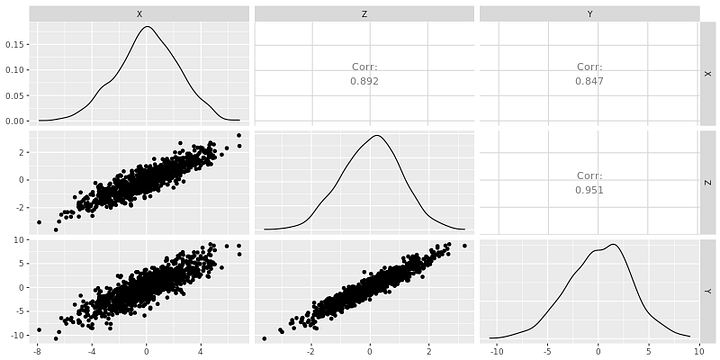
Чтобы сгенерировать набор данных на Рисунке 2, использовался следующий код:

Заметьте, что Y = 3 Z (плюс кое-какие случайные помехи), а вовсе не функция от X.

Представим, что нам нужно найти факторы, влияющие на Y, а всё, что у нас есть, это X. Ниже результат регрессии Y по X:

К удивлению, мы получаем статистически достоверный результат и делаем ошибочный вывод, что X влияет на Y, а Y = 1,18 X.

А теперь представим, что мы собрали больше данных, и теперь у нас есть и Z тоже. Регрессия Y по X и Z даёт следующий результат:

Итог соответствует моделируемым данным — между X и Y нет взаимозависимости, Y = 3 Z.

Данный пример даёт основания предположить, что добавление переменных в модель линейной регрессии всегда целесообразно, поскольку позволяет линейной модели правильно определять взаимозависимости при верных значениях переменных. Следующий случай докажет обратное.

Случай 2

Ниже представлен набор данных, где зависимость между X и Y такова: Y = 5,5 + 4,0 X.

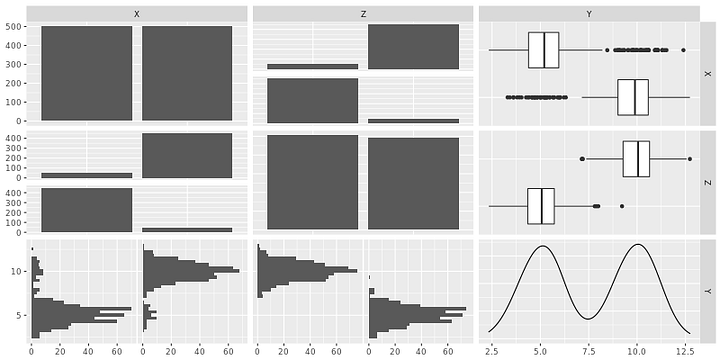
Отметим, что X и Z — бинарные переменные (0 или 1).

На Рисунке 6 чётко прослеживается сильная взаимозависимость между X и Y, а также между Y и Z.

Если бы мы не знали, как в действительности связаны между собой эти три переменные (что в реальном мире случается часто), нам захотелось бы включить эти две переменные в нашу модель. И вот что получилось бы:

Согласно Рисунку 7, зависимости между X и Y нет, а Y = 10–5 Z.

Но если вычислить регрессию Y по X, получим:

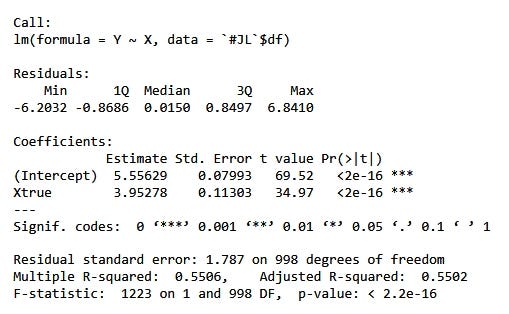
Результат совпадает с параметрами, используемыми для моделирования данных!

Таким образом, в Случае 1 регрессия Y по X даёт неверный результат, а в Случае 2 — верный. Откуда разница?

Разница появляется из-за взаимозависимости X, Y, Z. В Случае 2 зависимость между этими тремя переменными такая:

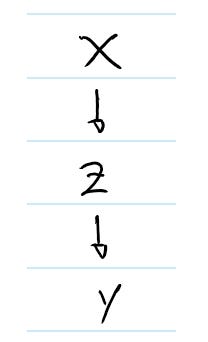
Из Рисунка 9 следует, что Z исходит из X, а Y исходит из Z. Противопоставьте это Рисунку 1, где указано, что X и Y исходят из Z.

Перед тем, как сделать окончательные выводы, рассмотрим третий случай.

Случай 3

Рассмотрим следующий набор данных:

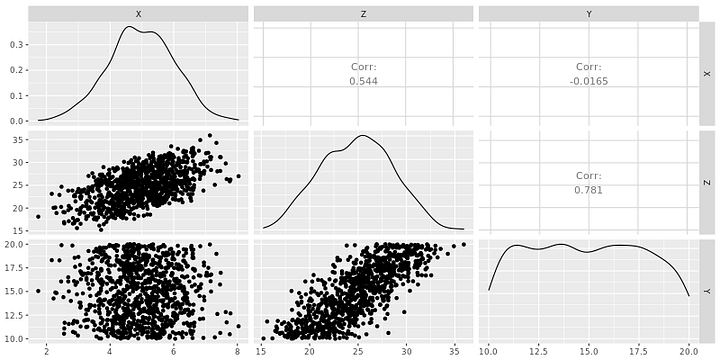
Здесь ясно видно, что X и Y независимы друг от друга. Если бы мы упустили эту деталь из виду и продолжили вычисление регрессии Y по X и Z, то получили бы:

Мы решили бы, что между X и Y есть взаимозависимость, что является ошибкой.

Причина кроется в том, что зависимость между X, Y и Z в наборе данных была следующей:

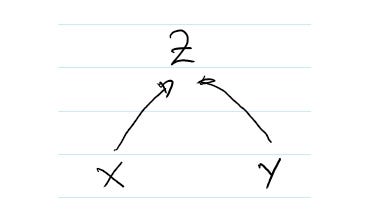
Согласно Рисунку 12, Z исходит из X и Y, а именно — Z в наборе данных относится к X и Y как Z = 2 X + Y.

Таким образом, если нам известны X и Z, то мы определённо знаем что-то и об Y. Но пытаться изменить Y, меняя X, в данном случае бессмысленно.

Выводы

Вот идеи, которые я выделил, исходя из рассмотренных моделей:

1. Если ваша единственная цель — создание точного прогноза, то можете спокойно включать в вашу модель все переменные, какие только сможете собрать, при условии, что они будут доступны и на этапе заключительного анализа.
2. Если вы планируете использовать выводные данные модели, вам нужно быть осторожными с выбором переменных для включения в модель. К примеру, если X — рекламная кампания, Z — трафик сайта, а Y — доход, то для оценки эффективности рекламной кампании вычислять регрессию Y по X и Z было бы неверно, полагая, что Z исходит из X, а Y исходит из Z (см. Случай 2).

Так как же выбрать правильные переменные для моделирования X и Y?

Один из способов — обратиться к специалистам в предметной области и узнать, каким образом другие переменные могут влиять на X и Y, и составить график, описывающий эти взаимозависимости. Затем к этому графику нужно применить “секретное условие”, позволяющее определить минимальный набор переменных, необходимых для объективной оценки влияния X на Y.

Заключение

В этой статье я показал 3 случая, когда линейная модель может дать неправильные, но статистически достоверные результаты.

Стоит отметить, что эти 3 взаимозависимости могут объединяться в более сложные конструкции. Это повышает вероятность случайно включить в модель переменные, использование которых приведёт к неверной оценке влияния X на Y.

Читайте также:

• Значение Data Science в современном мире
• Шесть рекомендаций для начинающих специалистов по Data Science
• Почему за способностью объяснения модели стоит будущее Data Science

---

Перевод статьи ___: 3 Ways Linear Models Can Lead to Erroneous Conclusions