Задача
Предположим, у нас есть крупная база данных из N элементов. Мы хотим найти один из элементов, например p, по ID, скажем w. Используя классические вычисления, нужно было бы проверить около N/2 элементов, чтобы найти совпадение с w, а в худшем случае и все N. Однако, используя алгоритм Гровера, можно найти w за √N шагов, а это квадратичное ускорение.
Оракул
Один из способов найти w — создать функцию f, возвращающую 0, если ID не совпадает с w, и 1, если совпадает. Далее определяем матрицу оракула U_f (где _ означает нижний индекс), чтобы действовать на основании состояний |x⟩:
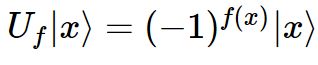
Таким образом, когда f(x) возвращает 0 (что означает, x не совпадает с w), -1 для f(x) становится 1. Когда f(x) возвращает 1 (что означает, x совпадает с w), -1 для f(x) становится -1. Следовательно, если x не является p, оракул ничего не делает. Если x равен w, он отображает |w⟩ в -|w⟩. Геометрически эта унитарная матрица соответствует отражению исходной для элемента w в N-мерном векторном пространстве.
Амплитудное усиление
Пока мы не видим список элементов, у нас нет предположений о том, где находится помеченный элемент, следовательно любая догадка о его местоположении одинаково хороша. Такая равномерная суперпозиция вероятности выражается как:
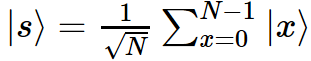
Если в любой точке x будет измерен, в соответствии с пятым принципом квантовой механики (известным также как правило Борна) суперпозиция коллапсирует до одного из базовых состояний с одинаковой вероятностью 1/N.
Амплитудное усиление, как видно из названия, усиливает вероятность выбранных элементов, соответственно ослабляя вероятность других (сумма квадратов всех вероятностей должна добавляться к 1).
Два пути визуализации процесса
Процесс как вероятности
Шаг 1: Процедура начинается в равномерной суперпозиции |s⟩. Пунктирная линия — это средняя амплитуда. Розовый блок — это p. Диаграмма в случае N = 4.
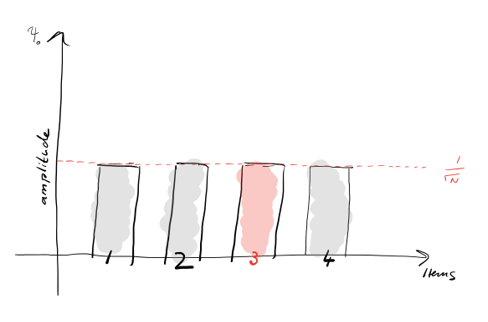
Шаг 2: Применяем отражение оракула U_f к состоянию |s⟩, перевернув его отрицательно. Заметьте, что средняя амплитуда уменьшилась.
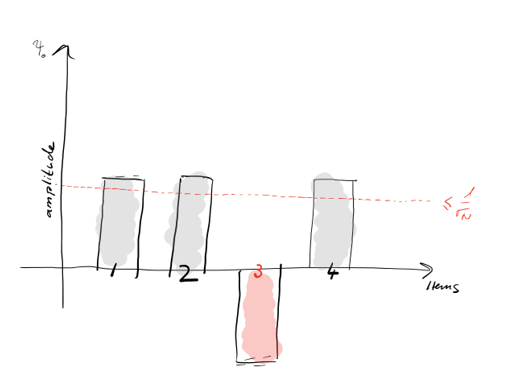
Шаг 3: Применяем отражение приближённо к состоянию |s⟩ (средняя амплитуда). Это завершает преобразование, увеличивая P и соответственно уменьшая остальные элементы.
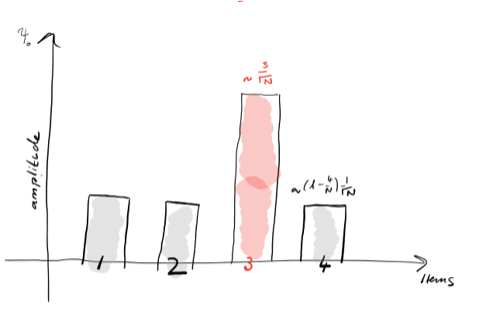
Затем повторяем шаги 2 и 3 до тех пор, пока другие амплитуды не достигнут 0, то есть примерно √N циклов.
Процессы как векторы
Другой (более математически строгий) метод объяснения алгоритма Гровера — это использование векторов.
Шаг 1. Инициализировать вектор |s⟩. Его положение формируется на графике с перпендикулярными осями |w⟩ и |s’⟩ (|s⟩ без |w⟩), что позволяет выразить вектор начального состояния |s⟩ как комбинацию осей |w⟩ и |s’⟩:
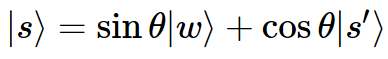
где
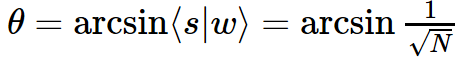
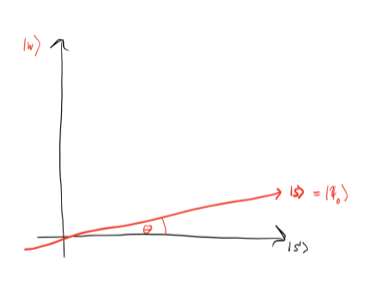
Шаг 2: Применяем отражение оракула U_f к состоянию |s⟩.
На диаграмме вектор |s⟩ (представляющий среднее для всех элементов) опускается. Красный вектор представляет вероятность правильного элемента, отражённого отрицательно. Геометрически оракул является отражением состояния |s⟩ вокруг |s’⟩.
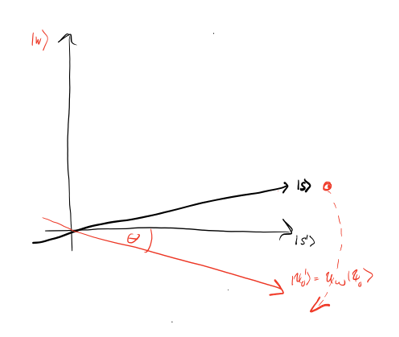
Шаг 3: Применяем отражение U_s к состоянию |s⟩, где U_s=2|s⟩⟨s|−1. Это отображает состояние на U_sU_f|s⟩ и завершает преобразование; поднимает красный вектор ближе к |w⟩, в то же время опуская |s⟩.
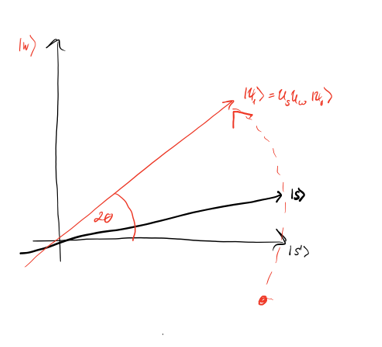
Два отражения всегда соответствуют вращению — преобразование U_sU_f поворачивает начальное состояние |s⟩ ближе к |w⟩.
Поскольку при первом отражении средняя амплитуда снижается, преобразование увеличивает отрицательную амплитуду |w⟩ примерно в 3 раза относительно исходного значения, в то же время уменьшая остальные амплитуды.
Время выполнения
После t шагов мы окажемся в состоянии |ψ.t⟩ = (U.sU.f)^t |s⟩. Вращение нужно применять √N раз, что можно понять, посмотрев на амплитуду состояния |ψ⟩.
Амплитуда |w⟩ растёт линейно с числом приложений — около tN^(—1/2). Тем не менее вероятность попадает в квадратный корень.
Кроме того, если существует несколько решений M, сработают примерно √(N/M) вращений.
Пример с двумя кубитами
Нахождение количества вращений и применение вращения
В случае N = 4 (00, 01, 10, 11) мы можем найти значение теты:

После t шагов применяются вращения:
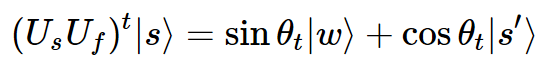
где
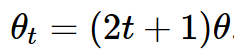
Чтобы найти |w⟩, необходимо найти θ_t=π/2. Со значением теты (θ=π/6) решение уравнения будет t = 1, то есть после t = 1 вращений искомый элемент найден.
Оракулы
Оракулы разные для каждого из N = 4 возможных элементов (|00⟩,|01⟩,|10⟩,|11⟩).
Оракул для |w⟩=|11⟩
Оракул U_f действует на |11⟩ следующим образом. Видно, что состояние |11⟩ перевёрнуто отрицательно.
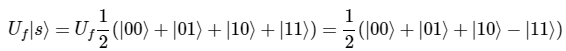
Оракул, способный выполнять эту функцию, является контролируемым квантовым вентилем CZ:
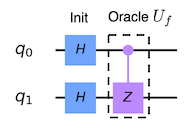
Он переворачивает кубит 11 отрицательно.
Оракул для |w⟩=|00⟩
Оракул U_f действует на |00⟩ следующим образом. Состояние|00⟩ перевёрнуто отрицательно.
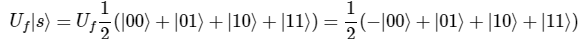
Суммирующая схема:

Оракул для |w⟩=|01⟩ и |w⟩=|10⟩
Оракулы для|w⟩ = |01⟩ (слева) и |w⟩ = |10⟩ (справа)
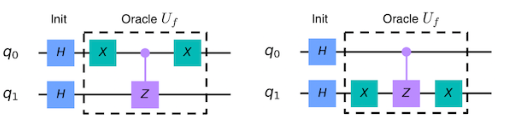
Отражение
Чтобы закончить суммирующую схему, нужно применить дополнительное отражение Us=2|s⟩⟨s|−1, которое ведёт себя так:
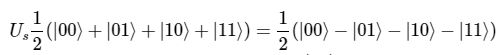
Один из способов записи этого отражения в суммирующей схеме:
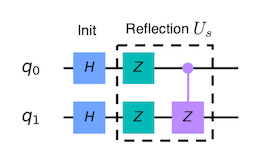
Полная схема для |w⟩ = |00⟩
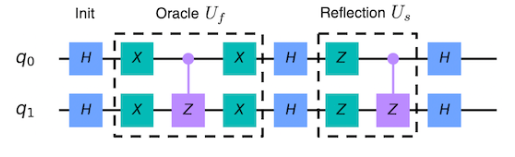
После реализации в симуляторе IBM Qiskit:
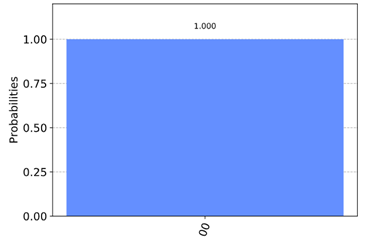
…первый кубит и второй кубит возвращают 0 100% времени.
Применяем суммирующую схему на реальном квантовом компьютере IBM:
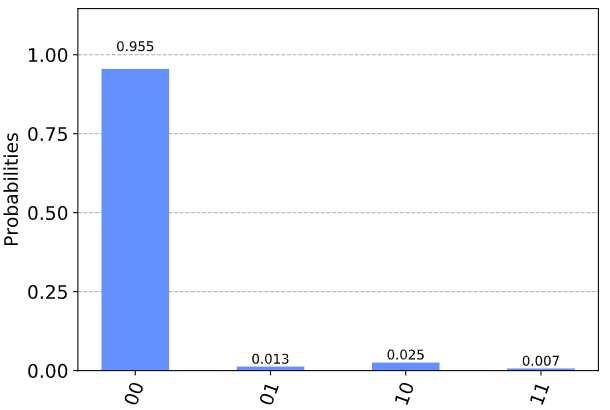
Есть некоторые ошибки из-за ошибок вычислений вентиля, но подавляющее большинство по-прежнему 00.
Алгоритм Гровера можно расширить на несколько кубитов. Для числа кубитов n общее количество элементов, которое сможет поддерживать алгоритм, будет 2 к n.
Надеюсь, вам понравилась эта статья! Чтобы поэкспериметировать, зайдите на IBM Quantum Experience для создания суммирующих схем и реализации квантовых алгоритмов.
Читайте также:
- Значение Data Science в современном мире
- Почему за способностью объяснения модели стоит будущее Data ScienceМой опыт работы с Data Scientist, будучи программным инженером
- Мой опыт работы с Data Scientist, будучи программным инженером
Перевод статьи Andre Ye: Grover’s Algorithm — Quantum Computing






