Введение
В этой статье мы сосредоточимся на том, как деревья бинарного поиска могут быть реализованы на Go и почему они предпочтительнее линейных структур данных, таких как массивы и связанные списки. Пока мы думаем о том, почему деревья имеют преимущество над массивами и списками, рассмотрим основные функциональные возможности, которые мы реализуем в этой статье.
- Вставка узла.
- Обход дерева.
- Получение минимального и максимального элемента.
Что такое дерево?
Дерево — это структура данных, используемая для представления иерархии. Оно обычно состоит из нескольких небольших деревьев. Деревья представляют собой набор узлов, соединенных ребрами. Каждый узел содержит данные определенного типа. Бинарное дерево — это тип дерева, который по определению может иметь максимум два дочерних узла.
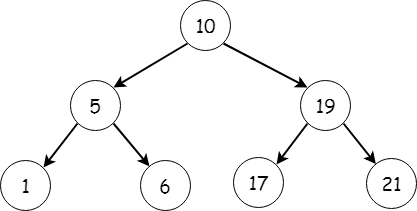
Примечание: бинарное дерево может иметь любой порядок узлов, но двоичное дерево поиска следует определенному порядку, упорядочивая свои узлы, как описано в следующем разделе.
Зачем нужны бинарные деревья?
Представьте себе, что вы находите элемент в массиве. Временная сложность с линейной структурой, такой как массив, — O(n), где n увеличивается по мере увеличения числа элементов для поиска.
Предположим, что данные представлены в виде древовидной структуры. Тогда число шагов, необходимых для нахождения значения, уменьшается более чем наполовину: логарифмическая временная сложность O(logN). Это происходит потому, что всякий раз, когда значение вставляется в двоичное дерево поиска, добавление узла упорядоченно: значение левого дочернего элемента меньше значения родительского, а значение правого узла больше значения родительского узла.
Таким образом, когда мы ищем значение, если оно меньше корня, мы игнорируем всю правую часть дерева и рекурсивно повторяем поиск в левой части дерева.
Терминология
- Узел. Каждый узел содержит указатели на левый и правый дочерний элемент и некоторые данные, связанные с узлом.
- Лист — это узел без потомков.
- Корень — самый верхний узел бинарного дерева.
- Ребро связывает два узла вместе.
Дерево бинарного поиска на Go
Основное внимание в этой статье уделяется реализации бинарного дерева на Golang и нескольких функций для добавления или удаления узлов и т.д. Узел в Go может быть представлен как структура:
TreeNode struct {
val int
left *TreeNode
right *TreeNode
}Эта структура хранит значения int, но она может быть изменена для хранения других типов данных. Левое и правое поля в структуре указывают на другие узлы дерева.
Вставка узла в дерево
Это довольно просто: мы постоянно сравниваем значение вставляемого узла с узлами в двоичном дереве. Если значение вставляемых данных меньше, чем сравниваемый узел, и если левый потомок равен нулю, мы можем вставить новый узел как левый. Иначе мы сравниваем его с левым поддеревом и повторяем процесс.
(t *TreeNode) Insert(value int) error {
if t == nil {
return errors.New("Tree is nil")
}
if t.val == value {
return errors.New("This node value already exists")
}
if t.val > value {
if t.left == nil {
t.left = &TreeNode{val: value}
return nil
}
return t.left.Insert(value)
}
if t.val < value {
if t.right == nil {
t.right = &TreeNode{val: value}
return nil
}
return t.right.Insert(value)
}
return nil
}Каждая из этих функций принимает параметр.
Извлечение минимума
Эта функция рекурсивно находит минимальный элемент дерева:
(t *TreeNode) FindMin() int {
if t.left == nil {
return t.val
}
return t.left.FindMin()
}Мы проверяем значения левых потомков, пока не достигнем nil.
Извлечение максимума
Эта функция находит максимальный элемент дерева. Подход тот же, но до достижения nil обходятся все правые потомки:
(t *TreeNode) FindMax() int {
if t.right == nil {
return t.val
}
return t.right.FindMax()
}Обход бинарного дерева
В правильном дереве бинарного поиска обход всегда будет в порядке возрастания. Обход по порядку — это способ прохождения по двоичному дереву, при котором сначала идет левый дочерний элемент, затем родительский, а после — правый дочерний элемент узла. Код ниже показывает рекурсивный обход.
func (t *TreeNode) PrintInorder() {
if t == nil {
return
}
t.left.PrintInorder()
fmt.Print(t.val)
t.right.PrintInorder()
}Заключение
Двоичные деревья поражают воображение, когда дело доходит до поиска данных, потому что в них он выполняется намного лучше, чем линейный поиск.
Правильное двоичное дерево будет иметь значение левого потомка меньше корня, а значение правого потомка больше корня.
Полный код с большим количеством других функций доступен по адресу https://github.com/puneeth8994/binary-tree-go-impl.
Читайте также:
- Как работает функция Defer в Golang
- Удалённые вызовы процедур в Golang
- Полиморфизм с интерфейсами в Golang
Перевод статьи Puneeth S: Binary Search Trees in Go