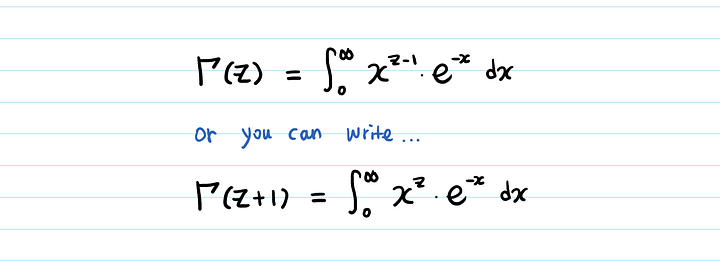Почему это интересно?
Многие распределения вероятностей определяются с использованием гамма-функции, я перечислю лишь некоторые: гамма-распределение, бета-распределение, распределение Дирихле, распределение хи-квадрат, т-распределение Стьюдента и так далее.
Для специалистов по данным или инженеров и исследователей машинного обучения гамма-функция, вероятно, одна из наиболее широко используемых функций, потому что она участвует во множестве распределений. Эти распределения затем используются для генеративных статистических моделей (например, латентного размещения Дирихле), стохастических процессов (таких как модели очередей), байесовском выводе и вариационном выводе. Если вы уже хорошо понимаете гамма-функцию, вы сможете лучше понять множество приложений, в которых она появляется!
1. Зачем нам нужна гамма-функция?
Потому что мы хотим генерализовать факториал!
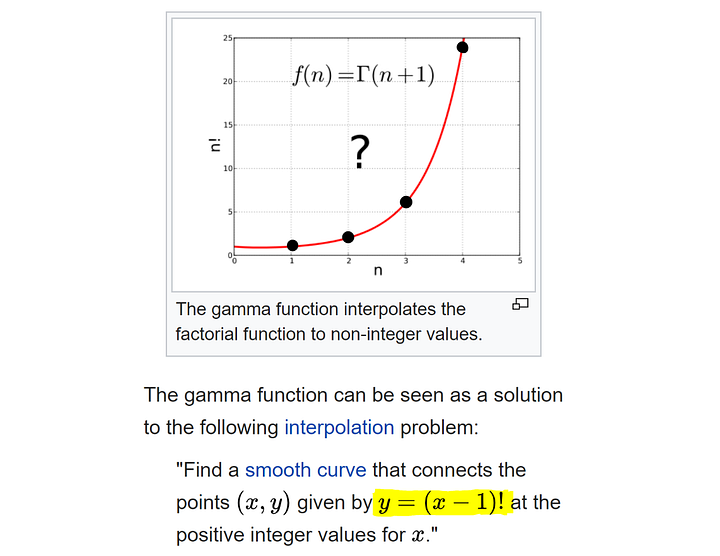
Функция факториала определена только для дискретных точек (для положительных целых чисел — черные точки на графике выше), но мы хотим соединить черные точки. Мы хотим распространить функцию факториала на все комплексные числа. Простую формулу факториала, x! = 1 * 2 * … * x, нельзя использовать непосредственно для дробных значений, потому что она верна только для целых чисел.
Тогда математики стали искать…
“Какие функции плавно соединяют эти точки и предоставляют нам факториалы всех действительных чисел?”

Однако они не могли найти “конечные” комбинации сумм, произведений, степеней, экспонент и логарифмов, которые могли бы выразить x! для действительных чисел, пока…
2. Эйлер в XVIII веке нашел гамма-функцию
Формула выше используется для нахождения значения гамма-функции любого действительного значения z.
Мы хотим вычислить Γ(4.8). Как решить интеграл выше?
Сможете вычислить вручную? Может быть, по частям?
Для меня (и многих других) пока не существует простого и быстрого способа вычислить гамма-функцию дробей вручную (Если вам интересно решить вручную, вот хорошая стартовая точка).
Ладно, забудьте о том, чтобы сделать это аналитически. Вы сможете вычислить этот интеграл от 0 до бесконечности программным способом, добавляя член бесконечное число раз?
Есть несколько способов вычисления. Два из наиболее используемых решений — это формула Стирлинга и приближение Ланцоша.
Для фанатов вычислений: код для гамма-функции (в основном приближение Ланцоша) на более чем 60 языках - C, C++, C#, python, java, etc.
Давайте вычислим Γ(4.8), используя готовый калькулятор.
Мы получим 17.837.
17.837 находится между 3!(= Γ(4) = 6) и 4!(= Γ(5) = 24) — как мы и ожидали.
Когда z — натуральное число, Γ(z) =(z-1)! Скоро мы это докажем.
В отличие от факториала, который принимает только положительные целые числа, мы можем подставлять в z любые действительные или комплексные числа, в том числе и отрицательные. Гамма-функция соединяет черные точки и плавно рисует кривую.
Уточнение: мы интегрируем по x (НЕ по z) от 0 до бесконечности. • x - вспомогательная переменная, которую мы интегрируем. • Мы НЕ подставляем 4.8 в x. Мы подставляем 4.8 в z.
3. Как гамма-функция может интерполировать функцию факториала?
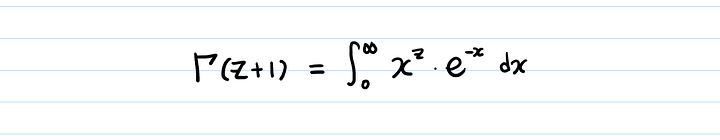
Если вы посмотрите на гамма-функцию, вы заметите две вещи.
Во-первых, это определенно возрастающая функция по отношению к z.
Во-вторых, если z — натуральное число, Γ(z+1) = z!
(Я обещаю, что мы скоро докажем это!)
Значит, можно ожидать, что гамма-функция соединит факториал.
Как гамма-функция получила члены x^z и e^-x?
Я не знаю точно, каким путем шел Эйлер, но именно он открыл натуральное число e, поэтому он, должно быть, много экспериментировал с перемножением e на другие функции, чтобы найти настоящую форму уравнения.
4. Как будет выглядеть график гамма-функции?
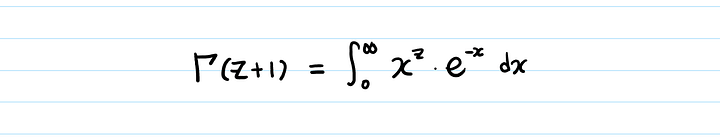
Когда x стремится к бесконечности ∞, первый член (x^z) также стремится к бесконечности ∞, но второй (e^-x) стремится к нулю.
Будет ли гамма-функция сходиться к конечным значениям?
Мы методично покажем, что сходится, используя правило Лопиталя. Но мы также можем увидеть ее сходимость и без особых усилий. Подумаем: мы интегрируем произведение x^z — полиномиальной возрастающей функции — и e^-x —экспоненциально убывающей функции. Так как значение e^-x уменьшается значительно быстрее, чем значение x^z, гамма-функция наверняка сходится и имеет конечные значения.
Давайте построим на каждый график, ведь лучше один раз увидеть, чем сто раз услышать.
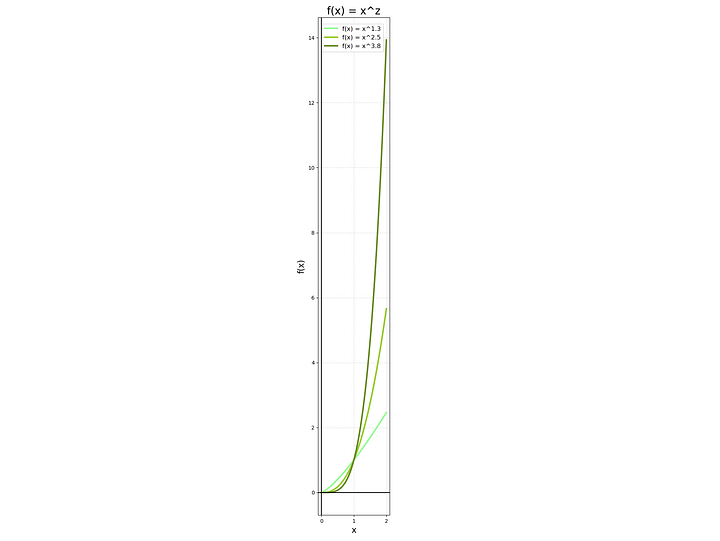
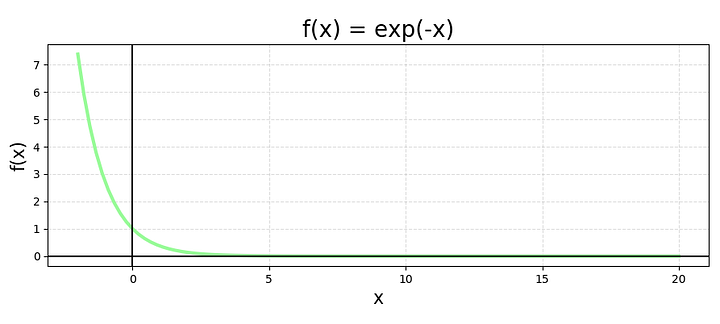
График x^z * e^-x
Давайте рассмотрим случай Γ(4.8).
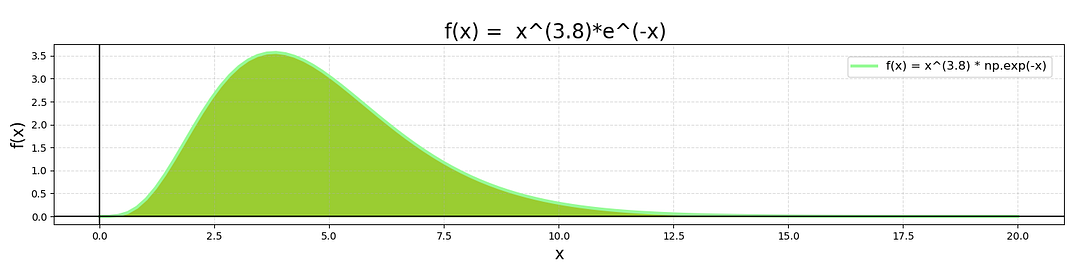
Зеленая область под графиком со значениями от 0 до бесконечности — Γ(4.8) = 3.8!
Для создания красивого графика выше использовался код Python. Постройте такой график сами и увидите, как z меняет форму гамма-функции!
########################
# f(x) = exp(-x) graph #
########################
import matplotlib.pyplot as plt
import numpy as np
# Задаем x и y
x = np.linspace(-2, 20, 100)
y = np.exp(-x)
# Создаем график
fig, ax = plt.subplots()
plt.plot(x, y, label='f(x) = exp(-x)', linewidth=3, color='palegreen')
# Делаем x=0, а y=0 толще
ax.set_aspect('equal')
ax.grid(True, which='both')
ax.axhline(y=0, color='k')
ax.axvline(x=0, color='k')
# Добавляем заголовок
plt.title('f(x) = exp(-x)', fontsize=20)
# Добавляем метки X и y
plt.xlabel('x', fontsize=16)
plt.ylabel('f(x)', fontsize=16)
# Добавляем шкалу
plt.grid(alpha=.4, linestyle='--')
# Показываем график
plt.show()
####################
# f(x) = x^z graph #
####################
import matplotlib.pyplot as plt
import numpy as np
# Задаем x и y
x = np.linspace(0, 2, 100)
y1 = x**1.3
y2 = x**2.5
y3 = x**3.8
# Создаем график
fig, ax = plt.subplots()
plt.plot(x, y1, label='f(x) = x^1.3', linewidth=3, color='palegreen')
plt.plot(x, y2, label='f(x) = x^2.5', linewidth=3, color='yellowgreen')
plt.plot(x, y3, label='f(x) = x^3.8', linewidth=3, color='olivedrab')
# Делаем x=0, y=0 толще
ax.set_aspect('equal')
ax.grid(True, which='both')
ax.axhline(y=0, color='k')
ax.axvline(x=0, color='k')
# Добавляем заголовок
plt.title('f(x) = x^z', fontsize=20)
# Добавляем метки X и y
plt.xlabel('x', fontsize=16)
plt.ylabel('f(x)', fontsize=16)# Add a grid
plt.grid(alpha=.4, linestyle='--')
# Добавляем легенду
plt.legend(bbox_to_anchor=(1, 1), loc='best', borderaxespad=1, fontsize=12)
# Показываем график
plt.show()
###############################
# f(x) = x^(3.8)*e^(-x) graph #
###############################
import matplotlib.pyplot as plt
import numpy as np
# Задаем x и y
x = np.linspace(0, 20, 100)
y = x**3.8 * np.exp(-x)
# Создаем график
fig, ax = plt.subplots()
plt.plot(x, y, label='f(x) = x^(3.8) * np.exp(-x)', linewidth=3, color='palegreen')
ax.fill_between(x, 0, y, color='yellowgreen')
# Делаем x=0, y=0 толще
ax.set_aspect('equal')
ax.grid(True, which='both')
ax.axhline(y=0, color='k')
ax.axvline(x=0, color='k')
# Добавляем заголовок
plt.title('f(x) = x^(3.8)*e^(-x) ', fontsize=20)
# Добавляем метки X и y
plt.xlabel('x', fontsize=16)
plt.ylabel('f(x)' ,fontsize=16)
# Добавляем шкалу
plt.grid(alpha=.4, linestyle='--')
# Добавляем легенду
plt.legend(bbox_to_anchor=(1, 1), loc='upper right', borderaxespad=1, fontsize=12)
# Показываем график
plt.show()5. Свойства гамма-функции
Если усваивать что-то одно из поста, то этот раздел.
Свойство 1.
При z > 1
Γ(z) = (z-1) * Γ(z-1)
или можно записать так
Γ(z+1) = z * Γ(z)Давайте докажем это, используя интегрирование по частям и определение гамма-функции.
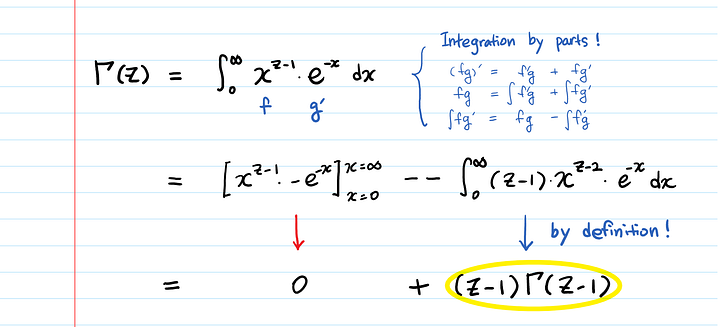
Красивое доказательство!
Свойство 2.
Если n - положительное целое число
Γ(n) = (n-1)!Докажем это, используя свойство 1:
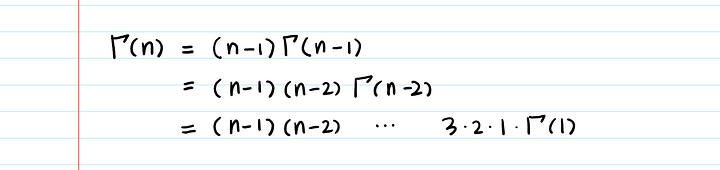
Каково значение Γ(1)?
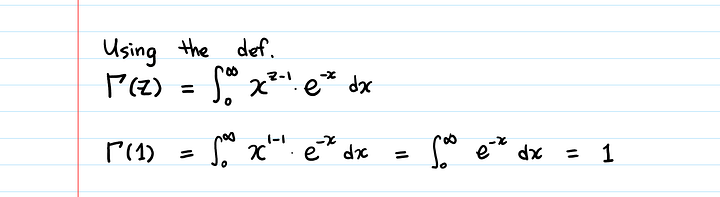
Таким образом, Γ(n) = (n-1)!
Можно также увидеть выражение Γ(n+1) = n! вместо
Γ(n) = (n-1)!.
Просто чтобы сделать правую часть n! вместо (n-1)!
Все, что мы сделали, это уменьшили n на 1.6. Используя свойство гамма-функции, покажем, что плотность вероятности гамма-распределения интегрируется к 1.
Вот доказательство:

Для фанатов доказательств: давайте докажем фрагмент выше, выделенный красным.
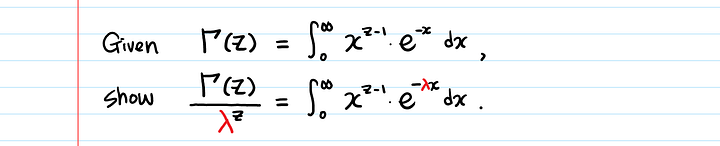
Интегрируем методом подстановки.
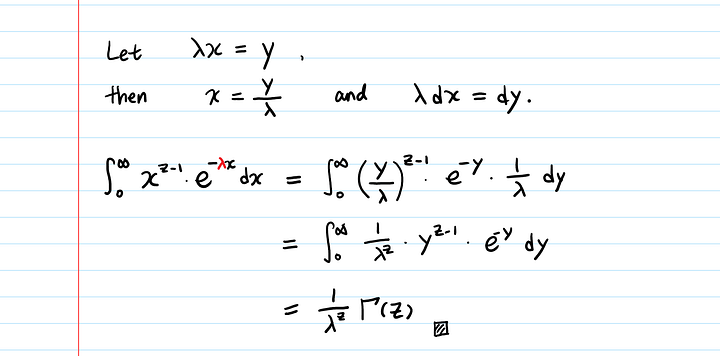
Снова красиво доказано!
Несколько замечаний:
- Возраст гамма-функции.
Она весьма стара, ей около 300 лет (работаете ли вы сейчас над чем-то, что будет использоваться 300 лет спустя? 😉
Интересное примечание: Эйлер ослеп в 64 года, однако больше половины своих работ он написал уже после потери зрения.
2. Несколько интересных значений в точках:
Γ(1/2) = sqrt(?)
Множество интересных способов показать это:
https://math.stackexchange.com/questions/215352/why-is-gamma-left-frac12-right-sqrt-pi
Γ(-1/2) = -2 * sqrt(?)
Γ(-1) = Γ(-2) = Γ(-3) = infinity ∞Сможете доказать?
3. Вот быстрый обзор графиков гамма-функций действительных чисел:
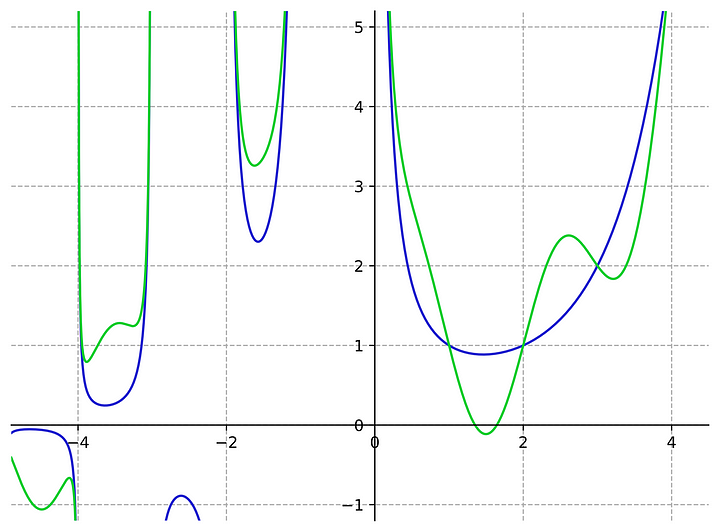
Гамма-функция Γ(z) нарисована синим, Γ(z) + sin(πz) — зеленым. (Заметьте, пересечение в области положительных целых чисел, потому что sin(πz) равен нулю!) Обе являются истинными аналитическими продолжениями факториалов до нецелых чисел.
4. Гамма-функция также появляется в формуле объема n-мерного шара.
Читайте также:
- Значение Data Science в современном мире
- Как составить Data Science портфолио? Часть 1
- Почему за способностью объяснения модели стоит будущее Data Science
Перевод статьи Aerin Kim: Gamma Function — Intuition, Derivation, and Examples