Объясняем производящую функцию моментов

1. Начнем с главного — что такое “момент” в вероятности и статистике?

Скажем, нас интересует случайная переменная X.

Моменты — это ожидаемые значения X, например, E(X), E(X²), E(X³) и т.д.

 Первый момент — E(X),
 Второй момент — E(X²),
 Третий момент — E(X³),
 …
 n-й момент — E(X^n). 

Нам очень хорошо знакомы первые два момента: математическое ожидание μ = E(X) и дисперсия E(X²) − μ². Это важные характеристики X.Математическое ожидание — это среднее значение случайной величины, дисперсия — мера разброса значений. Но должны быть и другие функции, также определяющие распределение. Например, третий момент указывает на асимметрию, четвертый — насколько тяжелы хвосты распределения. 

2. Что же такое производящая функция моментов?

Эта функция определяет распределение значений случайной величины— E(X), E(X²), E(X³), … , E(X^n).

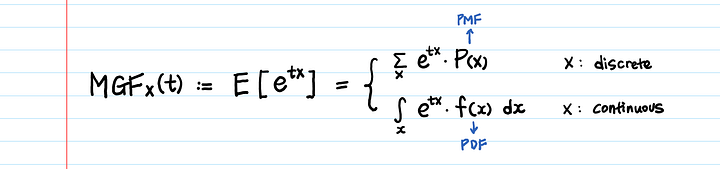
Глядя на определение, вы можете сказать:

“Меня не интересует E(e^tx). Мне нужно E(X^n).”

Возьмите производную от ПФМ n раз и подставьте t = 0. Так вы получите E(X^n).

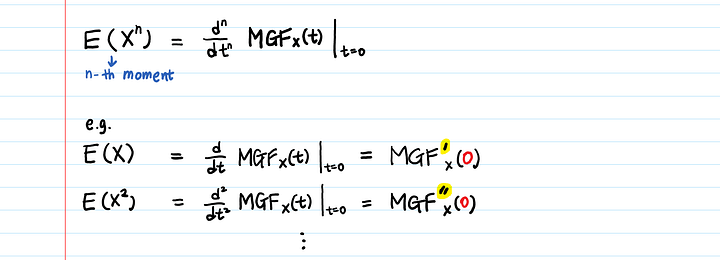
3. Почему n-й момент является n-й производной ПФМ?

Для доказательства используем ряды Тейлора:

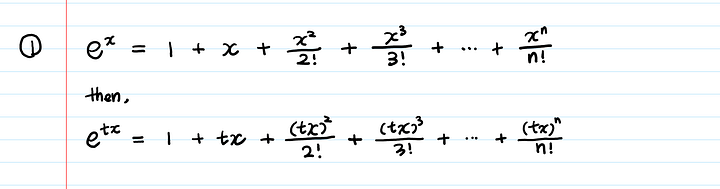
Затем берем ожидаемое значение:

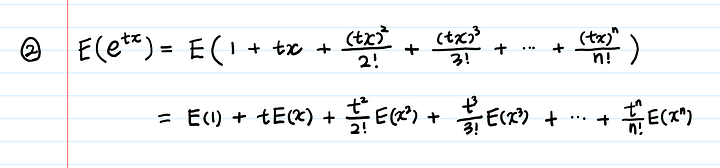
Теперь берем производную по t:

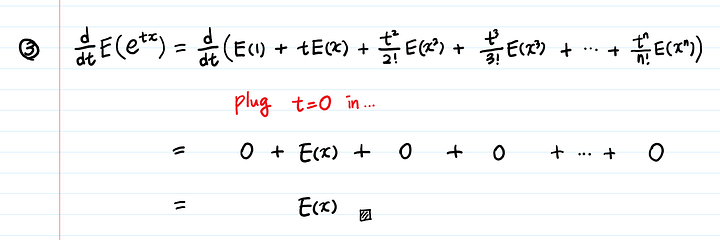
Если возьмем другую производную (то есть производную дважды), получим E(X²).
Снова возьмем производную (третью), получим E(X³), и так далее.

Когда я впервые увидела ПФМ, я не поняла роль t в функции, потому что t показалась произвольной переменной, которая не особенно меня интересовала. Между тем t является вспомогательной переменной — мы вводим t, чтобы использовать исчисление (производные) и обнулить значения (которые нас не интересуют). 

Подождите… но мы можем вычислить моменты, используя определение ожидаемых значений. Зачем нам ПФМ? 

4. Так зачем нам нужна ПФМ? 

Для удобства.

Производящая функция моментов упрощает вычисление моментов.

Как?

В моем учебнике математики написано: “найдите производящую функцию момента биномиального (n, p), пуассонового (λ), экспоненциального (λ), нормального (0, 1) распределений и так далее”. Однако в нем никогда не объяснялось, почему ПФМ полезна и удобна. 

Я думаю, пример ниже порадует вас — самый яркий пример, где есть простое использование ПФМ: ПФМ экспоненциального распределения. (Не знакомы с экспоненциальным распределением? ? Экспоненциальное распределение: восприятие, происхождение, применение)

Начнем с плотности вероятности:

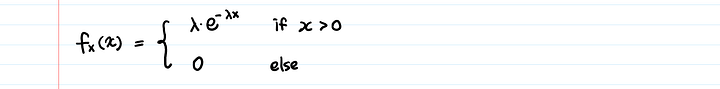
Продифференцируем экспоненциальную ПФМ:

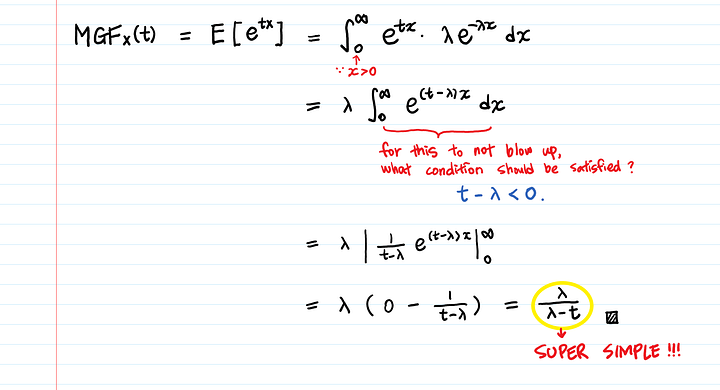
Чтобы ПФМ существовала, должно существовать ожидаемое значение E(e^tx).
Вот почему t — λ < 0 — важное условие: в противном случае интеграл не будет сходиться (это называется тестом на сходимость и проверяется первым делом, когда нужно определить, сходится интеграл или расходится).

Раз у нас есть ПФМ: λ/(λ-t), вычисление моментов становится просто вопросом взятия производных, что проще, чем использование интегралов для расчета ожидаемого значения напрямую.

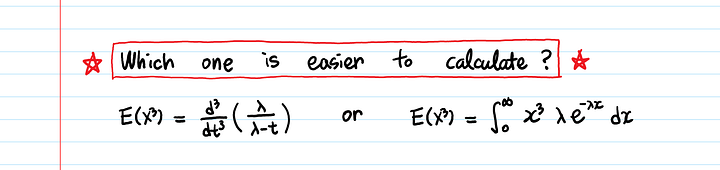
Используя ПФМ, можно находить моменты при помощи производных, а не интегралов! 

Несколько замечаний:

1. Для любой действительной ПФМ M(0) = 1.
   Всякий раз при вычислении ПФМ подставляйте t = 0 и смотрите, получите ли 1.
2. Моменты помогают подробнее описать распределение. Например, можно полностью описать нормальное распределение по первым двум моментам — математическому ожиданию и дисперсии. Чем больше моментов вы знаете, тем больше вы знаете о распределении. Если вы никогда не встречали человека, но знаете его рост, вес, цвет кожи, хобби и т.д., вы по-прежнему не знаете его полностью, но у вас есть много информации о нем.
3. Прелесть ПФМ в том, что, получив ПФМ (когда ожидаемое значение существует), вы можете получить любой n-й момент, так как ПФМ кодирует все моменты случайной переменной в одну функцию, из которой их легко снова извлечь. 
4. Распределение вероятностей однозначно определяется его ПФМ. Если у двух случайных переменных одинаковая ПФМ, они должны иметь одинаковое распределение. 
5. Одно из важнейших свойств распределения — насколько тяжелы его хвосты, особенно, в управлении финансовыми рисками. Если вспомнить финансовый кризис 2008 года, в основе которого по сути лежали неудачные определения вероятностей редких событий, управляющие рисками недооценили эксцесс (“выпуклость”) финансового обеспечения, лежащего в основе торговых позиций фонда. Иногда выглядящие случайными распределения с гипотетически гладкими кривыми риска могут содержать скрытые эксцессы. И мы можем найти их, используя ПФМ!

Читайте также:

• Значение Data Science в современном мире
• Шесть рекомендаций для начинающих специалистов по Data Science
• Почему за способностью объяснения модели стоит будущее Data Science

---

Перевод статьи Aerin Kim: Moment Generating Function Explained