Наука о данных

Биномиальное распределение

09.09.2019

Все знают и любят нормальное распределение. Оно используется в инвестиционном моделировании, A/B-тестах и улучшении производственных процессов (шесть сигм). Но мало кто хорошо знаком с биномиальным распределением. Между тем, результаты бросков монеты следуют биномиальному распределению.

Важно, что здесь работает закон больших чисел. Я также должен сказать, что если мы многократно выполняем один и тот же набор экспериментов (подбрасывая монетку 10 раз) снова и снова, то число решек, наблюдаемых во всех экспериментах, следует биномиальному распределению.

Биномиальное распределение

Дадим более техническое определение. Биномиальное распределение — это распределение вероятностей в последовательности экспериментов, где эксперимент даёт двоичный результат. При этом результаты независимы друг от друга.

Бросок монеты — эксперимент с бинарным результатом. Для ясности уточню: результаты не обязательно должны быть одинаково вероятными, как с бросками симметричной монеты. Условия ниже также соответствуют предварительным требованиям биномиального распределения:

Несимметричная монета.
Опрос случайных людей на улице: “да/нет”.
Попытка убедить посетителей веб-сайта купить продукт (вероятность того, купят они его или нет).

Одна вещь, которая может смутить новичков в теории вероятности и статистике — идея распределения. Мы склонны мыслить детерминистически: «Я подбросил монету 10 раз и получил 6 решек». Результат — 6. Где же распределение?

Распределение происходит из дисперсии. Если мы подбросим 10 монет, то, вероятно, получим разные результаты. Эта дисперсия (неопределенность) создает распределение. Оно сообщает, какие результаты вероятнее, а какие — нет.

Прежде чем писать симуляцию, определимся с переменными.

n: количество экспериментов. У нас 10 бросков — 1 эксперимент.
p: вероятность успеха, 50% для симметричной монеты.
k: желаемое количество удачных попыток. 6 — в нашем примере.

Симуляция на Python

Генерируем случайное число n раз и записываем результаты в списки. Если число равно 0,5 или больше, то считать его решкой, если нет — орлом. И повторим это много раз, в нашем примере 1000.

# Import libraries
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# Входные данные
# Число повторов
trials = 1000
# Бросков в каждом повторе
n = 10
# Вероятность успеха
p = 0.5
# Основная функция
# heads - это список удачных исходов
def run_binom(trials, n, p):
    heads = []
    for i in range(trials):
        tosses = [np.random.random() for i in range(n)]
        heads.append(len([i for i in tosses if i>=0.50]))
    return heads # Выполняем функцию.
heads = run_binom(trials, n, p)# Plot the results as a histogram
fig, ax = plt.subplots(figsize=(14,7))
ax = sns.distplot(heads, bins=11, label='simulation results')ax.set_xlabel("Number of Heads",fontsize=16)
ax.set_ylabel("Frequency",fontsize=16)

Результат выполнения кода на гистограмме:

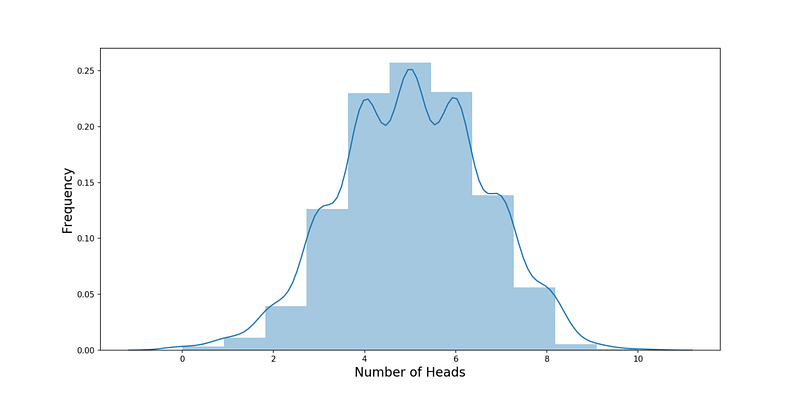
Изменим график так, чтобы он отображал распределение. Используем stats.binom из scipy:

# Plot the actual binomial distribution as a sanity check
from scipy.stats import binom
x = range(0,11)
ax.plot(x, binom.pmf(x, n, p), 'ro', label='actual binomial distribution')
ax.vlines(x, 0, binom.pmf(x, n, p), colors='r', lw=5, alpha=0.5)
plt.legend()
plt.show()

На графике ниже показано моделируемое распределение синим цветом и фактическое — красным. Вывод: биномиальное распределение — достаточно хорошее приближение к реальности. Поэтому вместо того, чтобы тратить время на подбрасывание и записывать результаты, мы можем просто использовать биномиальное распределение!

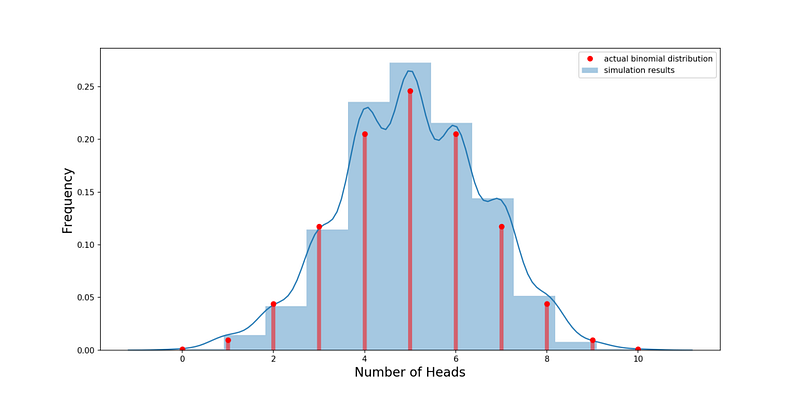
Если мы хотим смоделировать результат последовательности из n экспериментов, то могли бы сделать это, используя биномиально распределенную случайную переменную, например:

np.random.binomial(n, p)

Наконец, ответим на наш вопрос о монетках:

# Вероятность шести решек.
prob_6 = sum([1 for i in np.random.binomial(n, p, size=runs) if i==6])/runs
print('The probability of 6 heads is: ' + str(prob_6))

Это также соответствует первой гистограмме.

Реалистичный пример

Хорошо, а есть что-то кроме монет? Конечно! Представьте себе, что мы аналитики, которым поручено повышение возврата инвестиций в call-центр компании. Сотрудники звонят потенциальным клиентам и продают продукт. Вы посмотрели исторические данные и обнаружили:

В типичном call-центре 50 звонков на 1 сотрудника.
Вероятность конверсии 4%.
Средний доход с конверсии 100$.
В центре 100 сотрудников.
Каждый сотрудник зарабатывает 200$ в день.

Такой код моделирует ситуацию с параметрами n = 50, p = 0.04:

# Количество сотрудников
employees = 100
# Зарплата одного сотрудника
wage = 200
# Звонков на сотрудника
n = 50
# Вероятность успеха
p = 0.04
# Доход с одного звонка
revenue = 100
# Биномиально распределённая переменная
conversions = np.random.binomial(n, p, size=employees)
# Печать ключевых метрик
print('Average Conversions per Employee: ' + str(round(np.mean(conversions), 2)))
print('Standard Deviation of Conversions per Employee: ' + str(round(np.std(conversions), 2)))
print('Total Conversions: ' + str(np.sum(conversions)))
print('Total Revenues: ' + str(np.sum(conversions)*revenue))
print('Total Expense: ' + str(employees*wage))
print('Total Profits: ' + str(np.sum(conversions)*revenue - employees*wage))

Выполнив код, вы увидите что-то вроде этого:

Конверсий на сотрудника: 2,13.
Стандартное отклонение конверсии: 1,48.
Всего конверсий: 213.
Доходы: $21 300.
Расходы: $20 000.
Прибыль: $1 300.

Прибыль в сравнении с расходами невелика. Но посмотрим, как изменяется дневной доход на 1000 симуляций.

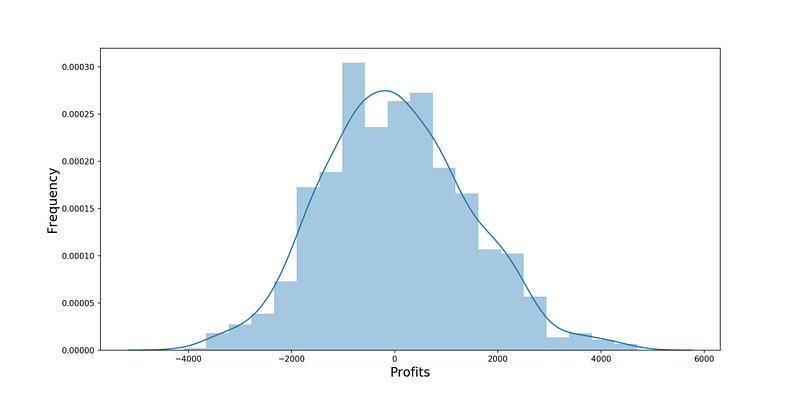
Высока вероятность потерь. Что делать? Результаты каждого сотрудника соответствуют биномиальному распределению, поэтому вот, что можно сделать:

Больше звонить.
Поднять вероятность конверсии.
Увы, снизить зарплаты.

Мы разработали инструмент, формирующий тёплую базу, то есть клиентов, расположенных к покупке. Время разговора сократилось, а конверсия увеличилась. Теперь n = 55, p = 5%. Пересчитаем показатели.

employees = 100
wage = 200 
n = 55
p = 0.05
revenue = 100
# Биномиально распределённая переменная
conversions_up = np.random.binomial(n, p, size=employees)
sims = 1000
sim_conversions_up = 
[np.sum(np.random.binomial(n, p, size=employees)) for i in range(sims)]
sim_profits_up = np.array(sim_conversions_up)*revenue - employees*wage
# Отображаем и сохраняем результат как гистограмму
fig, ax = plt.subplots(figsize=(14,7))
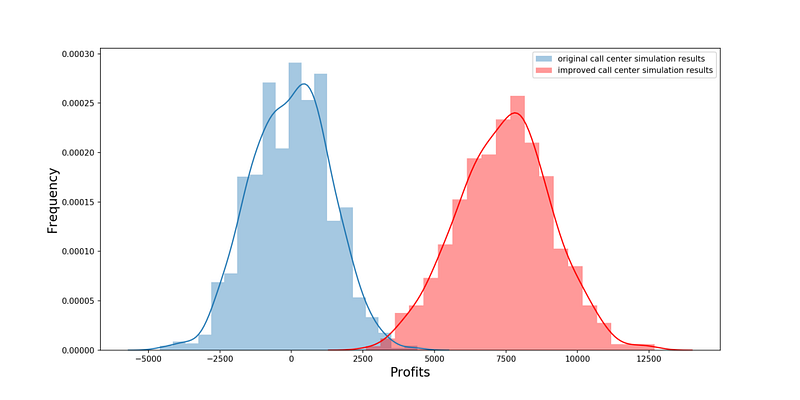
ax = sns.distplot(sim_profits, bins=20, label='original call center simulation results')
ax = sns.distplot(sim_profits_up, bins=20, label='improved call center simulation results', color='red')
ax.set_xlabel("Profits",fontsize=16)
ax.set_ylabel("Frequency",fontsize=16)
plt.legend()

Нам не нужен A/B-тест, чтобы понять, что прибыли будет больше. Красная гистограмма — результат после улучшений.

Итоги

Используя несколько параметров, мы можем прогнозировать результаты для большого количества испытаний.
Однако, крайне важно понимать, в каких ситуациях биномиальное распределение применимо, а в каких — нет.

Проект на Github