Предыдущие части: Часть 1, Часть 2
Логистическая регрессия
Итак, мы уже познакомились с линейной регрессией. Она определяла влияние переменных на другую переменную при условии, что: 1) результирующая переменная непрерывна и 2) отношение между независимыми переменными и результирующей линейное.
Но что, если результирующая переменная категориальная? Тогда и приходит на помощь логистическая регрессия!
Категориальные переменные — те, которые могут принимать лишь значения, обозначающие определённую категорию. Например, дни недели. Если у тебя есть точки на графике, обозначающие события определённого дня, то ни одна точка не может быть между понедельником и вторником. Если что-то произошло в понедельник, то оно произошло в понедельник, всё просто.
Теперь, если мы вспомним, как работает линейная регрессия, то как вообще можно определить линию наилучшего соответствия для чего-то категориального? Это невозможно! Поэтому логистическая регрессия выдаёт не численное значение, а вероятность соответствия той или иной категории. Поэтому модели, использующие логистическую регрессию, чаще всего используются для классификации.
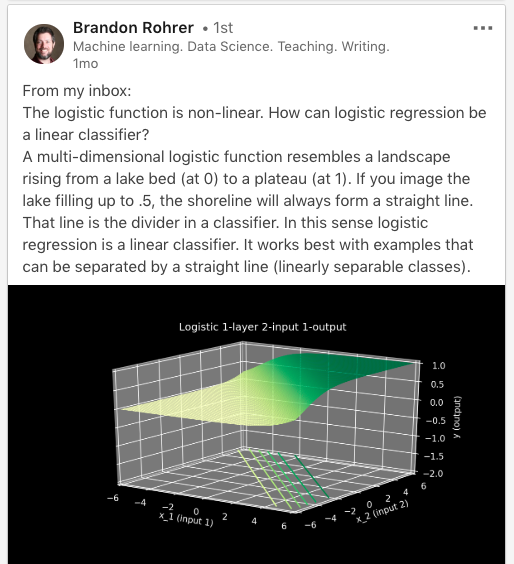
“Из моей почты:
Логистическая функция нелинейна. Как тогда логистическая регрессия может быть линейным классификатором?
Многомерная логистическая функция задаёт поверхность, которая поднимается от озёрной ложи (в точке ноль) к плато (в точке 1). Если вы заполните озеро до значения 0,5, то береговая линия будет прямой. Эта прямая и есть разделительная прямая для классификатора. В этом смысле логистическая регрессия — это линейный классификатор. Она работает лучше всего с линейно разделимыми классами”.
Вернёмся к тому, что мы называем линейную и логистическую регрессию “линейными”. Где же линейная часть логистической регрессии, когда мы не можем определить линию наилучшего соответствия? В мире логистической регрессии результирующая переменная находится в линейных отношениях с логарифмом отношения шансов независимых переменных.
Но что это значит?
Отношение шансов
Ядро логистической регрессии=отношение шансов.
Отношение шансов — это отношение вероятности успешного исхода к вероятности провала. Другими словами, это отношение вероятности того, что событие произойдёт, к вероятности того, что оно не произойдёт.
Для конкретного примера давай рассмотрим школьников, которые пишут тест. Известно, что для девушек отношение шансов того, что они сдадут тест, 5:1, а для парней — 3:10. Это значит, что из 6 девушек 5 скорее всего успешно сдадут тест, а из 13 парней — всего лишь 3. Общее количество учеников равно 19.
То есть отношение шансов и вероятность — одно и то же?
Нет. Вероятность — это отношение количества раз, когда произошло конкретное событие, к количеству всех произошедших событий (например, из 30 подбрасываний монетки в 10 случаях выпала решка).
Отношение шансов — это отношение количества раз, когда произошло конкретное событие, к количеству раз, когда оно не произошло (из 30 подбрасываний в 10 случаях выпала решка, значит, в 20 она не выпала, тогда отношение шансов — 10:20).
Это значит, что вероятность всегда будет в пределах от нуля до единицы, тогда как отношение шансов может расти от нуля до бесконечности. Это проблема для модели логистической регрессии, так как ожидаемые выходные данные должны быть вероятностью, то есть числом в промежутке от нуля до единицы.
Как получить вероятность из отношения шансов?
Давай рассмотрим это на определённой задаче классификации. Например, победит ли твоя любимая футбольная команда в матче с другой командой. Предположим, что отношение шансов того, что твоя любимая команда проиграет — 1:6 или 0,17, а того, что выиграет — 6:1 или 6. Эти числа можно представить на числовой прямой таким образом:
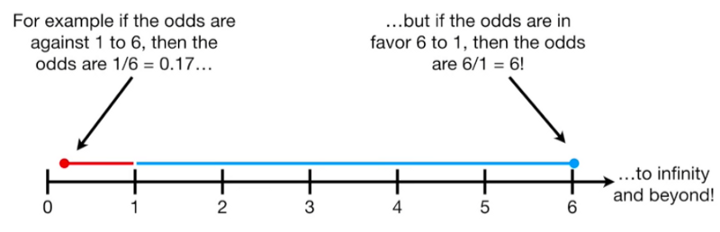
Скорее всего, ты не хочешь, чтобы модель ориентировалась только на модуль отношений шансов. Нужно, чтобы она учитывала, допустим, погоду, игроков и так далее. Для того, чтобы равномерно (симметрично) распределить модуль отношения шансов, мы вычисляем логарифм отношения шансов.
Логарифм отношения шансов
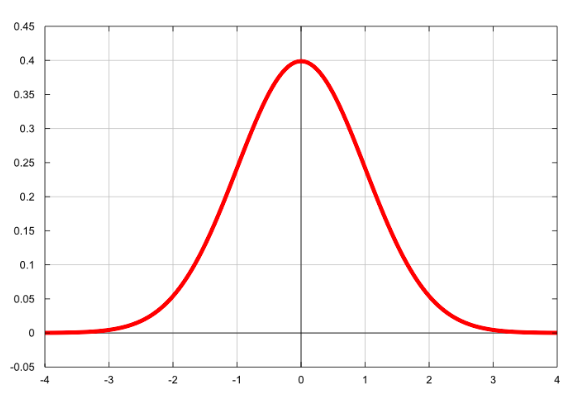
Это натуральный логарифм из отношения шансов. Когда ты берёшь натуральный логарифм от каких-то значений, ты делаешь их более нормально распределёнными. Когда что-то имеет нормальное распределение, с ним очень легко работать.
Когда мы берём натуральный логарифм от отношения шансов, мы распределяем значения от отрицательной бесконечности до положительной. Ты можешь увидеть это на кривой Белла.
Хоть нам и до сих пор нужно число в промежутке от 0 до 1, достигнутая симметрия приближает нас к получению верного результата.
Логит-функция
Это функция, с помощью которой мы получаем логарифм отношения шансов.
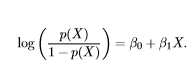
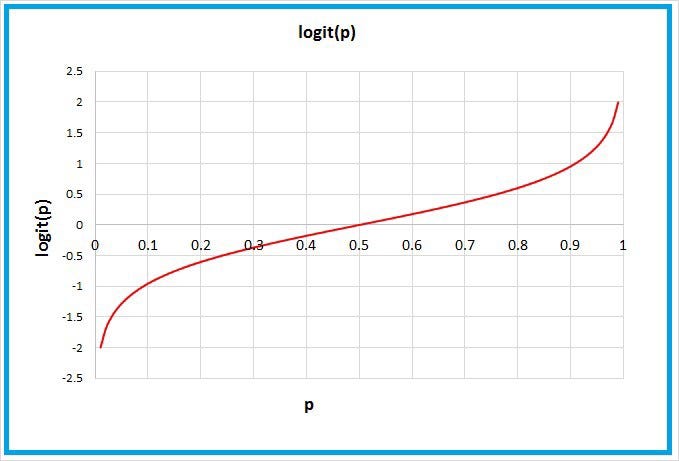
Она просто отображает отношения шансов на промежуток реальных чисел в результате логарифмирования.
Сигмоида
Наша модель до сих пор не выдаёт вероятность, разброс значений слишком большой. Значит, нам нужна сигмоида.
Эта функция, названная в честь s-образной формы её графика, просто выдаёт число, равное обратному отношения шансов. Таким образом, область значений у нас сокращается до [0, 1]. Теперь мы наконец-то можем получить вероятность.
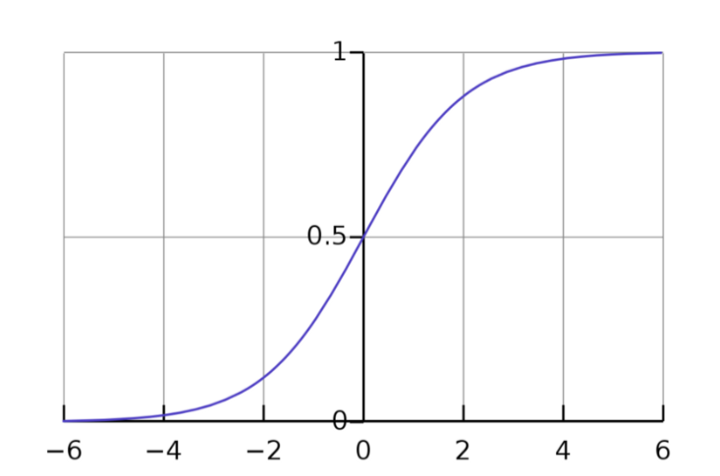
Мы можем взять любой Х на вход и проследить ход работы модели вплоть до предсказанного значения У. Это значение и будет вероятностью отношения Х к тому или иному классу.
Оценка по методу максимального правдоподобия
Мы ещё не закончили.
Ты помнишь, как мы находили линию наилучшего соответствия в линейной регрессии, уменьшая остаточную сумму квадратов (RSS)? Здесь же мы используем оценку по методу максимального правдоподобия (MLE) для более точного предсказания.
MLE позволяет выбрать лучшее предсказание путём вычисления параметров распределения вероятностей, которые наиболее точно описывали бы данные.
Зачем нам вообще нужно определять распределение данных? Во-первых, это круто! Во-вторых, это упрощает работу с данными и делает модель поддающейся обобщению.
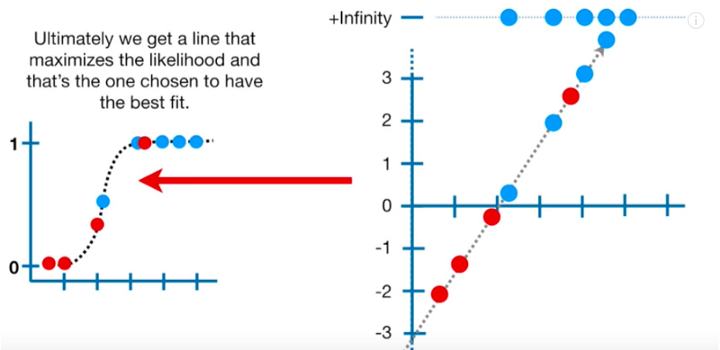
Если говорить в общих чертах, то чтобы использовать MLE для наших данных, мы складываем логарифмы правдоподобной вероятности для точек на s-кривой. Нам нужно найти такую кривую, которая максимизирует логарифмы правдоподобной вероятности для нашего датасета. Для каждой кривой логарифмов отношения шансов мы вновь и вновь вычисляем логарифмы правдоподобной вероятности (как мы вычисляли остаточную сумму квадратов для каждой прямой в линейной регрессии), пока не достигнем максимума.
К слову, мы возвращаемся к вселенной натуральных логарифмов, так как в большинстве случаев работа с логарифмами гораздо удобнее. Так происходит, потому что логарифм — монотонно возрастающая функция, то есть её значение постоянно увеличивается.
Приближения, получаемые в результате процесса MLE — это значения, которые максимизируют так называемую функцию максимального правдоподобия (мы не будем в это углубляться).

И это всё! Теперь моя бабушка и вы знаете о градиентном спуске, линейной и логистической регрессии.
Перевод статьи Audrey Lorberfeld: Machine Learning Algorithms In Layman’s Terms, Part 1 — Часть 3/3






