Предыдущие части: Часть 1
Ридж- и лассо- регрессия
Моя бабушка до сих пор не очень напугана, поэтому продолжаем!
Линейная регрессия не такая уж и пугающая, правда? Это просто метод нахождения связи между чем-то.
Теперь, когда мы знаем, что такое линейная регрессия, можем поговорить о других методах, похожих на неё, например, о ридж-регрессии.
Для понимания линейной регрессии надо было понять метод градиентного спуска. Точно так же для понимания ридж-регрессии необходимо понять, что такое регуляризация.
Специалисты машинного обучения используют методы регуляризации для того, чтобы удостовериться, что модель принимает решение на основании независимых переменных, которые оказывают значительное влияние на результирующую переменную.
Наверное ты думаешь, какая вообще разница, на какие переменные ориентируется наша модель? Ведь если переменные не имеют никакого влияния, то модель линейной регрессии должна их просто проигнорировать. На самом деле всё не так. Мы рассмотрим детали чуть позже, но если говорить вкратце, то мы создаём модель и даём ей кучу данных для обучения. Затем мы тестируем её на тестовых данных. Таким образом, если модель будет учитывать все независимые переменные, то она будет выдавать очень хороший результат на тренировочных данных, но очень плохой на тестовых. Это происходит, потому что модель получается не гибкой и показывает не очень хорошую производительность на данных, которые не содержат каждую, даже малейшую толику того, на чём мы её обучали. Это называется переобучением.
Чтобы понять, что такое переобучение, рассмотрим пример (довольно длинный):
Представим, что недавно ты стала мамой и твой ребёнок очень любит макароны. При этом каждый раз, когда ребёнок ест макароны, окно на кухне приоткрыто, ведь ты любишь прохладу. Затем твой племянник дарит ребёнку комбинезон, и ты начинаешь кормить его макаронами только тогда, когда он одет в этот комбинезон. Вдруг ты решаешь завести собаку, и эта собака исправно сидит рядом с ребёнком в то время, пока он кушает макароны, чтобы ловить то, что упало на пол. Что происходит: ты кормишь ребёнка макаронами, окно на кухне открыто, ребёнок одет в его специальный комбинезон, рядом сидит собака. Так как это твой первый ребёнок, ты думаешь, что он ест макароны только из-за этих трёх окружающих вещей: открытое окно, собака и комбинезон. На этот момент времени твоя модель кормления ребёнка макаронами довольно сложна.
Однажды ты решаешь сходить в гости к бабушке. Тебе нужно покормить ребёнка ужином (конечно же, макаронами). Ты начинаешь паниковать, ведь на кухне нет окна, ты забыла комбинезон дома, и за собакой сейчас присматривают соседи. Тебя настолько выбивает из колеи, что ты вообще забываешь покормить ребёнка и укладываешь его спать голодным.
Вау. Твои действия были неправильными, потому что ты встретилась со сценарием, который не встречала ранее. Однако дома тебе всегда удавалось кормить ребёнка.
После пересмотра модели кормления ребёнка и избавления от “шумов” (вещей, которые, по-твоему, не влияли на любовь ребёнка к макаронам), ты осознаешь единственное, что имеет значение — ты готовишь макароны.
Следующим вечером ты кормишь ребёнка его любимыми макаронами на кухне у бабушки, совсем без окон, в одних только подгузниках и без собаки. И всё проходит хорошо! Теперь твоё понимание того, почему он ест макароны, гораздо проще.
Это то, что делает регуляризация для модели машинного обучения. Она помогает модели обращать внимание лишь на те признаки, которые действительно имеют значение, и избавляться от шумов.
Во всех типах регуляризации присутствует штраф, обозначаемый греческой буквой лямбда: λ. Именно он позволяет сократить количество шумов в данных.
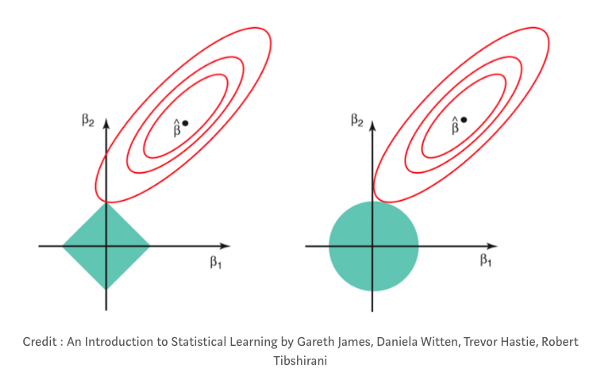
В ридж-регрессии, также называемой L2-регрессией, штраф — это сумма квадратов коэффициентов переменных. Коэффициенты линейной регрессии — просто числа, которые прикреплены к каждой независимой переменной и определяют влияние этой переменной на результирующую переменную. Иногда их называют весами. В ридж-регрессии штрафы уменьшают коэффициенты при соответствующих независимых переменных, но никогда не обнуляют их. Это значит, что шумы всегда будут влиять на результат, но в очень маленькой степени.
Второй тип регуляризации — лассо или L1-регуляризация. Вместо того, чтобы начислять штрафы за каждый признак в данных, штрафы в ней начисляются лишь за признаки с большим значением коэффициентов. К тому же лассо может обнулять значения коэффициентов, тем самым полностью убирая признак из датасета (так как при вычислении результирующей переменной соответствующий признак будет умножен на ноль). Таким образом, с регрессией лассо модель может полностью избавиться от шумов в данных. В некоторых случаях это бывает очень и очень полезно!
Перевод статьи Audrey Lorberfeld: Machine Learning Algorithms In Layman’s Terms, Part 1






