Для нас до сих пор остаётся загадкой то, почему глубокое обучение так хорошо работает. Несмотря на то, что имеется куча догадок, почему глубокие нейронные сети настолько эффективны, никто не уверен в них полностью. Теоретическое понимание глубокого обучения сейчас — область для проведения множества исследований.
В этом уроке мы рассмотрим маленькую часть этой проблемы с необычного ракурса. Мы заставим нейронные сети рисовать абстрактные изображения для нас. Затем проанализируем эти картины для того, чтобы достигнуть большего интуитивного понимания того, что происходит внутри сети. Бонусом, к концу урока вы сможете генерировать картины менее чем за 100 строк кода.
Как было сгенерировано это изображение?
Изображение было сгенерировано при помощи архитектуры под названием CPPN (Compositional Pattern Producing Networks). Мой код имплементирует эту архитектуру при помощи PyTorch.
Один из способов создавать изображения при помощи нейронной сети — вывести целиком всю картину. Например, как в этом случае: нейронная сеть под названием “Генератор” принимает на вход случайные шумы и создаёт всё изображение в выходном слое (размера ширина*высота).
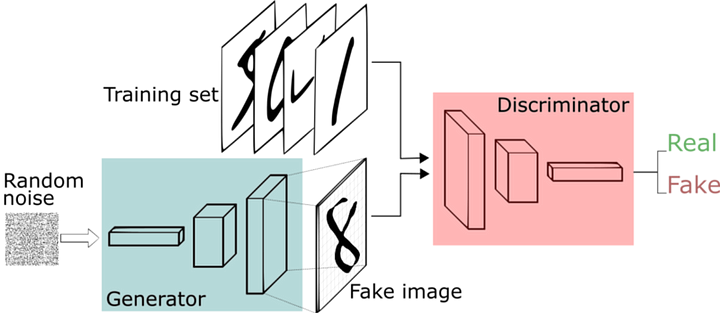
В противоположность этому, CPPN (архитектура, с которой мы будем работать) выводит каждый цвет на заданную позицию, которую принимает на вход.
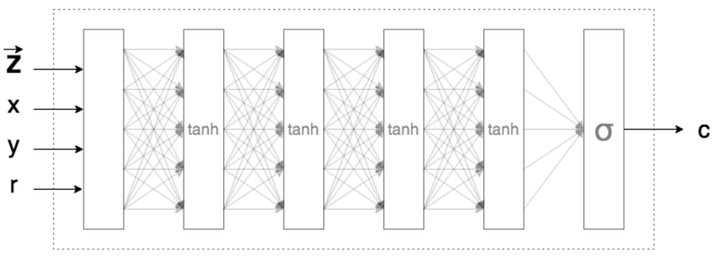
Опустим z и r во входных данных и заметим, что сеть принимает как X и Y значения координат пикселя и выводит его цвет (обозначаемый как c). Так будет выглядеть PyTorch модель для этой сети.
def __init__(self):
super(NN, self).__init__()
self.layers = nn.Sequential(nn.Linear(2, 16, bias=True),
nn.Tanh(),
nn.Linear(16, 16, bias=False),
nn.Tanh(),
nn.Linear(16, 16, bias=False),
nn.Tanh(),
nn.Linear(16, 16, bias=False),
nn.Tanh(),
nn.Linear(16, 16, bias=False),
nn.Tanh(),
nn.Linear(16, 16, bias=False),
nn.Tanh(),
nn.Linear(16, 16, bias=False),
nn.Tanh(),
nn.Linear(16, 16, bias=False),
nn.Tanh(),
nn.Linear(16, 16, bias=False),
nn.Tanh(),
nn.Linear(16, 3, bias=False),
nn.Sigmoid())
def forward(self, x):
return self.layers(x)Заметьте, что функция принимает на вход 2 значения, а возвращает 3 — RGB значения пикселя. Для создания всей картины нужно просто подать все координаты X и Y изображения нужного размера и присваивать пикселю полученное значение цвета.
Эксперименты с нейронной сетью
Когда я впервые попробовал запустить нейронную сеть, я получил вот это изображение.

Я потратил кучу времени, пытаясь понять, почему моя нейронная сеть выдаёт серый цвет вне зависимости от координат пикселя. Этого не должно было происходить. Изменение входных данных должно неизбежно приводить к изменению выходных данных. Также, я знал, что каждый раз, когда нейронная сеть инициализируется заново, вероятнее всего, она создаст совершенно другую картину, так как её параметры задаются случайным образом. Но после нескольких попыток запуска стало понятно, что она всегда выдаёт серый квадрат. Почему?
Сначала подозрение пало на функцию tanh. Возможно, большое количество tanh в последовательных слоях приближало все выходные значения к 0.5 (что соответствует серому цвету). Однако, пост, на котором я основывался, тоже использовал tanh. Всё, что я делал — буквально преобразовывал нейронную сеть с JavaScript в PyTorch без каких-либо изменений.
В конце концов, мне удалось вычислить виновного. Вся проблема в том, как PyTorch инициализирует веса при инициализации самой сети. В PyTorch веса инициализируются случайно от -1/sqrt(N) до 1/sqrt(N), где N — число связей в слое. Тогда, если N=16 для скрытых слоёв, веса будут распределяться от -1/4 до 1/4. Моя гипотеза заключается в том, что такой маленький разброс весов будет давать почти одинаковые значения цвета.
Если все веса в сети были между -1/4 и 1/4, то при умножении на входные данные и сложении, возможно, происходил эффект, определённый центральными предельными теоремами.
Центральные предельные теоремы — класс теорем в теории вероятностей, утверждающих, что сумма достаточно большого количества слабо зависимых случайных величин, имеющих примерно одинаковые масштабы (ни одно из слагаемых не доминирует, не вносит в сумму определяющего вклада), имеет распределение, близкое к нормальному.
Вспомним, как вычислялось значение на результирующих слоях.
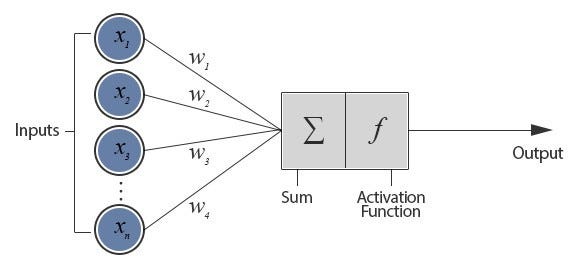
В нашем случае, первый входной слой получал 2 значения: X и Y. В следующем скрытом слое 16 нейронов. То есть, каждый нейрон второго слоя получает 2 значения, умноженных на веса от -1/4 до 1/4. Они суммируются и передаются активирующей функции tanh, становясь новыми значениями для отправления третьему слою.
Теперь, от второго слоя, каждому из 16 нейронов третьего слоя посылается 16 входных значений. Обозначим каждое из этих значений буквой z. Тогда значение, передаваемое каждому нейрону третьего слоя будет таким:
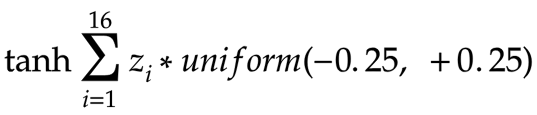
Выдвинем ещё одно предположение. Из-за того, что разброс весов мал, значения z (которые являются входными X и Y, умноженными на веса и переданными через функцию tanh) тоже будут мало отличаться. Тогда формулу можно переписать в таком виде:
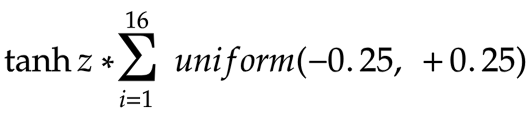
И, скорее всего, сумма 16 весов от -0.25 до 0.25 для каждого нейрона будет стремиться к нулю. Даже если на первом слое сумма не была близка к нулю, 8 слоёв нейронной сети делают вероятность получения нулевой суммы достаточно высокой. Следовательно, вне зависимости от входных значений X и Y, сумма значений, передаваемых нейронам последующих слоёв (сумма весов * входные данные), будет стремиться к нулю. Tanh будет приравнивать их к нулю, поэтому во всех последующих слоях эти значения остаются нулевыми.
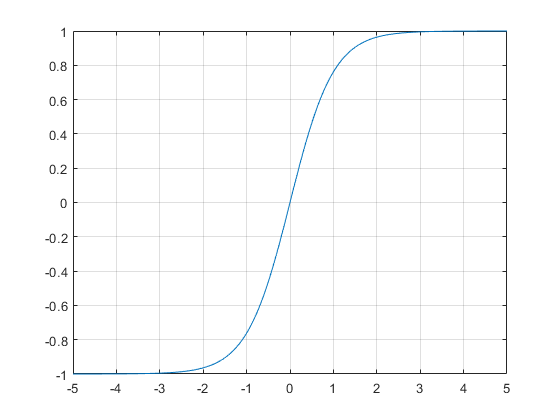
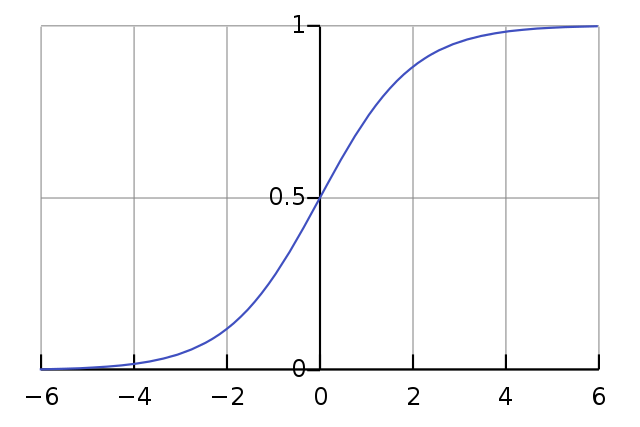
Что же является причиной получения серого цвета? Sigmoid (функция последнего слоя) всегда получает 0 в качестве входного значения, которое сопоставляется 0.5 (0.5 — серый, 0 — чёрный, 1 — белый).
Как исправить серый квадрат?
Как мы определили, виновником оказался маленький разброс весов. Следующим логичным шагом будет увеличить его. Я изменил инициализацию, задав разброс весов от -100 до 100. Запуск нейронной сети дал мне вот такой результат:

Прогресс очевиден, значит, моя гипотеза оказалась верной.
Однако, сгенерированное изображение слишком простое.
Наша нейронная сеть умножает входные значения на веса, отправляет их функции tanh и выводит цвет при помощи функции sigmoid. Мне уже удалось решить проблему с весами, могу ли я что-то изменить, чтобы сделать выходное изображение более интересным?
Заметим, что изображение выше было сгенерировано функцией, принимающей на вход данные X,Y — координаты пикселя от 0,0 до 128х128 (так как размер картинки — 128 на 128). Это значит, что моя сеть не получала на вход, например, отрицательные значения. Также, tanh получала на вход либо очень большие, либо очень маленькие значения, которые приводились к 1 или к -1. Поэтому в качестве выходных значений пикселей чаще всего получались базовые цвета. Например, полученный голубой в RGB будет представляться как (0, 1, 1).
Как сделать изображения интереснее?
Как и в оригинальном посте, на который я ориентировался, я решил нормализовать X и Y. Теперь, вместо того, чтобы подавать на вход X, я подавал (X/размер_изображения)-0.5. Тогда, вне зависимости от размера изображения, мои X и Y всегда оставались ограниченными -0.5 и 0.5. Таким способом я получил вот это изображение:
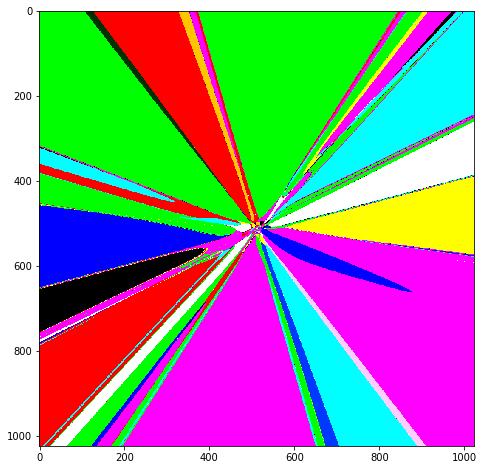
Интересно, что на предыдущем изображении линии увеличивались к нижнему правому углу, потому что значения X и Y увеличивались. Здесь, благодаря тому, что значения нормализованы, секторы цветов расширяются к краям изображения.
Тем не менее, картина всё ещё далека от той, которую хотелось бы увидеть.
Как сделать изображение ещё более интересным?
Если приглядеться, можно заметить, что центр картины отличается от краёв — он выглядит гораздо интереснее. Это подсказка от богов математики: нам нужно приблизить центр для получения чего-то большего.
Есть три способа это сделать:
- Создать изображение больше. Координаты пикселей нормализуются, поэтому мы просто можем запустить нейронную сеть для изображения с большим разрешением и вырезать центр полученной картины.
- Умножить значения X и Y на небольшое число (зум-фактор), что сделает почти то же самое, что и предыдущий способ, за исключением того, что нам не нужно будет обрезать результирующее изображение
- Так как выходная картинка определяется входными данными, умноженными на вектор весов, вместо того, чтобы уменьшать входные данные, мы можем уменьшить значения весов от (-100, 100) до, например, (-3, 3). Однако, помните о том, что происходило, когда веса варьировались от -0.25 до 0.25.
Вот что получилось, когда я решил использовать второй способ и умножил значения входных данных на 0.01:

А вот что вышло, когда я решил применить третий метод и инициализировал весы в промежутке (-3, 3):

Больше экспериментов
Я изменил инициализацию весов на нормальное распределение (среднее значение между 0 и стандартным отклонением от 1) и сгенерировал несколько изображений.



Затем я убрал все скрытые слои:

Затем оставил 1 скрытый слой вместо 8 по умолчанию:

И, наконец, результат 16 скрытых слоёв:

Как вы видите, изображение становится всё более сложным с увеличением количества скрытых слоёв. Мне стало интересно, что получится, если вместо удвоения количества слоёв я увеличу количество нейронов в слоях (с 16 до 32). Вот что получилось:

Заметим, что несмотря на то, что количество весов не меняется, сеть с удвоенным количеством слоёв выдаёт картинку меньшего разрешения по сравнению с той, что выдаёт сеть с удвоенным количеством нейронов. Пиксели говорят о том, что в этих регионах функция резко меняет своё значение и при увеличении это будет заметно ещё больше. В это же время, сеть с удвоенным количеством нейронов выдаёт более гладкую функцию.
Всё это, несомненно, говорит о том, что глубина делает нейронные сети более сложными.
Сложность вычисляемой функции экспоненциально растёт с ростом глубины.
Это в точности то, что мы видим. Универсальная теорема аппроксимации (теорема Цыбенко) утверждает, что в теории нейронная сеть с одним скрытым слоем может аппроксимировать любую непрерывную функцию многих переменных с любой точностью. Но, на практике, чем глубже сеть, тем более сложное отображение из входных данных в выходные она может представить.
Интересные эксперименты без особого смысла
Что произойдёт, если увеличить количество нейронов каждого слоя с 8 до 128?

Что, если мы начнём со 128 нейронов на каждый скрытый слой, но каждый последующий слой мы будем уменьшать их количество?
self.layers = nn.Sequential(nn.Linear(2, hidden_n, bias=True),
nn.Tanh(),
nn.Linear(128, 64, bias=False),
nn.Tanh(),
nn.Linear(64, 32, bias=False),
nn.Tanh(),
nn.Linear(32, 16, bias=False),
nn.Tanh(),
nn.Linear(16, 8, bias=False),
nn.Tanh(),
nn.Linear(8, 4, bias=False),
nn.Tanh(),
nn.Linear(4, 3, bias=False),
nn.Sigmoid())Вот что вышло:

Есть ещё куча экспериментов, которую можно проделать для получения интересных картинок, поэтому я оставлю ссылку на код, с которым можно их проделать. Попробуйте другую архитектуру, способ активации, параметры слоя. Если у вас получится что-то интересное, пишите и я поделюсь вашим результатом.
Или, можно объединить изображения, созданные нейронной сетью и философские цитаты, сгенерированные при её же помощи.

Перевод статьи Paras Chopra: Making deep neural networks paint to understand how they work






