Python: подробное руководство по Statsmodels

Изучим Statsmodels на практических примерах статистического моделирования, тестирования гипотез и анализа данных.

В науке о данных и аналитике статистическое моделирование  —  это основа для понимания закономерностей данных, формирования прогнозов, принятия обоснованных решений. Статистические модели создаются и интерпретируются в научных исследованиях, бизнес-прогнозах, моделях машинного обучения.

В Python, популярнейшем языке науки о данных, много библиотек для анализа данных. Среди них выделяется statsmodels  —  мощный инструмент статистического моделирования и проверки гипотез. В отличие от других библиотек, statsmodels ориентирована на всесторонний статистический анализ, а не ML-алгоритмы. Поэтому является обязательным инструментом дата-сайентистов.

Начнем с установки и настройки библиотеки, изучим ее структуру и расширенный функционал: от простого разведочного анализа данных до продвинутых методов статистического анализа для построения надежных прогностических моделей.

Библиотека statsmodels

Прежде чем переходить к функционалу statsmodels, настроим среду и разберем базовую структуру этой библиотеки.

Установка и настройка

Устанавливаем statsmodels так:

pip install statsmodels

Или с Anaconda:

conda install -c conda-forge statsmodels

Теперь импортируем библиотеку в Python-скрипте или Jupyter Notebook:

import statsmodels.api as sm
import statsmodels.formula.api as smf

Структура statsmodels

Библиотека организована по подмодулям статистического моделирования:

• api: основная точка входа для функционала statsmodels.
• formula.api: фреймворк формул, аналогичный интерфейсу формул языка R.
• regression: классы и функции для моделирования линейной регрессии.
• tsa: расшифровывается как time series analysis, то есть анализ временны́х рядов, здесь содержатся модели для анализа и прогнозирования данных временно́го ряда.
• genmod: обобщенные линейные  —  и не только линейные  —  модели.
• graphics: инструменты для графического представления статистических данных.

Вот пример использования statsmodels:

import statsmodels.api as sm
import numpy as np

# Генерирование синтетических данных
np.random.seed(0)
X = np.random.rand(100, 1)
X = sm.add_constant(X)  # Предиктору добавляется свободный член
y = 3 + 2 * X[:, 1] + np.random.randn(100)

# Подгонка линейной регрессионной модели
model = sm.OLS(y, X)
results = model.fit()

# Сводка результатов регрессии
print(results.summary())

В этом примере генерируются синтетические данные, осуществляется подгонка простой линейной регрессионной модели со statsmodels, выводится сводка результатов регрессии. Функцией sm.add_constant(X) в матрицу предикторов добавляется свободный член, что важно для подгонки свободного коэффициента регрессионной модели.

Разведочный анализ данных со statsmodels

Функциями statsmodels выполняется разведочный анализ данных: вычисление количественных показателей распределения, генерирование визуализаций, получение представления о структуре данных.

Рассмотрим эту функциональность.

Разведочный анализ данных  —  важнейший этап в процессе анализа данных. Здесь обобщаются основные характеристики данных, обычно визуальными методами. Разведочный анализ данных упрощается в statsmodels функциями для вычисления количественных показателей распределения и генерирования визуализаций.

Импорт данных и предварительное исследование

Сначала импортируем набор данных Iris, хотя для statsmodels сгодятся фреймы данных Pandas, массивы NumPy и другие структуры данных:

import statsmodels.api as sm
import pandas as pd

# Загрузка набора данных Iris из «statsmodels»
iris = sm.datasets.get_rdataset("iris").data

# Отображение первых строк набора данных
print(iris.head())

Этим фрагментом кода загружается набор данных Iris и выводятся начальные строки, создается первое представление о данных.

Вывод:

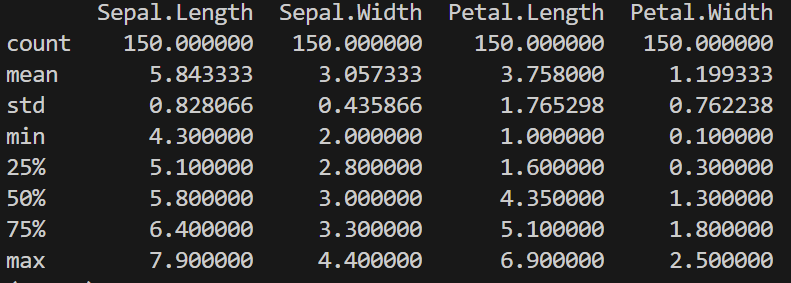
Количественные показатели распределения

Количественные показатели распределения  —  это сводка данных, в том числе параметры, характеризующие положение центра, вариацию и форму распределения данных. Со statsmodels такие показатели вычисляются легко:

# Количественные показатели распределения с pandas
print(iris.describe())

Здесь выводятся среднее арифметическое, стандартное отклонение, минимальное и максимальное значения, а также квартили для каждого числового столбца в наборе данных.

Вывод:

Визуализации

С визуализациями проще понять распределение данных и выявить закономерности или аномалии. statsmodels интегрируется с другими библиотеками визуализации Python, такими как Matplotlib и Seaborn. Вот примеры создаваемых визуализаций:

Гистограмма

import matplotlib.pyplot as plt

# Гистограмма длины чашелистиков
plt.hist(iris['Sepal.Length'], bins=20, edgecolor='black')
plt.title('Histogram of Sepal Length')
plt.xlabel('Sepal Length')
plt.ylabel('Frequency')
plt.show()

Вывод:

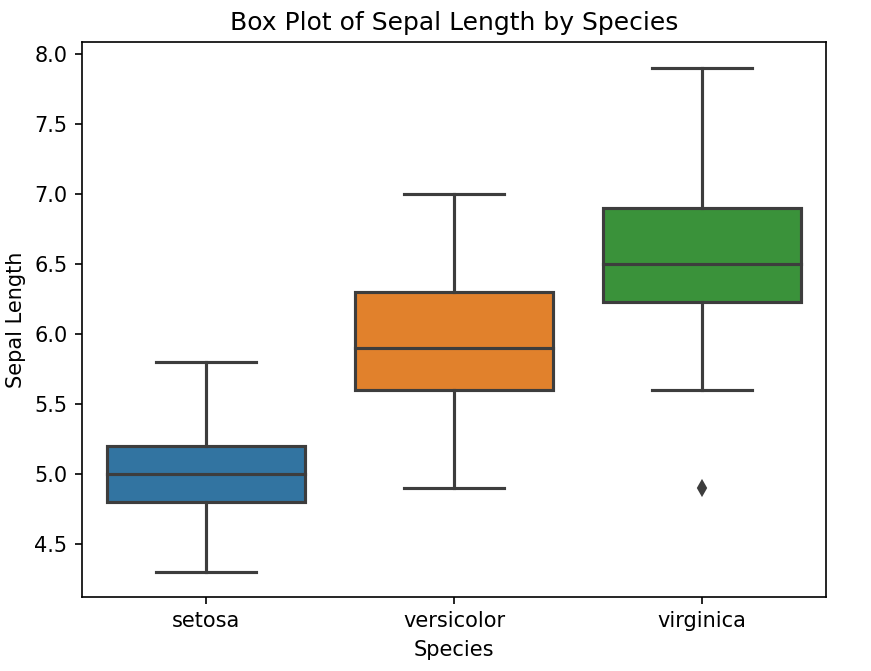
Диаграмма «ящик с усами»

import seaborn as sns

# Диаграмма «ящик с усами» длины чашелистиков по видам
sns.boxplot(x='Species', y='Sepal.Length', data=iris)
plt.title('Box Plot of Sepal Length by Species')
plt.xlabel('Species')
plt.ylabel('Sepal Length')
plt.show()

Вывод:

Точечная диаграмма

# Точечная диаграмма длины и ширины чашелистиков
sns.scatterplot(x='Sepal.Length', y='Sepal.Width', hue='Species', data=iris)
plt.title('Scatter Plot of Sepal Length vs. Sepal Width')
plt.xlabel('Sepal Length')
plt.ylabel('Sepal Width')
plt.show()

Вывод:

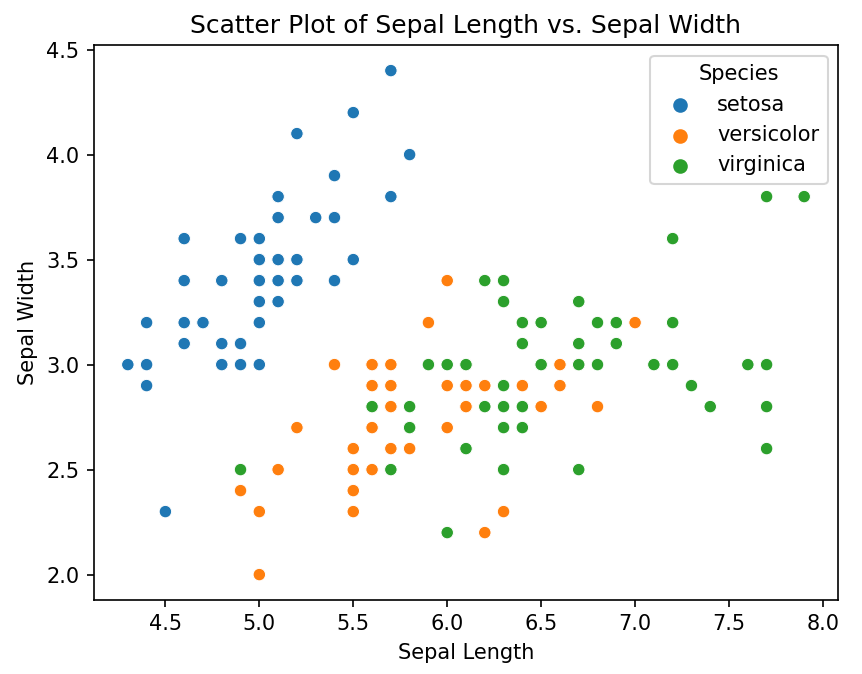
Этими визуализациями формируется полное представление о распределении данных и отношениях между переменными.

Теперь изучим основной функционал по статистическим моделям statsmodels.

Статистические модели в statsmodels

Главное преимущество statsmodels  —  статистические модели для выполнения анализа данных: от простой линейной регрессии до сложного анализа временны́х рядов. Изучим ключевые статистические модели statsmodels.

Линейная регрессия

Линейная регрессия  —  одна из простейших и популярнейших статистических моделей. Ею моделируется отношение между зависимой переменной и одной или несколькими независимыми переменными путем подгонки линейного уравнения к наблюдаемым данным.

Пример простой линейной регрессии:

import statsmodels.api as sm
import numpy as np

# Генерирование синтетических данных
np.random.seed(0)
X = np.random.rand(100, 1)
X = sm.add_constant(X)  # Предиктору добавляется свободный член
y = 3 + 2 * X[:, 1] + np.random.randn(100)

# Подгонка линейной регрессионной модели
model = sm.OLS(y, X)
results = model.fit()

# Сводка результатов регрессии
print(results.summary())

Для простой линейной регрессии в этом примере создаются синтетические данные, при помощи sm.OLS подгоняется модель, выводится сводка результатов регрессии.

Вывод:

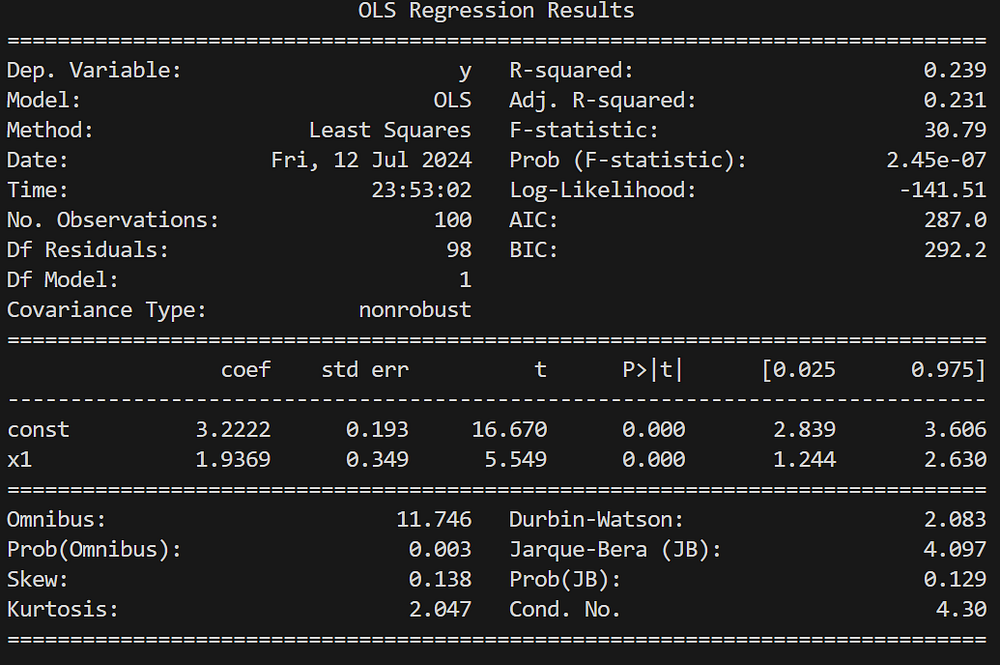
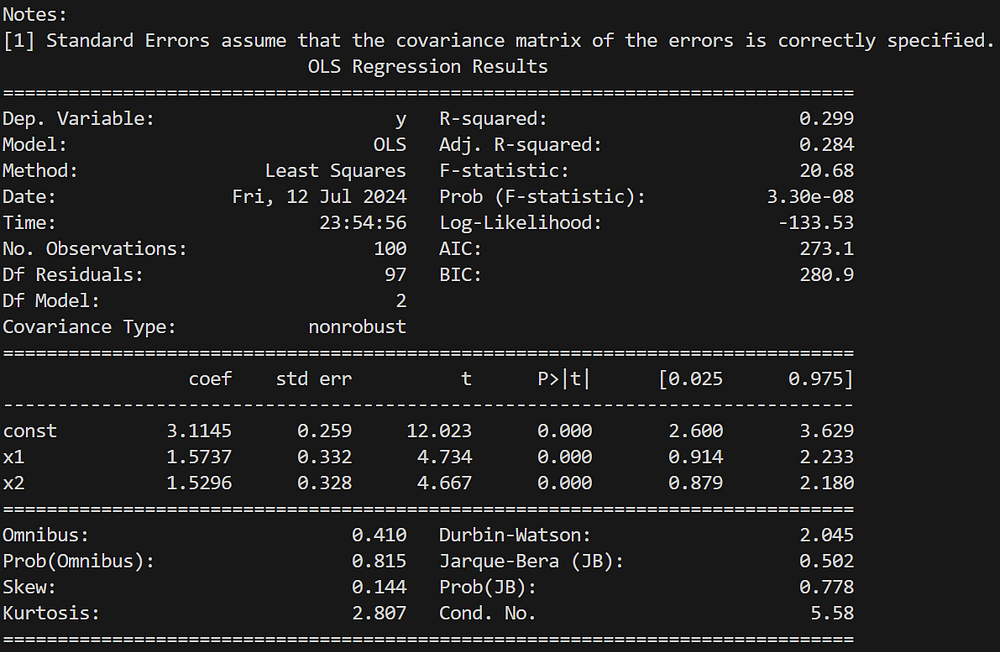
Пример множественной линейной регрессии:

# Для множественной регрессии генерируются синтетические данные
np.random.seed(0)
X = np.random.rand(100, 2)
X = sm.add_constant(X)
y = 3 + 2 * X[:, 1] + 1.5 * X[:, 2] + np.random.randn(100)

# Подгонка модели множественной линейной регрессии
model = sm.OLS(y, X)
results = model.fit()

# Сводка результатов регрессии
print(results.summary())

Здесь предыдущий пример расширяется предикторами регрессионной модели.

Вывод:

Логистическая регрессия

Логистическая регрессия используется, когда зависимая переменная  —  бинарная. Ею моделируется вероятность класса по умолчанию  —  обычно это 1  —  как функции предикторных переменных.

Пример логистической регрессии:

import statsmodels.api as sm
import pandas as pd
from sklearn.datasets import load_iris

# Загрузка набора данных Iris
iris = load_iris()
df = pd.DataFrame(data=iris.data, columns=iris.feature_names)
df['target'] = iris.target

# Использование только двух классов для бинарной классификации
df = df[df['target'] != 2]

# Добавление свободного члена
df['intercept'] = 1.0

# Определение независимой и зависимой переменных
X = df[['sepal length (cm)', 'sepal width (cm)', 'intercept']]
y = df['target']

# Подгонка модели логистической регрессии
logit_model = sm.Logit(y, X)
result = logit_model.fit()

# Сводка результатов логистической регрессии
print(result.summary())

В этом примере набор данных Iris загружается и фильтруется для включения только двух классов, при помощи sm.Logit подгоняется модель логистической регрессии.

Анализ временны́х рядов

Анализ временны́х рядов  —  это анализ точек данных, собранных или записанных с определенной периодичностью. В statsmodels он поддерживается авторегрессией, скользящим средним, ARIMA-моделями.

Пример ARIMA-модели:

import statsmodels.api as sm

# Загрузка набора данных для временны́х рядов
data = sm.datasets.co2.load_pandas().data

# Обработка пропусков значений заполнением вперед
data = data.fillna(method='ffill')

# Подгонка ARIMA-модели
arima_model = sm.tsa.ARIMA(data['co2'], order=(1, 1, 1))
arima_result = arima_model.fit()

# Сводка результатов ARIMA-модели
print(arima_result.summary())

# Построение графика прогноза
forecast = arima_result.forecast(steps=12)
plt.plot(data.index, data['co2'], label='Observed')
plt.plot(forecast.index, forecast, label='Forecast', color='red')
plt.title('ARIMA Model Forecast')
plt.xlabel('Date')
plt.ylabel('CO2 Levels')
plt.legend()
plt.show()

В этом примере загружается набор данных для временны́х рядов уровней CO₂, обрабатываются пропуски значений, подгоняется ARIMA-модель, строится график прогнозных значений.

Обобщенные линейные модели

В обобщенных линейных моделях линейные модели дополняются переменными реакции, модели распределения ошибок которых отличаются от нормального распределения. К обобщенным линейным моделям относятся логистическая регрессия, регрессия Пуассона и т. д.

Пример регрессии Пуассона:

import statsmodels.api as sm
import pandas as pd

# Генерирование синтетических данных
data = pd.DataFrame({
    'hours_studied': np.random.poisson(5, 100),
    'exam_passed': np.random.binomial(1, 0.5, 100)
})

# Добавление свободного члена
data['intercept'] = 1.0

# Определение независимой и зависимой переменных
X = data[['hours_studied', 'intercept']]
y = data['exam_passed']

# Подгонка модели регрессии Пуассона
poisson_model = sm.GLM(y, X, family=sm.families.Poisson())
poisson_result = poisson_model.fit()

# Сводка результатов регрессии Пуассона
print(poisson_result.summary())

В этом примере генерируются синтетические данные, определяются независимая и зависимая переменные, при помощи sm.GLM подгоняется модель регрессии Пуассона.

Продвинутый функционал statsmodels

Возможности статистического анализа расширяются продвинутым функционалом statsmodels: проверкой гипотез, диагностикой моделей, формульным API. Рассмотрим подробнее.

Проверка гипотез

Это фундаментальная основа статистического анализа, связанная с получением выводов о статистических совокупностях на основе образца данных. В statsmodels имеются разнообразные статистические тесты.

Пример t-критерия Стьюдента

T-критерием Стьюдента определяется значимость различий средних значений двух групп.

from statsmodels.stats.weightstats import ttest_ind

# Генерирование синтетических данных для двух групп
np.random.seed(0)
group1 = np.random.normal(5, 2, 100)
group2 = np.random.normal(5.5, 2, 100)

# Выполнение t-критерия Стьюдента
t_stat, p_value, df = ttest_ind(group1, group2)

print(f't-statistic: {t_stat}, p-value: {p_value}, degrees of freedom: {df}')

В примере генерируются синтетические данные для двух групп и, чтобы проверить существенность различий средних этих групп, выполняется t-критерий Стьюдента.

Пример критерия хи-квадрат:

Критерием хи-квадрат определяется, существенна ли связь между двумя категориальными переменными.

from statsmodels.stats.contingency_tables import Table2x2

# Генерирование синтетических данных для таблицы сопряженности 2x2
data = np.array([[20, 15], [10, 30]])

# Выполнение критерия хи-квадрат
table = Table2x2(data)
chi2, p, dof, expected = table.test_nominal_association()

print(f'chi2 statistic: {chi2}, p-value: {p}')

В этом примере генерируются синтетические данные для таблицы сопряженности 2×2 и, чтобы проверить связь между двумя переменными, выполняется критерий хи-квадрат.

Диагностика и оценка моделей

Диагностика моделей важна для проверки допущений статистических моделей и обеспечения их надежности.

Пример диагностики стандартных ошибок коэффициентов линейной регрессии:

import statsmodels.api as sm
import numpy as np
import matplotlib.pyplot as plt

# Генерирование синтетических данных
np.random.seed(0)
X = np.random.rand(100, 1)
X = sm.add_constant(X)
y = 3 + 2 * X[:, 1] + np.random.randn(100)

# Подгонка линейной регрессионной модели
model = sm.OLS(y, X)
results = model.fit()

# Построение графика стандартных ошибок коэффициентов регрессии
residuals = results.resid
plt.figure(figsize=(10, 6))
plt.subplot(2, 1, 1)
plt.plot(residuals, 'o')
plt.title('Residuals')
plt.subplot(2, 1, 2)
sm.qqplot(residuals, line='s')
plt.title('Q-Q Plot')
plt.show()

В этом примере подгоняется модель линейной регрессии, затем строится график стандартных ошибок коэффициентов регрессии, а для оценки их нормальности  —  график «квантиль-квантиль».

Формульный API

В формульном API statsmodels с его строковым синтаксисом формул, аналогичным R, легко задавать статистические модели.

Пример линейной регрессии с формульным API:

import statsmodels.formula.api as smf
import pandas as pd

# Генерирование синтетических данных
np.random.seed(0)
df = pd.DataFrame({
    'X1': np.random.rand(100),
    'X2': np.random.rand(100),
    'Y': 3 + 2 * np.random.rand(100) + np.random.randn(100)
})

# Подгонка линейной регрессионной модели при помощи формульного API
model = smf.ols('Y ~ X1 + X2', data=df)
results = model.fit()

# Сводка результатов регрессии
print(results.summary())

В этом примере генерируются синтетические данные, формульным API подгоняется линейная регрессионная модель, чем упрощается процесс описания модели.

Практический пример: построение прогностической модели

Рассмотрим полный пример построения прогностической модели со statsmodels. На реальном наборе данных продемонстрируем этапы предобработки данных, обучения, оценки и интерпретации модели.

Примерный набор данных и постановка задачи

Воспользуемся набором данных mtcars о характеристиках автомобиля. Цель  —  сделать модель для прогнозирования пробега в милях на галлон по таким параметрам, как мощность, масса и количество цилиндров.

import statsmodels.api as sm
import pandas as pd

# Загрузка набора данных «mtcars»
mtcars = sm.datasets.get_rdataset('mtcars').data

# Отображение первых строк набора данных
print(mtcars.head())

Предобработка данных

Построение модели начинается с предобработки данных. Это обработка пропусков значений, кодирование категориальных переменных и разделение данных на данные для обучения и тестовые данные:

# Проверка пропусков значений
print(mtcars.isnull().sum())

# Кодирование цилиндров «cyl» как категориальной переменной
mtcars['cyl'] = mtcars['cyl'].astype('category')

# Разделение данных на данные для обучения и тестовые данные
from sklearn.model_selection import train_test_split

# Определение независимых переменных — предикторов и зависимой переменной — реакцией
X = mtcars[['hp', 'wt', 'cyl']]
y = mtcars['mpg']

# Добавление свободного члена предикторам
X = sm.add_constant(X)

# Разделение данных
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

Обучение модели

Обучим модель множественной линейной регрессии, используя данные для обучения:

# Подгонка линейной регрессионной модели
model = sm.OLS(y_train, X_train)
results = model.fit()

# Сводка результатов регрессии
print(results.summary())

Оценка модели

Обучив модель, оценим ее производительность на тестовых данных:

# Формирование прогнозов на тестовых данных
y_pred = results.predict(X_test)

# Вычисление метрик оценки
from sklearn.metrics import mean_squared_error, r2_score

mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)

print(f'Mean Squared Error: {mse}')
print(f'R-squared: {r2}')

Интерпретация модели

Интерпретация модели связана с пониманием значимости предикторов и общего соответствия модели.

# Вывод коэффициентов
print(f'Coefficients:\n{results.params}')

# Вывод p-значений
print(f'P-values:\n{results.pvalues}')

# Проверка доверительных интервалов
print(f'Confidence Intervals:\n{results.conf_int()}')

В этом примере мы обучили модель множественной линейной регрессии прогнозировать mpg на основе hp, wt и cyl, оценили производительность модели по среднеквадратической ошибке и коэффициенту детерминации R-квадрат. А также, изучив коэффициенты, p-значения и доверительные интервалы, интерпретировали результаты.

Визуализация результатов

Визуализацией результатов получают дополнительное представление о производительности модели.

import matplotlib.pyplot as plt

# Точечная диаграмма фактических и прогнозных значений
plt.scatter(y_test, y_pred, edgecolors=(0, 0, 0))
plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'k--', lw=4)
plt.xlabel('Actual')
plt.ylabel('Predicted')
plt.title('Actual vs. Predicted MPG')
plt.show()

Этой точечной диаграммой визуализируется соответствие прогнозов модели фактическим значениям.

Заключение

Мы изучили возможности библиотеки statsmodels, мощного инструмента Python для статистического моделирования и проверки гипотез. Рассмотрели целый ряд тем  —  от базовой установки и разведочного анализа данных до продвинутого функционала вроде проверки гипотез и диагностики модели.

Подытожим ключевые моменты

1. Введение в statsmodels: начали с рассмотрения важности статистического моделирования и представили библиотеку statsmodels, подчеркнув ее роль в анализе данных.
2. Приступили к работе с statsmodels: рассказали о процессе установки и структуре библиотеки, продемонстрировав, как осуществляется подгонка простой линейной регрессионной модели.
3. Разведочный анализ данных: обсудили, как выполнять его со statsmodels, включая вычисление количественных показателей распределения и генерирование визуализаций: гистограмм, диаграмм «ящик с усами», точечных диаграмм.
4. Статистические модели в statsmodels: изучили линейную и логистическую регрессии, анализ временны́х рядов ARIMA, обобщенные линейные модели.
5. Продвинутый функционал: рассмотрели проверку гипотез, диагностику моделей и формульный API, продемонстрировав, как выполняются t-критерии Стьюдента, критерий хи-квадрат и диагностика стандартных ошибок коэффициентов для моделей линейной регрессии.
6. Практический пример построения прогностической модели: с набором данных mtcars, включая предобработку данных, обучение, оценку и интерпретацию модели.

Преимущества statsmodels

• Комплексные статистические инструменты: в statsmodels имеются разнообразные статистические модели и тесты, это универсальное решение для статистического анализа на Python.
• Простота применения: формульным API упрощается описание статистических моделей, поэтому statsmodels доступна даже для пользователей, знакомых с R.
• Интеграция с другими библиотеками: Python, такими как Pandas, Matplotlib и Seaborn. Так что statsmodels пригодится в рабочих процессах анализа данных.

Дополнительные ресурсы

• Официальная документация по statsmodels: с полным описанием всего функционала с примерами.
• Руководство по науке о данных Python Джейка Вандерпласа: с главами об анализе данных и статистическом моделировании на Python.
• Курсы Coursera по науке о данных: с углубленным обучением статистическому моделированию и анализу данных на Python.

Включив statsmodels в свой инструментарий для анализа данных, вы сможете использовать его мощные статистические возможности для проведения тщательного анализа, принятия обоснованных решений и извлечения значимой информации из данных.

Не забывайте всегда самостоятельно изучать и проверять получаемую информацию. Полагаться исключительно на других  —  значит применять устаревшие или некорректные практики. Проявляйте инициативу: реализуйте и дорабатывайте найденный код под конкретные требования и стандарты.

Читайте также:

• 20 Python-скриптов для автоматизации повседневных задач
• Шаблоны проектирования Python: рекомендации и антипаттерны
• Сервис балансировки нагрузки на ПИД-регуляторах — умозрительный пример

Читайте нас в Telegram, VK и Дзен

---

Перевод статьи CyCoderX: Unlocking Python’s Statsmodels: A Comprehensive Guide