Разное

Регрессор дерева решений

31.01.2025

Применение деревьев решений не ограничиваются категоризацией данных. Эта модель также эффективна для прогнозирования числовых значений! Классификационные деревья часто привлекают к себе внимание, но регрессоры деревьев решений (или регрессионные деревья) являются мощными и универсальными инструментами в мире прогнозирования непрерывных переменных.

В этой статье, уделив внимание механизму создания регрессионного дерева (который в основном схож с построением классификационного дерева), выйдем за рамки методов предварительной обрезки, таких как «минимальный лист выборки» и «максимальная глубина дерева». Рассмотрим наиболее распространенный метод последующей обрезки — обрезку с учетом сложности/стоимости, которая вводит параметр сложности в функцию потерь дерева решений.

Все визуализации созданы автором с помощью Canva Pro и оптимизированы для мобильных устройств (на десктопных компьютерах могут выглядеть увеличенными).

Определение

Дерево решений для регрессии — модель, которая предсказывает числовые значения с помощью древовидной структуры. Она разбивает данные по ключевым признакам, начиная с корневого вопроса и затем разветвляясь. Каждый узел спрашивает о признаке, разделяя данные еще больше, пока не достигнет листовых узлов с окончательными предсказаниями. Чтобы получить результат, нужно пройти по пути, соответствующему характеристикам данных, от корня к листьям.

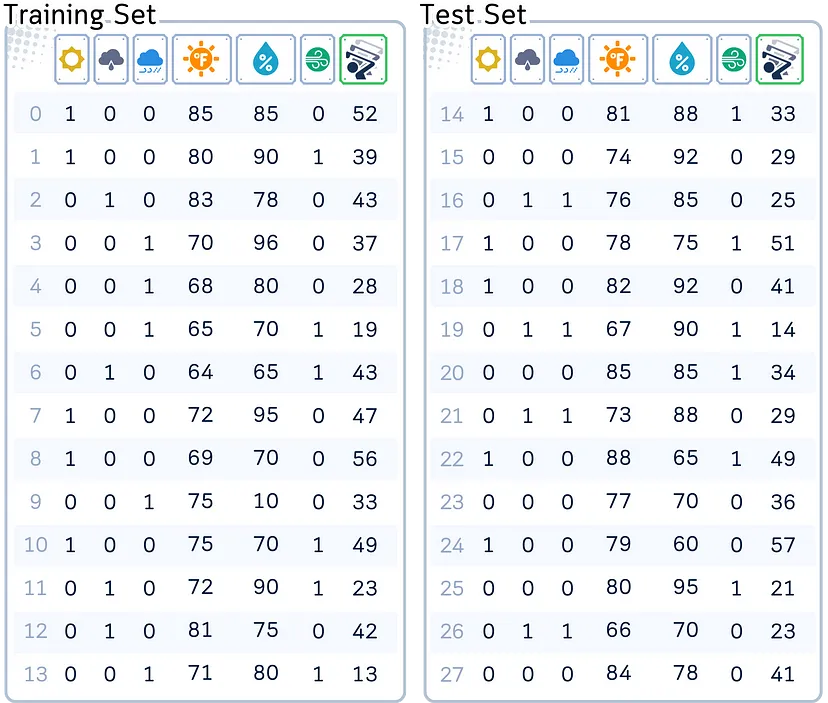
Деревья решений для регрессии предсказывают числовые результаты, следуя ряду вопросов, основанных на данных, и сводя их к окончательному значению.

Используемый набор данных

В демонстрационных целях будем работать со стандартным набором данных. Этот набор данных используется для прогнозирования количества игроков в гольф (number of players), посещающих поле в определенный день, и включает такие переменные, как прогноз погоды (weather outlook), температура (temperature), влажность (humidity) и ветер (wind).

Столбцы: «Прогноз» (быстрое кодирование: солнечно, пасмурно, дождь), «Температура» (в градусах по Фаренгейту), «Влажность» (в %), «Ветер» (да/нет) и «Количество игроков» (числовая целевая характеристика).

import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split

# Создание набора данных
dataset_dict = {
    'Outlook': ['sunny', 'sunny', 'overcast', 'rain', 'rain', 'rain', 'overcast', 'sunny', 'sunny', 'rain', 'sunny', 'overcast', 'overcast', 'rain', 'sunny', 'overcast', 'rain', 'sunny', 'sunny', 'rain', 'overcast', 'rain', 'sunny', 'overcast', 'sunny', 'overcast', 'rain', 'overcast'],
    'Temp.': [85.0, 80.0, 83.0, 70.0, 68.0, 65.0, 64.0, 72.0, 69.0, 75.0, 75.0, 72.0, 81.0, 71.0, 81.0, 74.0, 76.0, 78.0, 82.0, 67.0, 85.0, 73.0, 88.0, 77.0, 79.0, 80.0, 66.0, 84.0],
    'Humid.': [85.0, 90.0, 78.0, 96.0, 80.0, 70.0, 65.0, 95.0, 70.0, 80.0, 70.0, 90.0, 75.0, 80.0, 88.0, 92.0, 85.0, 75.0, 92.0, 90.0, 85.0, 88.0, 65.0, 70.0, 60.0, 95.0, 70.0, 78.0],
    'Wind': [False, True, False, False, False, True, True, False, False, False, True, True, False, True, True, False, False, True, False, True, True, False, True, False, False, True, False, False],
    'Num_Players': [52, 39, 43, 37, 28, 19, 43, 47, 56, 33, 49, 23, 42, 13, 33, 29, 25, 51, 41, 14, 34, 29, 49, 36, 57, 21, 23, 41]
}

df = pd.DataFrame(dataset_dict)

# Быстрое кодирование столбца 'Outlook' 
df = pd.get_dummies(df, columns=['Outlook'],prefix='',prefix_sep='')

# Преобразование столбца 'Wind' в двоичный формат
df['Wind'] = df['Wind'].astype(int)

# Разделение данных на признаки и цель, а затем на обучающий и тестовый наборы
X, y = df.drop(columns='Num_Players'), df['Num_Players']
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.5, shuffle=Fals

Основной механизм

Дерево решений для регрессии работает путем рекурсивного разделения данных на основе признаков, которые наилучшим образом уменьшают ошибку предсказания. Вот общий процесс:

Начинаем со всего набора данных в корневом узле.

Выбираем признак, который минимизирует определенную метрику ошибки (например, среднюю квадратичную ошибку или дисперсию), чтобы разделить данные.

Создаем дочерние узлы на основе разбиения, где каждый дочерний узел представляет собой подмножество данных, выровненных по соответствующим значениям признака.

Повторяем этапы 2-3 для каждого дочернего узла, продолжая разбивать данные до тех пор, пока не будет достигнуто условие остановки.

Присваиваем окончательное прогнозируемое значение каждому узлу листа — обычно среднее целевых значений в данном узле.

Этапы обучения

Рассмотрим регрессионную часть в алгоритме дерева решений CART (classification and regression trees — деревья классификации и регрессии). Она отвечает за создание двоичных деревьев с прохождением следующих этапов:

1. Начинаем со всех обучающих образцов в корневом узле.

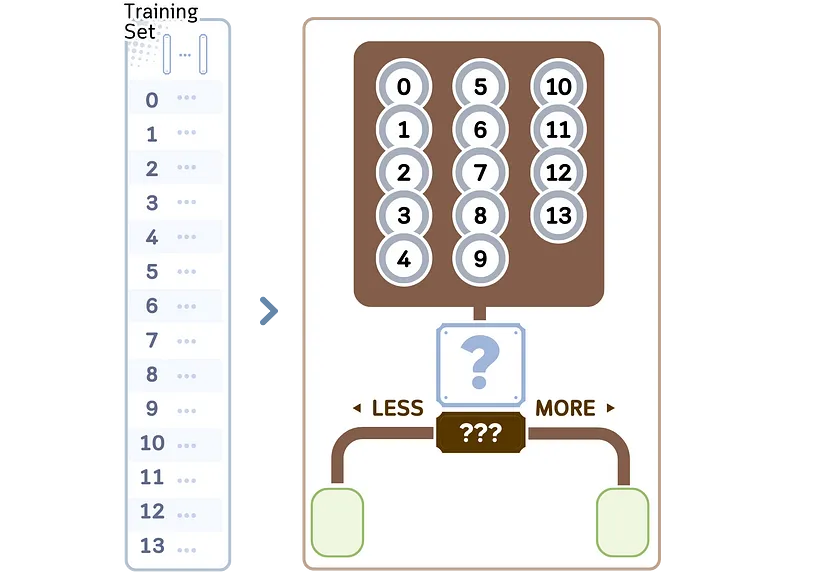
2. По каждому признаку в наборе данных:

a) сортируем значения признаков в порядке возрастания;

b) рассматриваем все средние точки между соседними значениями как потенциальные точки разделения (split points).

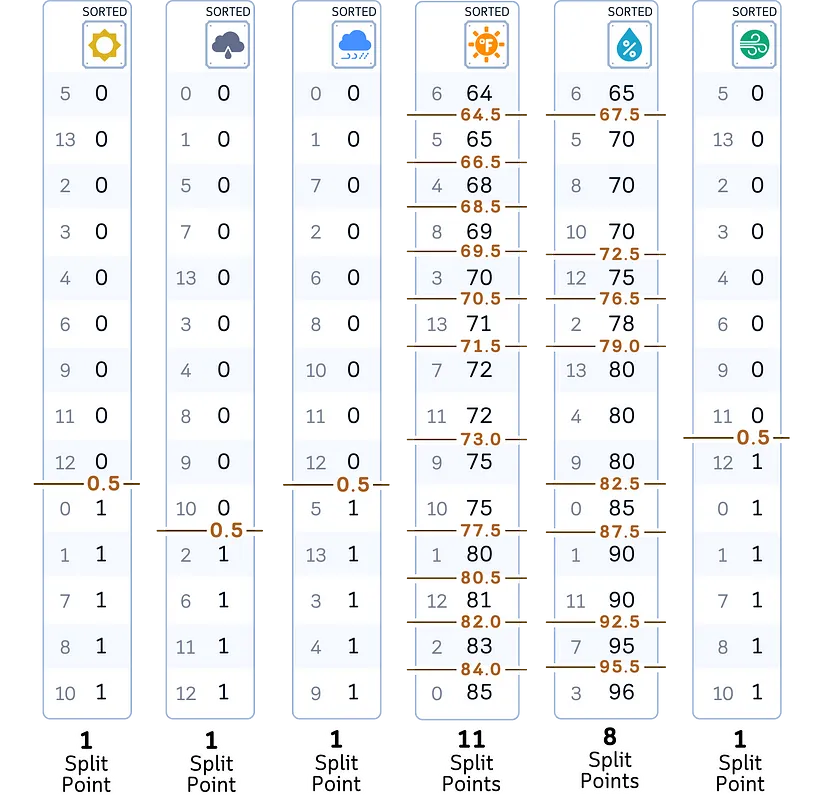
Всего нужно проверить 23 точки разделения.

3. Для каждой потенциальной точки разделения:

a) рассчитываем среднеквадратичную ошибку (MSE) для текущего узла;

b) вычисляем средневзвешенное значение ошибок для результирующего разбиения.

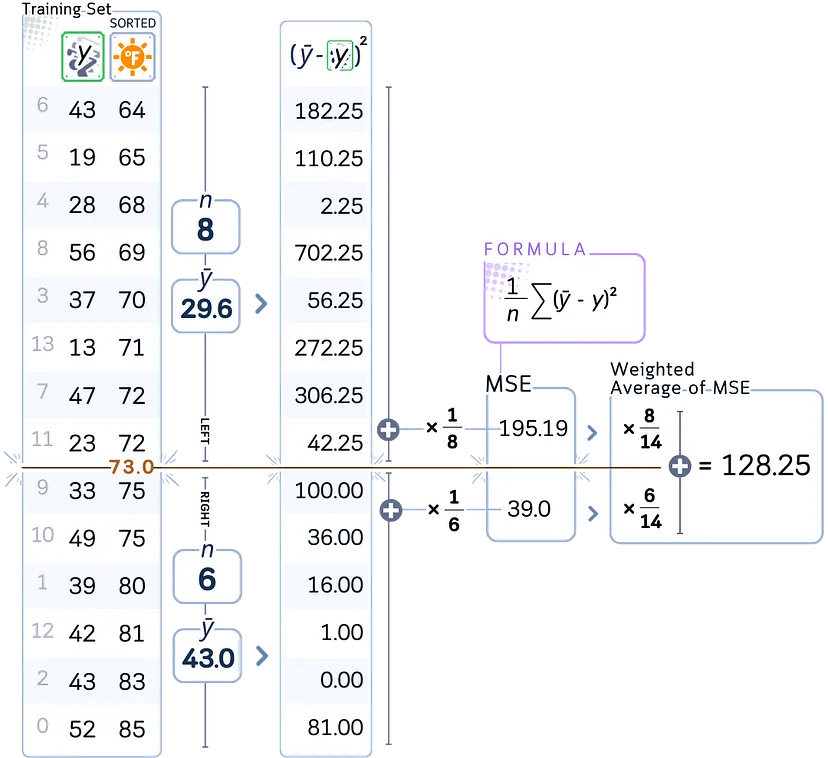
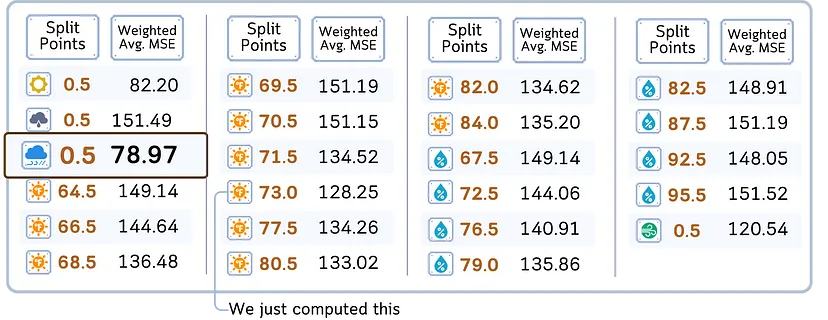
В качестве примера приведен расчет средневзвешенного значения MSE для точки разделения «Температура» со значением 73,0.

4. После оценки всех функций и точек разделения выбираем ту, которая имеет наименьшее средневзвешенное значение MSE.

5. Создаем два дочерних узла на основе выбранного признака и точки разделения:

левый дочерний узел: образцы со значением признака <= точка разделения;

правый дочерний узел: образцы со значением признака > точка разделения.

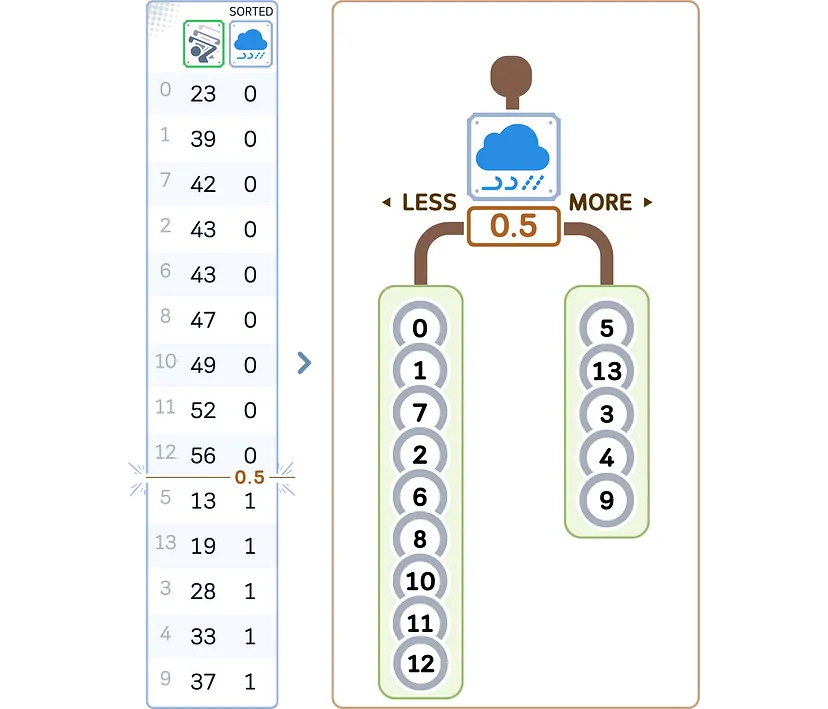
6. Рекурсивно повторяем этапы 2-5 для каждого дочернего узла. (Продолжаем до тех пор, пока не будет достигнут критерий остановки).

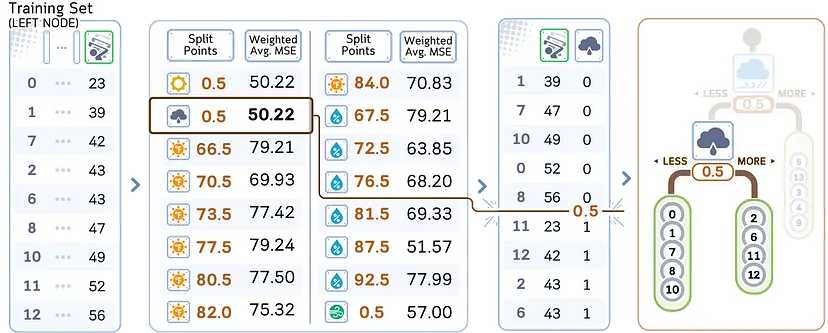
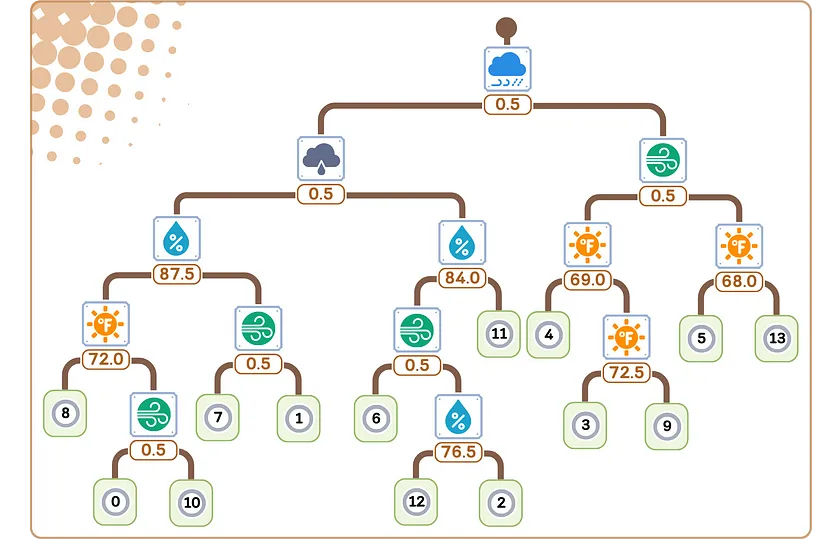
7. В каждом листовом узле в качестве прогноза назначаем среднее целевое значение образцов в этом узле.

from sklearn.tree import DecisionTreeRegressor, plot_tree
import matplotlib.pyplot as plt

# Обучение модели
regr = DecisionTreeRegressor(random_state=42)
regr.fit(X_train, y_train)

# Визуализация дерева решений
plt.figure(figsize=(26,8))
plot_tree(regr, feature_names=X.columns, filled=True, rounded=True, impurity=False, fontsize=16, precision=2)
plt.tight_layout()
plt.show()

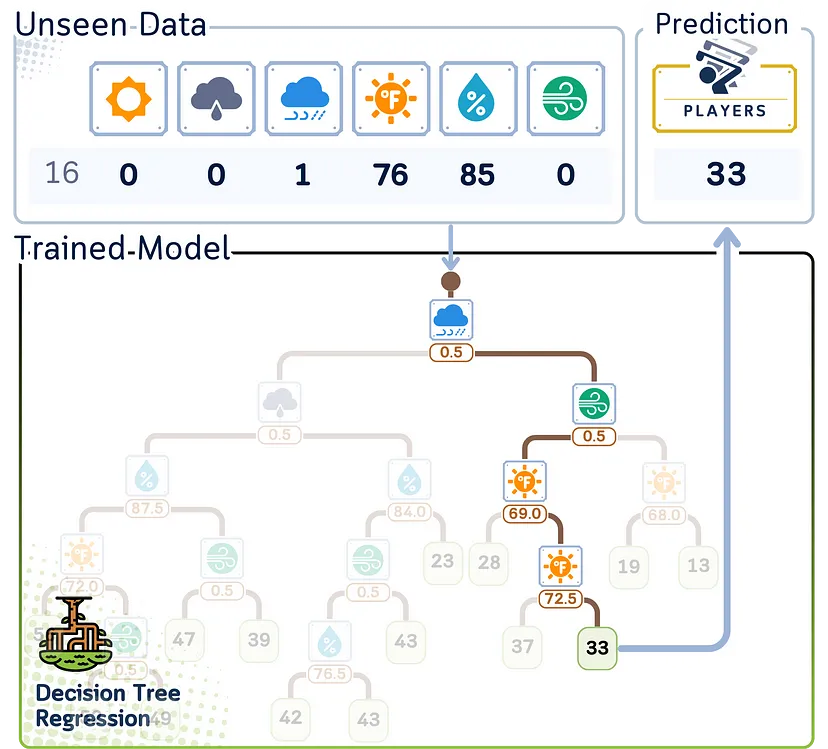
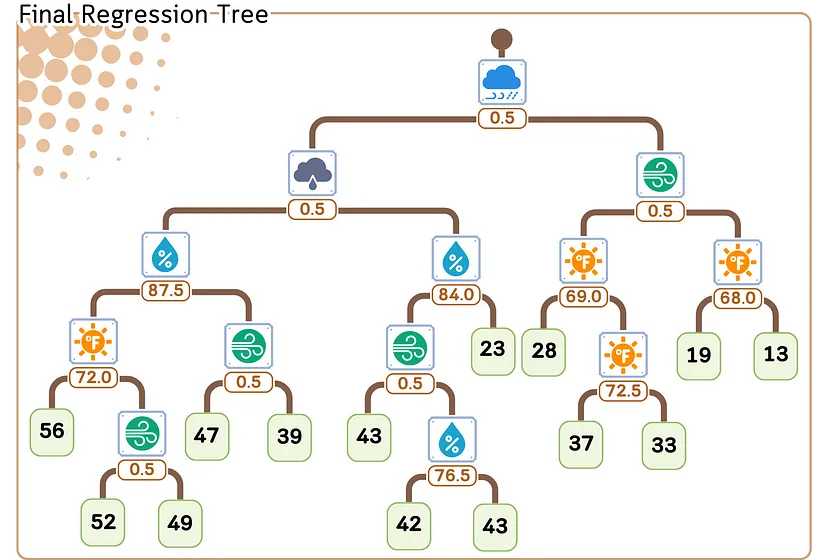
В этом выводе scikit-learn показаны образцы и значения для листовых и промежуточных узлов.

Этап регрессии/прогнозирования

Вот как дерево регрессии делает предсказания для новых данных:

1. Начинаем с вершины (корня) дерева.

2. В каждой точке принятия решения (узле):

смотрим на значение признака и разделения;

если значение признака точки данных меньше или равно, двигаемся влево;

если больше, переходим вправо.

3. Продолжаем двигаться вниз по дереву, пока не достигнем конца (листа).

4. Прогноз — среднее значение, хранящееся в этом листе.

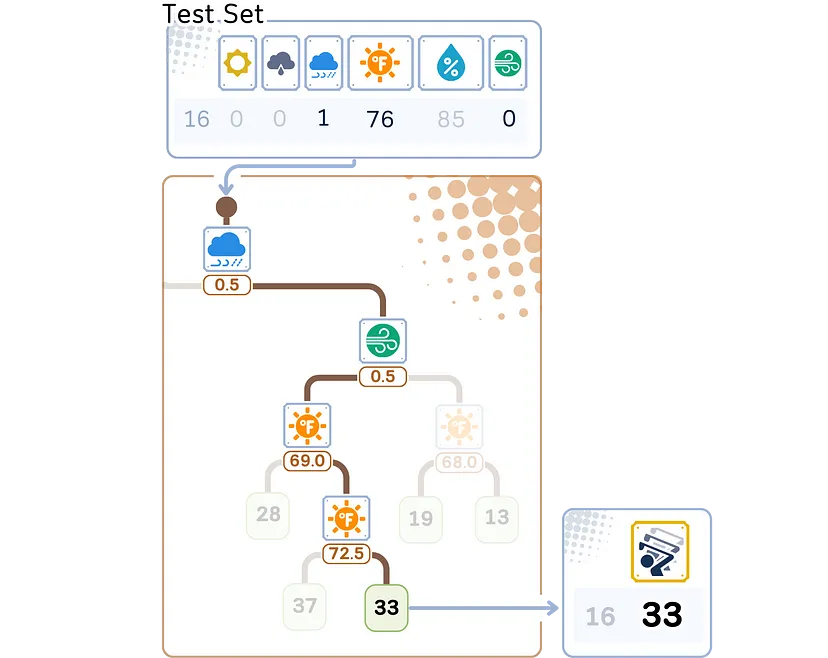
Этап оценки

Это значение RMSE намного лучше, чем результат фиктивного регрессора.

Предварительная и последующая обрезки

После построения дерева единственное, о чем нужно беспокоиться, — это о методе уменьшения его размера для предотвращения переобучения. Метод обрезки включает предварительную и последующую обрезки.

Предварительная обрезка

Предварительная обрезка (pre-pruning), также известная как ранняя остановка, подразумевает остановку роста дерева решений в процессе обучения на основе определенных заранее критериев. Этот подход направлен на предотвращение излишней сложности дерева, чтобы оно не перестало соответствовать обучающим данным. К распространенным техникам предварительной обрезки относятся:

Максимальная глубина (maximum depth): ограничение глубины роста дерева.

Минимальное количество образцов для разбиения (minimum samples for split): требование минимального количества образцов для обоснования разбиения узла.

Минимальное количество образцов на лист (minimum samples per leaf): обеспечение того, чтобы каждый листовой узел имел по крайней мере определенное количество образцов.

Максимальное количество узлов листа (maximum number of leaf nodes): ограничение общего числа листовых узлов в дереве.

Минимальное уменьшение примесей (minimum impurity decrease): разрешение только тех разделений, которые уменьшают примесь (включения) на заданную величину.

Эти техники останавливают рост дерева при выполнении заданных условий, эффективно «обрезая» дерево на этапе его создания.

Последующая обрезка

Последующая обрезка (post-pruning), напротив, позволяет дереву решений разрастаться в полную силу, а затем обрезается для снижения сложности. При таком подходе сначала создается полное дерево, а затем удаляются или сворачиваются ветви, которые не вносят существенного вклада в производительность модели. Одна из распространенных техник последующей обрезки называется обрезкой с учетом сложности и потерь (cost-complexity pruning).

Обрезка с учетом сложности и потерь

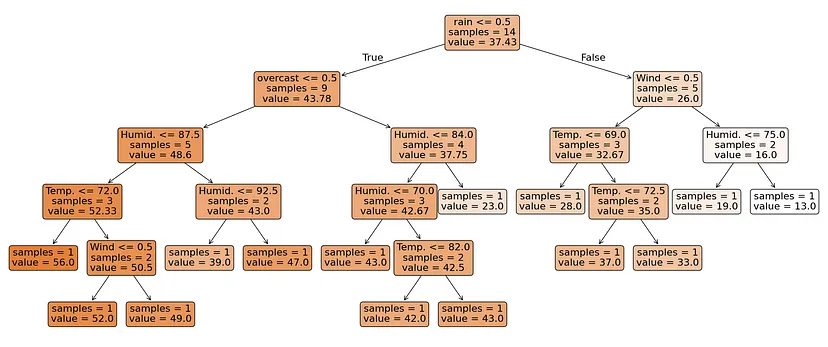
Этап 1: Вычисляем примесь для каждого узла

Для каждого промежуточного узла вычисляем примесь (MSE для случая регрессии). Затем сортируем это значение от наименьшего к наибольшему.

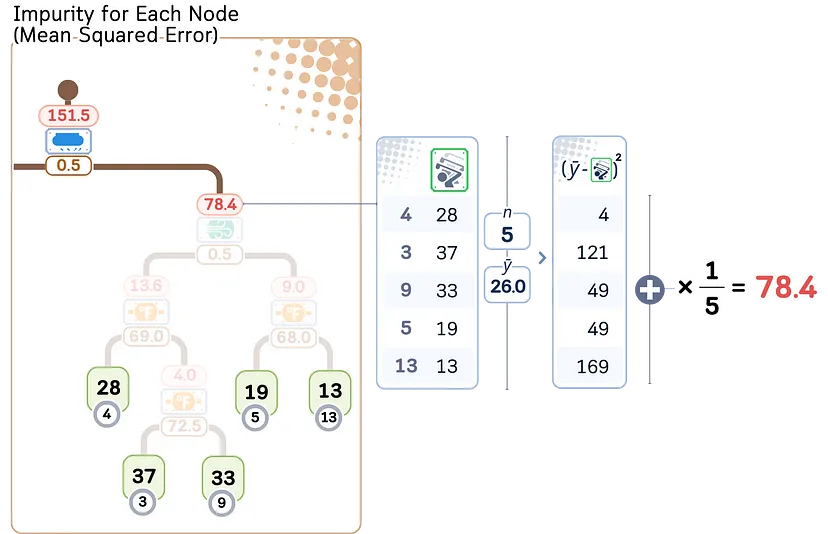
# Визуализация дерева решений
plt.figure(figsize=(26,8))
plot_tree(regr, feature_names=X.columns, filled=True, rounded=True, impurity=True, fontsize=16, precision=2)
plt.tight_layout()
plt.show()

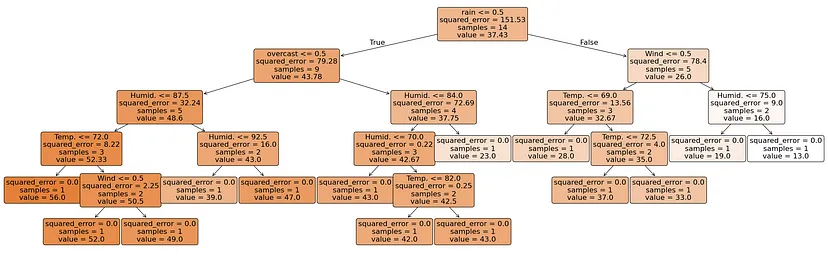
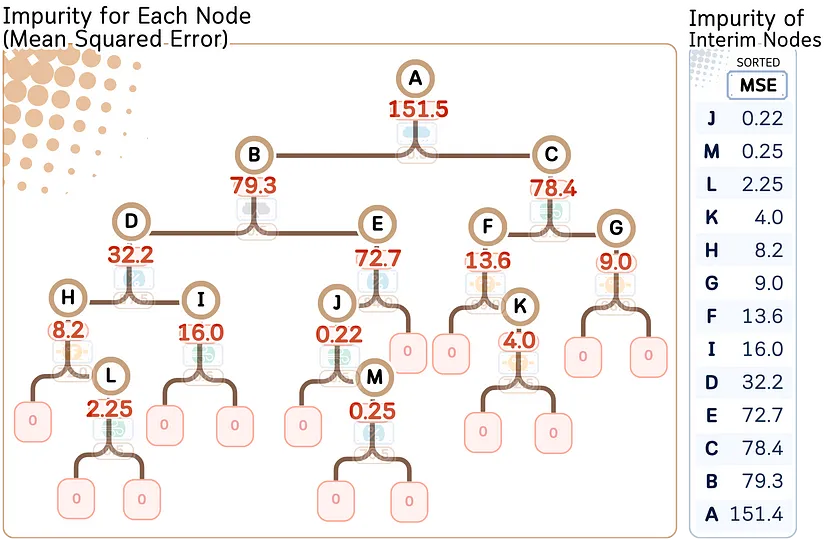
В этом выводе scikit-learn примеси показаны как «squared_error» для каждого узла.

Даем названия этим промежуточным узлам (от A до J). Затем сортируем их по их MSE от наименьшего к наибольшему.

Этап 2: Создание поддеревьев путем обрезки самого слабого звена

Цель этого этапа — постепенно превратить промежуточные узлы в листья, начиная с узла с наименьшим MSE (= слабая связь). На основе этого можно создать путь обрезки.

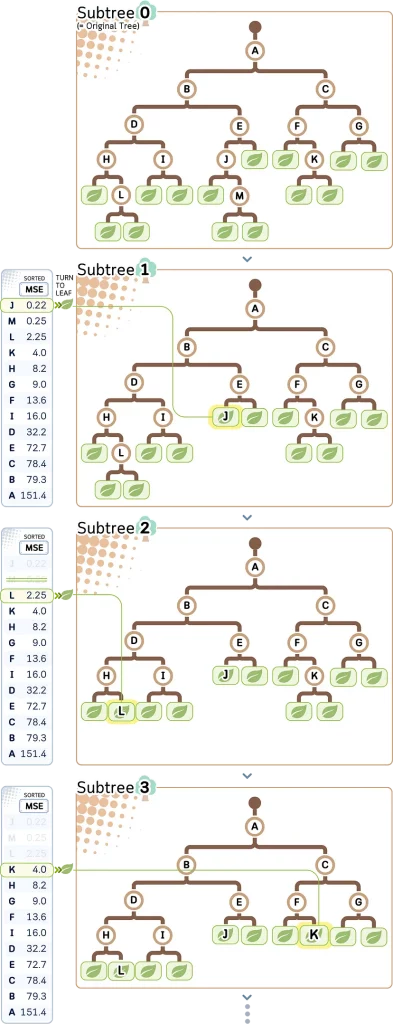
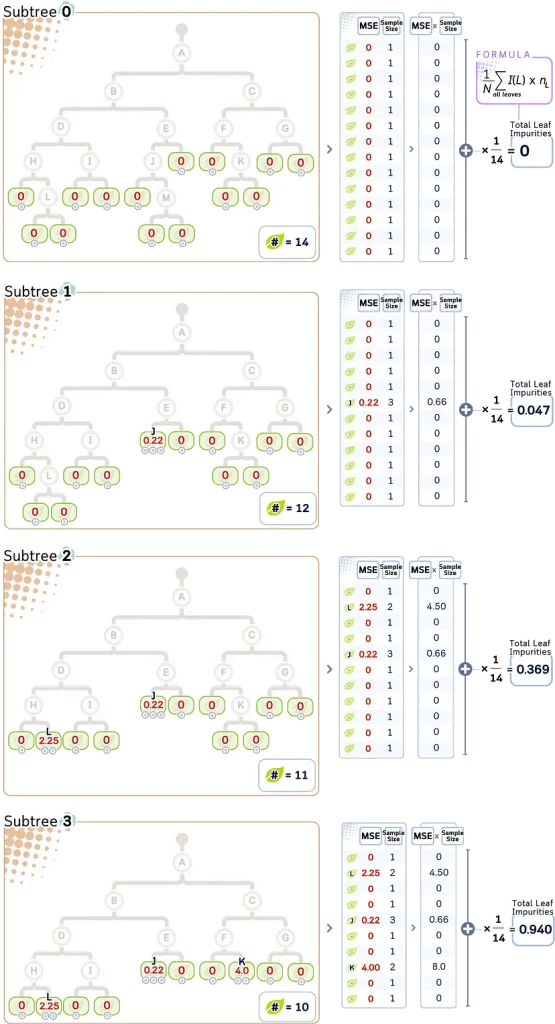
Назовем каждое из них «Поддерево i» («Subtree i») в зависимости от того, сколько раз (i) оно подвергается обрезке. Начиная с исходного дерева, дерево будет обрезано на узлах с наименьшим MSE (начиная с узла J, M (уже обрезанный J), L, K и так далее).

Шаг 3: Рассчитываем общее количество примесей в листьях для каждого поддерева

Для каждого поддерева (subtree T) общее количество примесей листьев (R(T)) может быть рассчитано следующим образом:

R(T) = (1/N) Σ I(L) * n_L

где:

L — диапазон всех узлов листьев;

n_L — количество образцов в листе L;

N — общее количество образцов в дереве;

I(L) — примесь (MSE) листа L.

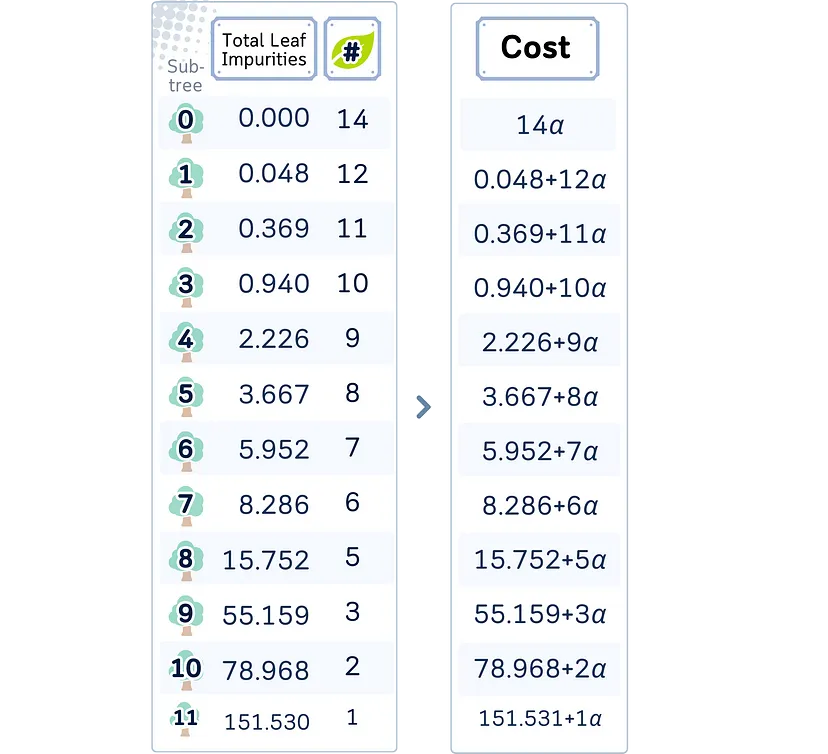
Чем больше обрезаем, тем выше общее количество примесей в листьях.

Этап 4: Вычисление функции потерь

Чтобы контролировать, когда прекратить превращение промежуточных узлов в листья, сначала проверяем сложность и потери для каждого поддерева (subtree T) по следующей формуле:

Cost(T) = R(T) + α * |T|

где:

R(T) — общее количество примесей листьев;

|T| — количество узлов листьев в поддереве;

α — коэффициент сложности.

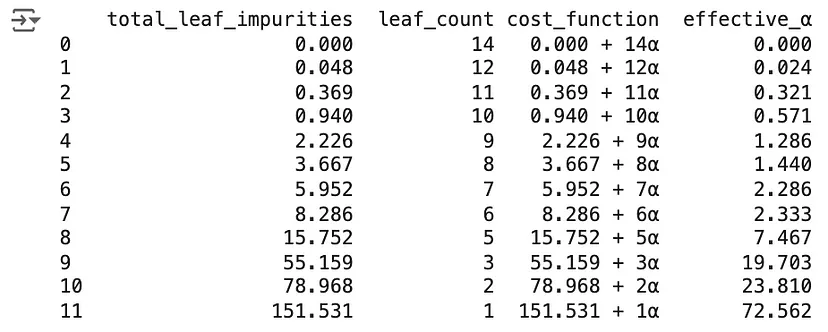
Этап 5: Выбираем коэффициент α

Значение α определяет, какое поддерево получим в итоге. Поддерево с наименьшими потерями будет конечным деревом.

Когда значение α мало, больше заботимся о точности (большие деревья). Когда значение α велико, больше заботимся о простоте (меньшие деревья).

Хотя можно свободно задавать значение α, scikit-learn позволяет также вычислить наименьшее значение α для получения определенного поддерева. Оно называется эффективным значением α.

# Вычисление пути обрезки с учетом сложности и стоимости
tree = DecisionTreeRegressor(random_state=42)
effective_alphas = tree.cost_complexity_pruning_path(X_train, y_train).ccp_alphas
impurities = tree.cost_complexity_pruning_path(X_train, y_train).impurities

# Функция для подсчета узлов листьев
count_leaves = lambda tree: sum(tree.tree_.children_left[i] == tree.tree_.children_right[i] == -1 for i in range(tree.tree_.node_count))

# Обучение деревьев и подсчет листьев для каждого параметра сложности
leaf_counts = [count_leaves(DecisionTreeRegressor(random_state=0, ccp_alpha=alpha).fit(X_train_scaled, y_train)) for alpha in effective_alphas]

# Создание DataFrame с результатами анализа
pruning_analysis = pd.DataFrame({
    'total_leaf_impurities': impurities,
    'leaf_count': leaf_counts,
    'cost_function': [f"{imp:.3f} + {leaves}α" for imp, leaves in zip(impurities, leaf_counts)],
    'effective_α': effective_alphas
})

print(pruning_analysis)

Заключительные замечания

Методы предварительной обрезки, как правило, быстрее и экономнее в плане памяти, так как не позволяют дереву вырасти слишком большим.

Последующая обрезка потенциально может создавать более оптимальные деревья, поскольку рассматривает всю структуру дерева перед принятием решений об обрезке. Однако она может быть более затратной с точки зрения вычислений.

Оба подхода направлены на поиск баланса между сложностью модели и ее производительностью с целью создания модели, которая способна к эффективному обобщению на уровне невидимых данных. Выбор между предварительной и последующей обрезкой (или их сочетанием) часто зависит от конкретного набора данных, поставленной задачи и, конечно, доступных вычислительных ресурсов.

На практике часто используют комбинацию этих методов, например, применяют некоторые критерии предварительной обрезки для предотвращения слишком больших деревьев, а затем используют последующую обрезку для тонкой настройки сложности модели.