5 базовых статистических концептов, которые должен знать каждый специалист по обработке данных

В таком искусстве, как наука о данных, статистика может оказаться мощным инструментом. В широком смысле, статистика означает использование математики для технического анализа данных. Базовая визуализация, например, гистограмма, может быть очень информатична, но с помощью статистики мы получаем гораздо больше точных данных. И математические вычисления дают не примерную оценку, а конкретные выводы о данных.

Статистика позволяет нам получать более глубокую и детальную информацию о том, как устроены наши данные. Исходя из этого строения, мы можем оптимально использовать другие методы науки о данных, чтобы получить еще больше информации. В этой статье мы рассмотрим 5 базовых концептов, которые должен знать каждый специалист по обработке данных, и поговорим о том, как использовать их максимально эффективно!

Описательная статистика

Описательная статистика является наиболее используемым статистическим концептом в науке о данных. При исследовании данных в первую очередь используют именно ее, включая следующие параметры: смещение, дисперсию, среднее значение, медиану, процентили и другие. Все указанное легко понять и осуществить в коде! Посмотрите на график ниже в качестве иллюстрации.

Базовая диаграмма “ящик с усами”:

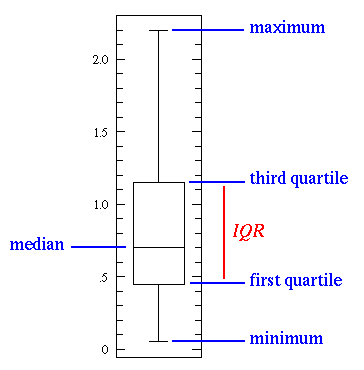
Линия по середине — это значение медианы данных. Правильнее использовать именно ее, а не среднее значение, из-за ее устойчивости к выбросам. Первый квартиль равен 25% процентилям, то есть 25% точек выборки находятся ниже этого значения. Третий квартиль равен 75% процентилям, то есть 75% точек выборки находятся ниже этого значения. Минимальное и максимальное значения являются верхней и нижней границами нашего диапазона данных.

Диаграмма “ящик с усами” идеально иллюстрирует информацию, получаемую с помощью описательной статистики:

• Если ящик с усами короткий, то это значит, что большинство точек данных похожи, так как мы имеем много значений в маленьком диапазоне
• Если ящик с усами длинный, то это значит, что большинство точек выборки отличаются, так как значения распространены в широком диапазоне
• Если значение медианы ближе к нижнему квартилю, то большая часть данных имеет низкое значение. Если значение медианы ближе к верхнему квартилю, то большая часть данных имеет высокое значение. Иначе говоря, если линия медианы находится не в центре ящика, то это является показателем того, что данные асимметричны.
• А если усы очень длинные? То это значит, что данные имеют высокую степень разброса среднеквадратичного отклонения и дисперсии. То есть, значения сильно распространены и имеют явные отличия. Если усы длинные только на одной стороне, то данные могут сильно отличаться только в одном направлении.

Всю эту информацию мы получили из нескольких легко вычислимых описательных статистик! Используйте их всегда, когда вам необходимо получить быстрый, но информативный вывод о данных.

Распределение вероятностей

Вероятность выражает то, насколько возможно конкретное событие. В науке о данных вероятность оценивается значениями от 0 до 1. 0 означает уверенность в том, что определенное событие не произойдет, а 1 — произойдет. Распределение вероятностей — это функция, показывающая вероятность всех возможных значений в эксперименте. Посмотрите на график ниже в качестве иллюстрации.

Распространенные распределения вероятностей. Непрерывное, нормальное, Пуассона:

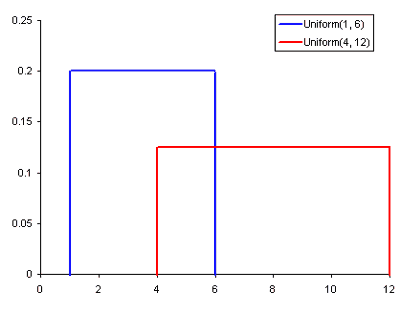
• Непрерывное равномерное распределение является самым базовым распределением из трех нами рассматриваемых. Оно имеет одно единственное значение, которое есть в определенном диапазоне, а все остальное, что находится вне этого диапазона, равно 0. Вполне себе “включает/ не включает” распределение. Также можно представить данное распределение как указатель категориальной переменной с двумя категориями: 0 или значение. У категориальной переменной может быть несколько значений кроме 0, но мы все равно можем представить ее в виде кусочной функции с несколькими равномерными распределениями.
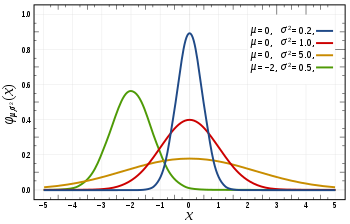
• Нормальное распределение или распределение Гаусса определяется своим среднеарифметическим значением и среднеквадратичным отклонением. Среднеарифметическое значение сдвигает распределение пространственно, а среднеквадратичное отклонение контролирует это распределение. Главное отличие нормального распределения от других (например, Пуассона) заключается в том, что в нем среднеквадратичное отклонение одинаково во всех направлениях. Таким образом, с помощью распределения Гаусса можно узнать среднее значение набора данных, так же как и распространение данных. Иными словами, мы можем узнать распространены ли данные в широком диапазоне или сконцентрированы вокруг нескольких значений.
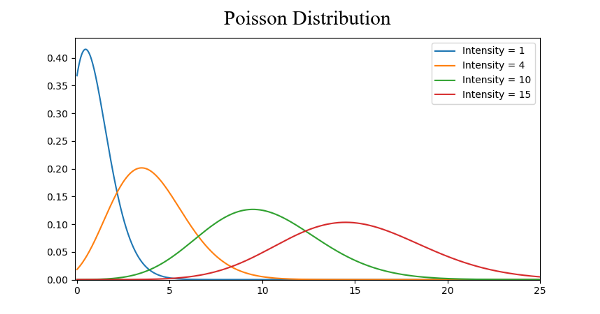
• Распределение Пуассона похоже на нормальное, но оно имеет еще один фактор — асимметрию. У распределения Пуассона при низком значении асимметрии будет сравнительно равномерное распределение во всех направлениях, как и у нормального. Но если значение асимметрии будет высоким по величине, то распространение данных будет разным во всех направлениях: в одном направлении распределение будет сильно распространено, а в другом — высоко сконцентрировано.

Существует намного больше распределений, но этих трех будет вполне достаточно. Мы можем быстро увидеть и понять категориальные переменные благодаря непрерывному равномерному распределению. А если перед нами распределение Гаусса, то мы знаем, что существует много алгоритмов, которые по умолчанию будут хорошо с ним работать. Про распределение Пуассона мы знаем, что оно требует особенного обращения и такого алгоритма, который будет устойчивым к изменениям в пространственном распространении.

Снижение размерности

Термин “снижение размерности” интуитивно понятен. У нас есть какой-то набор данных, в котором мы хотим сократить количество размерностей. В науке о данных это количество признаковых переменных. Посмотрите на график ниже в качестве иллюстрации.

Снижение размерности:

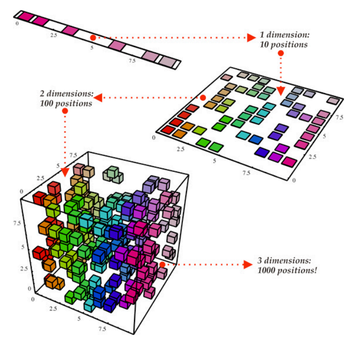
Куб является нашим набором данных и имеет три размерности с 1000 точек. С современными вычислительными системами обработка 1000 точек не составит труда, но с большим количеством у нас появятся проблемы. Хотя, если посмотреть на наш набор данных с двухмерной стороны, например, с одной стороны куба, то мы увидим, что, цвета распределить не сложно. При снижении размерности, мы проецируем 3D данные на двухмерную плоскость. Такой способ эффективно сократит количество вычисляемых точек до 100. Какая экономия!

Еще один способ снижения размерности — сокращение по признаку. Сокращение по признаку означает удаление тех признаков, которые являются несущественными для анализа. Например, после исследования набора данных обнаруживается, что 7 признаков из 10 имеют в результате высокую корреляцию, а другие 3 — очень низкую. Тогда эти 3 признака, скорее всего, будут неважными для вычисления и их можно убрать из анализа без влияния на результат.

Наиболее распространенной статистической техникой для снижения размерности является PCA (метод главных компонент), которая создает векторные представления признаков, показывая, насколько они важны для результата, т.е. для их корреляции. PCA можно использовать для обоих методов снижения размерности, указанных выше. Подробнее о PCA читайте здесь.

Недостаточная выборка и выборка с запасом

Недостаточная выборка и выборка с запасом являются техниками, используемыми для задач классификации. Бывает так, что набор данных классификации может быть слишком наклонен в одну сторону. Например, у нас есть 2000 примеров для класса 1 и всего лишь 200 для класса 2. Из-за этого могут возникнуть проблемы со многими методами машинного обучения, которые мы пытаемся использовать для моделирования данных и прогнозирования! И тогда на помощь приходят недостаточная выборка и выборка с запасом. Посмотрите на график ниже в качестве иллюстрации.

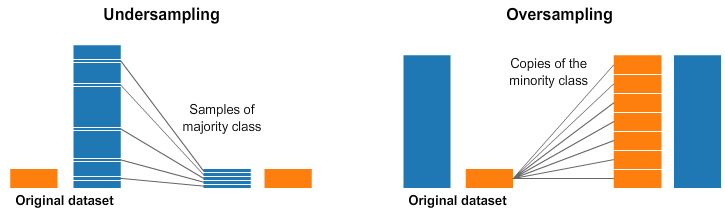
На правой и левой картинках у голубого класса гораздо больше примеров, чем у оранжевого. И поэтому мы используем два параметра предварительной обработки, которые помогут в подготовке моделей машинного обучения.

Недостаточная выборка означает, что нужно выбрать только некоторыеданные из мажоритарного класса, используя ровно столько примеров, сколько есть в миноритарном классе. Такой отбор необходимо сделать для того, чтобы сохранить распределение вероятностей класса. Все просто! Мы выровняли набор данных, выбрав меньше примеров!

Выборка с запасом означает, что нужно создать копии миноритарного класса для того, чтобы получить такое же количество примеров, как и в мажоритарном классе. Копии будут созданы с сохранением распределения миноритарного класса. И вот мы выровняли набор данных без добавления новых данных!

Байесовская статистика

Чтобы понять, зачем нужна Байесовская статистика, необходимо сначала понять, где не работает частотная статистика. Частотная статистика — это тип статистики, с которым часто ассоциируется слово “вероятность”. Она заключается в использовании математики для анализа вероятности какого-либо события, где вычисляются только предварительные данные.

К примеру: представим, что я дал вам игральную кость и спросил, какова вероятность, что выпадет число 6. Многие скажут, что вероятность составляет 1 к 6. И действительно, если бы мы производили частотный анализ, мы бы посмотрели на данные, которые показывали, как кто-то бросил кость 10,000 раз, и вычислили бы частотность каждого выпавшего числа. Вот мы и получаем вероятность 1 к 6!

А если бы вам сказали, что игральная кость утяжелена так, чтобы всегда выпадало число 6? Так как частотный анализ берет в расчет только предварительные данные, то, соответственно, он не включает тот факт, что кость может быть утяжелена.

Байесовская статистика этот факт рассматривает. Проиллюстрируем этот пример исходя из Байесовской теоремы:

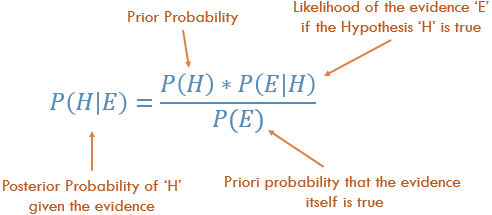
Вероятность P(H) в уравнении является частотным анализом, который учитывает предварительные данные вероятности нашего события. P(E|H) — возможность, т.е. вероятность того, что факт является правильным, учитывая информацию из частотного анализа. Например, если вы хотели кинуть кость 10,000 раз, и в первые 100 раз выпало число 6, то тогда, вы были бы уверенны в том, что кость утяжелена! P(E) является вероятностью того, что факт является правдой. Если бы я вам сказал, что кость утяжелена, вы бы поверили мне или подумали, что я вас обманываю?!

Если частотный анализ показывает правильный результат, то он имеет какие-то основания в подтверждении нашей догадки. В то же время мы учитываем тот факт, что кость может быть утяжелена, основываясь как на предварительном, так и на частотном анализе. Как видно из примера, Байесовская статистика учитывает абсолютно все. Используйте ее, когда кажется, что предварительных данных недостаточно.

Перевод статьи George Seif: The 5 Basic Statistics Concepts Data Scientists Need to Know