Сумасшедший способ проверить, является ли число простым, используя регулярное выражение

В поисках алгоритмов для выявления простых чисел, вы где-нибудь, да встречали подобное выражение:

Что это? Это способ проверки, является ли число простым. Вам даже не придётся писать цикл for!

Дико, не так ли?

Я тоже так думал. Поэтому решил, что будет интересно разобрать и разъяснить это выражение шаг за шагом на случай, если кому-то любопытно.

Примечание: Я знаю, регулярные выражения иногда похожи на абракадабру (особенно, всё что между символами /), но я обещаю, что всё обретёт смысл. Оставайтесь со мной.

Так что же здесь происходит?

В целом, суть функции сводится к трём шагам:

1. Привести число к его унарной форме

2. Проверить, является ли оно 0 или 1

3. Проверить, является ли оно кратным любому числу больше 1

Шаг №1

Во-первых, нам нужно привести проверяемое число в унарную форму. Унарную систему можно представить как счёт на палочках (т.е. 3 записывается как «111», а 4 как «1111» и т.д.).

За это отвечает данный кусок кода:

Этот код создаёт массив с n + 1 пустыми слотами, далее присоединяет к этим пустым значениям — единицы.

Я предпочитаю использовать метод String.prototype.repeat() из ES6, который выглядит вот так:

Такой способ избавляет от необходимости сначала создавать массив, а потом присоединять все его элементы в строку. И ещё, так лучше читается. Но старый способ очень распространён в интернете, поэтому я решил показать оба.

Отлично! Двигаемся дальше!

Шаг №2

Теперь мы начинаем проверять, соответствует ли унарная версия нашего числа регулярному выражению. Это выражение можно разбить на две части, которые разделены символом | (который работает как оператор OR).

Левая часть выглядит так:

Давайте пройдёмся по каждому символу:

Первый символ: ^.

Он указывает регулярному выражению, что необходимо начинать проверку с начала строки. Таким образом, поиск паттернов начнётся с начала, а не с середины, конца или где бы то ни было ещё. Это противоположность символа $ , который указывает нашему выражению, где должен быть конец строки. Другими словами, вся строка целиком должна соответствовать выражению и не должно быть остатка.

Следом идёт: 1.

Здесь единица указывает, что в строке необходимо искать символ «1». Мы могли бы создать нашу «унарную строку» из двоек (т.е. 3 станет «222» и т.д.), тогда вместо 1 мы бы написали 2. Другими словами, этот символ должен совпадать с тем, что вы указывали, создавая строку.

Далее символ: ?.

Он указывает на то, что предыдущий символ необязателен, таким образом выражение сверит отсутствие “1” или одну «1» (“ ” или “1”).

Последний символ: $.

Как я уже говорил — это противоположность символа ^. Так мы узнаём, что в конце нет остатка.

Итак, эта часть регулярного выражения завершает шаг №2 — проверку, было ли число 0 или 1.

Отлично! Далее!

Шаг №3

Здесь начинается самое интересное. Нам нужно проверить, кратно ли число чему-то большему, чем единица. Если да, то оно не является простым числом. Давайте рассмотрим правую часть выражения:

Здесь у нас такой же паттерн ^...$ , указывающий места начала и конца проверки строки. Сперва давайте посмотрим, что происходит в скобках.

(11+?)

Скобки здесь нужны для группировки, это важно, потому что мы проверяем кратность. Если мы хотим убедиться, что наше число не кратно двум, нам нужно сгруппировать все единицы в виде «11…» и узнать есть ли остаток.

Первые две единицы внутри скобок, являются тем же что и 1 из предыдущей части. Они приводят наше число в соответствие с унарной версией строки.

Символ + указывает на необходимость соответствия одному или нескольким символам, предшествующим ему. Таким образом, необходимо как минимум две “1” для сопоставления. При этом любое количество “1”, большее чем это, тоже подойдёт.

Символ ? — очень важен. Он делает + менее «жадным». Т.е. сначала, выражение будет проверять наименьшую из возможных частей строки. Проверка начнётся с двух “1”, далее три “1”, потом четыре и т.д. Без символа ? выражение будет проверять строку столько, сколько это возможно, в нашем случае это вся строка, так как наша строка содержит только один символ.

Теперь у нас есть группа из двух или более “1”. Нам нужно проверить кратность и остаток во всей строке. За это отвечает \1+? .

Первая часть \1 называется обратная ссылка. Она ссылается на то, что было в первой группе нашего выражения между скобок. Представьте, что это своеобразная переменная в выражении.

Следом идёт +? , этот символ, должен быть вам знаком. Это «не жадная» проверка.

И так, если (11+?) совпадает со строкой “11”, значит наша обратная ссылка тоже будет соответствовать “11”. Наше регулярное выражение ищет всё что кратно “11”, начиная с “1111”, далее “111111” и т.д. Если наше число нечётное, поиск завершится неудачей, тогда добавляется ещё одна “1” внутрь скобок и проверка на кратность, теперь уже “111”, повторяется.

Если выражение возвратит true после проверки, значит наше число: а) 0 или 1, или б) кратно числу большему чем 1. То есть оно не является простым (!)! Здорово, правда?

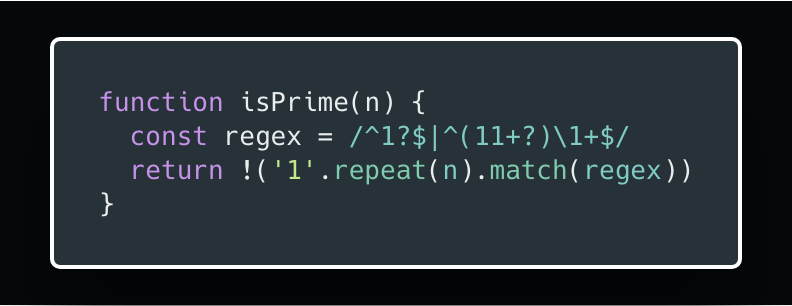
Посмотрите ещё раз этот код, чтобы проверить всё ли вы поняли:

Ещё есть версия с красивым синтаксисом ES6, которая позволяет избежать создания необязательного массива:

Пока это всё что я хотел показать. Спасибо за внимание. Надеюсь, вам было интересно, и вы готовы создавать собственные регулярные выражения.