SIMD в разработке игр

Часто при разработке игр мы говорим о SIMD. Это святой Грааль производительности процессора, часто недосягаемый. Принято считать, что реальных выгод от SIMD добиться трудно.

В надежде получить некоторый прирост производительности соблазнительно создать математическую библиотеку на основе SIMD. Однако зачастую доказанной выгоды в этом нет. Использовать приятно что-то, что, как нам известно, может повысить производительность. А SIMD иногда может даже помешать.

Например, разработчики игр часто выполняют множество фрагментарных векторных вычислений, но не шинкуют 8 морковок одновременно. Вместо этого они пытаются заставить работать на игрока саму способность перемещаться. Это как раскачиваться на веревке или плавать в воде. Требуется векторная математика, но такой код невозможно осмысленно собрать в инструкции SIMD. В игре нельзя заставить 8 игроков раскачиваться на веревке одновременно.

Физика игр часто схожа. Пользователь хочет создать или уничтожить одно тело. Лучи выдаются игрой по отдельности и направлены в разные стороны.

Даже если там вычисляется много похожего, собрать эти объекты и одновременно пропустить их через какой-нибудь алгоритм может быть сложно. Например, одно из самых дорогостоящих вычислений в игровой физике — вычисление сил контакта сталкивающихся тел. Когда их много, точек контакта может быть огромное количество.

Эта большая пирамида имеет 5050 тел и целых 14950 пар контактов, каждая из которых имеет две точки контакта. Каждая точка контакта имеет силу сопротивления и силу трения. То есть надо рассчитать 59800 сил! Кроме того, эти силы необходимо вычислять несколько раз за временной шаг в рамках решателя Soft Step. Подробности читайте здесь.

Пирамида из 5050 тел

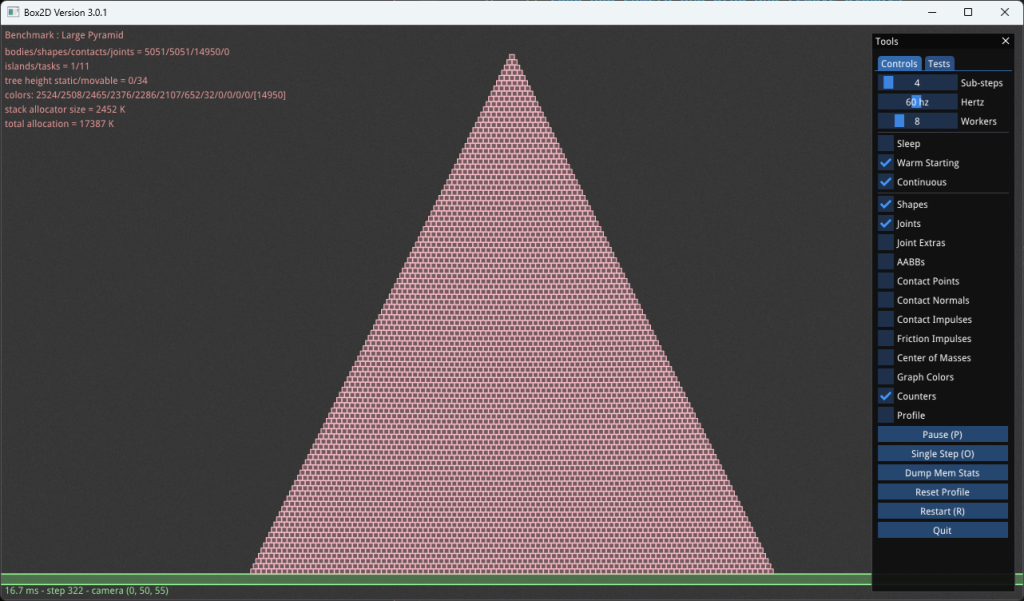
Другая проблема заключается в том, что каждое ограничение действует на разные тела. Таким образом, даже если для ускореенной итерации ограничения в массиве организованы последовательно, к телам должен быть произвольный доступ. В конечном счете этот произвольный доступ является узким местом игровой физики.

Раскраска графа

Для Box2D версии 3.0 я решил попробовать использовать SIMD, поскольку этот принцип вычислений предназначен для решения [задач] контактов. Ускорение решений этих задач может значительно поднять производительность, поэтому я решил, что затраченные усилия того стоят.

Но как мне собрать 4 или 8 пар контактов для одновременного решения? Ключевой момент — раскраска графа. Идея состоит в том, чтобы всем контактным ограничениям присвоить несколько цветов. Например, предположим, что у меня есть 6 цветов, и я хочу назначить всем контактам один из них. Контактные ограничения действуют на два тела одновременно. Ограничение раскраски графов состоит в том, что в пределах одного цвета тело может появляться только один раз или не появляться вообще.

Эта небольшая пирамида показывает пример раскраски графа. Каждое контактное ограничение имеет две контактные точки одного цвета. Есть четыре цвета: красный, оранжевый, желтый и зеленый. Если вы посмотрите на цвет, например оранжевый, то увидите, что для каждой пары точек контакта он касается поля только один раз. В этом и заключается магия раскраски графов, которая позволяет мне одновременно разрешить несколько контактных ограничений без состояния гонки.

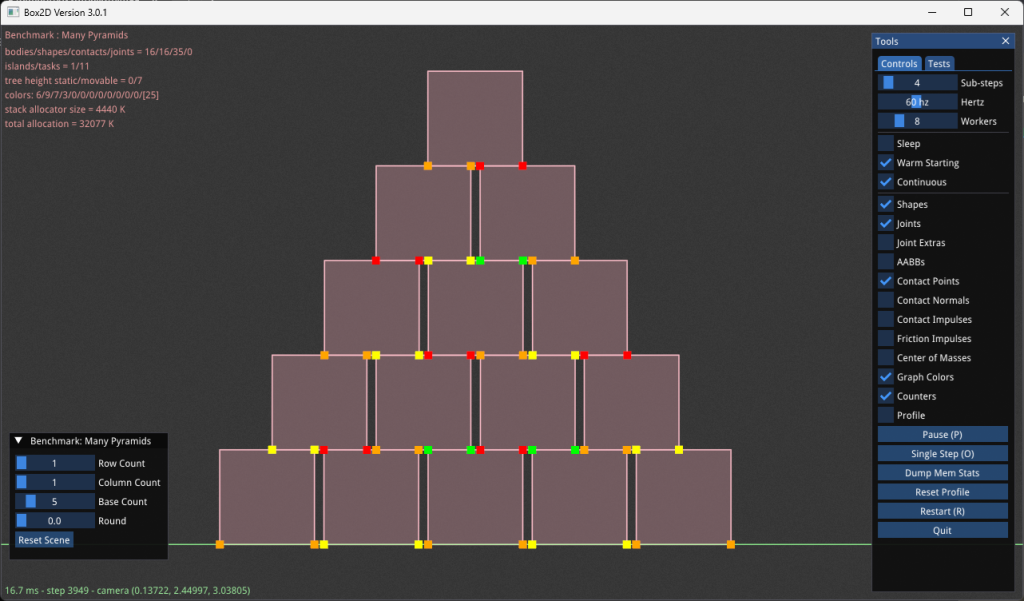
Раскраска графа маленькой пирамиды

Раскраска графов может быть очень большой задачей. На изображении ниже показана графическая раскраска точек контакта на большой пирамиде. Ниже вы увидите количество контактных ограничений для каждого цвета.

  • цвет 1 : 2524
  • цвет 2 : 2508
  • цвет 3 : 2465
  • цвет 4 : 2376
  • цвет 5 : 2286
  • цвет 6 : 2107
  • цвет 7 : 652
  • цвет 8 : 32
Раскраска большой пирамиды

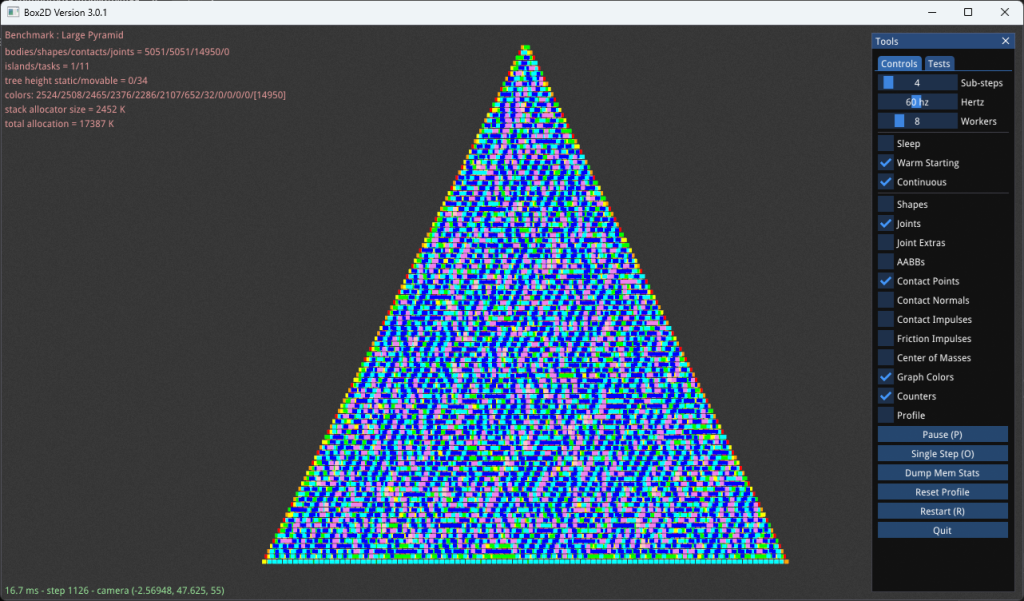
Эти цвета группируют ограничения, которые с помощью SIMD можно разрешить одновременно. Например, цвет 1 имеет 2524 ограничения. Каждое из этих ограничений находится между двумя телами. Раскраска графа гарантирует, что ни одно из одних и тех же тел не появится более одного раза во всех 2524 контактных ограничениях. Это означает, что все 2524 ограничения можно решить одновременно.

Но не является ли раскраска графов очень сложной и медленной? В моделировании твердого тела контакты постоянно возникают и исчезают. Нужно ли пересчитывать цвета графа каждый раз, когда контакт добавляется или удаляется?

Прежде всего, относительно раскраски графов есть много устрашающей теории, и на первый взгляд кажется, что для правильной раскраски графов необходимо применять некоторые сложные алгоритмы. Это совсем не так! Для игровой физики достаточно простого жадного алгоритма.

Box2D поддерживает битовые маски для каждого цвета графа. Каждый бит соответствует индексу тела. При создании контактного ограничения проверяются биты цвета графа. Ограничение назначается первому цвету с битовой маской, где ни один из битов тела не установлен в 1. Как только ограничение назначается цвету, эти два бита тела устанавливаются в 1. Эта операция очень быстрая.

void b2AddContactToGraph(b2ConstraintGraph* graph, b2Contact* contact)
{
    int indexA = contact->bodyIndexA;
    int indexB = contact->bodyIndexB;

    for (int i = 0; i < graph->colorCount; ++i)
    {
        b2GraphColor* color = graph->color + i;
        if (b2GetBit(color->bodySet, indexA))
        {
            // переход к следующему цвету
            continue;
        }

        if (b2GetBit(color->bodySet, indexB))
        {
            // переход к следующему цвету
            continue;
        }

        // найден доступный цвет!
        b2SetBit(color->bodySet, indexA);
        b2SetBit(color->bodySet, indexB);

        contact->colorIndex = i;
    }
}

Несмотря на то, что битовые маски работают быстро, лучше было бы не перекрашивать граф на каждом временном шаге. Таким образом, Box2D сохраняет окраску графа на разных отрезках шагах времени. Цвет определяется при создании контактного ограничения и включаются биты тела. Когда ограничение снимается, соответствующие два бита тела очищаются.

void b2RemoveContactFromGraph(b2ConstraintGraph* graph, b2Contact* contact)
{
    b2GraphColor* color = graph->color + contact->colorIndex;
    b2ClearBit(color->bodySet, contact->bodyIndexA);
    b2ClearBit(color->bodySet, contact->bodyIndexB);
    contact->colorIndex = B2_NULL_INDEX;
}

Есть еще пара деталей. Когда тела засыпают, они удаляются из раскраски графа, а когда просыпаются, добавляются обратно в соответствии со связывающими их ограничениями. Кроме того, в битовых масках никогда не задаются статические тела, ведь они не изменяются решателем. Это уменьшает количество необходимых цветов.

Проход по графу с типом wide

Итак, теперь, когда у меня есть 2524 контактных ограничения, которые я могу решить одновременно, как мне это сделать? Не существует SIMD-модулей с типом wide в 2524 чисел с плавающей точкой. Поэтому я разбиваю их на 4 или 8 блоков ограничений (SSE2/Neon или AVX2). Эти wide-ограничения можно решить как одно скалярное ограничение, математика почти идентична.

Чтобы разрешить ограничения, нужна тонкая сборка. В частности, для каждого wide-ограничения нужно собрать 4 или 8 пар тел. Я собираю скорости тела и помещаю их в wide float (4 или 8 чисел с плавающей точкой).

// wide float
typedef b2FloatW __m128;

// wide-вектор
struct b2Vec2W
{
    b2FloatW X;
    b2FloatW Y;
};

// wide-тело
struct b2BodyW
{
    b2Vec2W linearVelocity;
    b2FloatW angularVelocity;
};

Я беру 4 или 8 тел и помещаю их скорости в одно wide-тело. Тогда wide-ограничение действует на wide-тела, и вся математика выглядит аналогично скалярной математике. Например, скалярное произведение с типом wide представляет собой всего лишь два умножения и одно сложение, при этом одновременно выполняется 4 или 8 скалярных произведений.

// скалярное произведение с wide
b2FloatW b2DotW(b2Vec2W a, b2Vec2W b)
{
    return b2AddW(b2MulW(a.X, b.X), b2MulW(a.Y, b.Y));
}

Именно для этого предназначен SIMD. Но наверняка предстоит проделать большую работу с настройкой, чтобы это стало возможным!

После разрешения wide-ограничения скорости wide-тела рассеиваются на отдельные скалярные тела. Эти операции сборки и разборки необходимы, чтобы все это работало. В каждом наборе инструкций SSE2/Neon/AVX2 есть специальные инструкции, которые помогают в этом. Ни одна из них не суперинтуитивна, но они хорошо документированы, их не так уж трудно настроить.

Имеет ли это значение?

Я проделал всю эту работу, чтобы включить обработку при помощи SIMD. Она помогла? У Box2D есть консольное приложение для бенчмарков. Оно поможет ответить на этот вопрос. Я реализовал наборы инструкций SIMD SSE2, Neon и AVX в контактном решателе Box2D. И еще написал эталонную скалярную реализацию. У меня есть 5 сценариев тестирования, которые по-разному напрягают Box2D. Результаты здесь.

Я запускал эти тесты на AMD 7950X (AVX2, SSE2, скалярная) и Apple M2 (Neon).

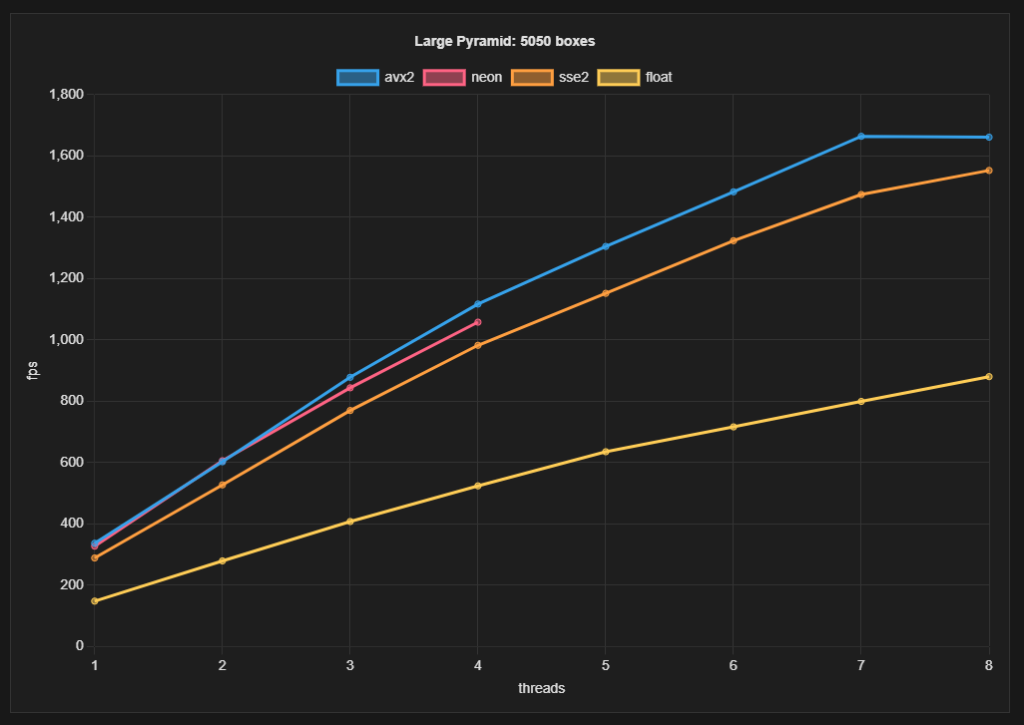
Результаты бенчмарка на большой пирамиде

Объединенная сетка визуализации вообще не показывает тест инструкций SIMD, поэтому его можно игнорировать. Но все остальные подчеркивают значения решателя контактов.

Бенчмарк большой пирамиды с 4 воркерами дает следующие цифры:

  • AVX2: 1117 fps = 0,90 мс;
  • Neon: 1058 fps = 0,95 мс;
  • SSE2: 982 fps = 1,02 мс;
  • скаляры (AMD): 524 fps = 1,91 мс;
  • скаляры (M2): 679 fps = 1,47 мс.

Из этого я делаю следующие выводы:

  1. SSE2 примерно в 2 раза быстрее скаляров.
  2. AVX2 примерно на 14% быстрее SSE2.
  3. Apple M2 курит в сторонке!

Еще одно соображение заключается в том, что все столкновения выполняются с помощью скалярной математики. Так что можно было бы получить больше, если бы я выяснил, как использовать SIMD и для коллизий.

Суть в том, что эффективное применение SIMD может потребовать много работы, но оно того стоит, поскольку позволяет играм работать значительно быстрее и обрабатывать более твердые тела.

А как насчет векторизации при компиляции?

Интересный побочный результат этого эксперимента связан с векторизацией компилятора. В моей эталонной скалярной реализации я определил wide-число с плавающей точкой как структуру из 4 чисел с плавающей точкой.

// wide-число с плавающей точкой для эталонной скалярной реализации
struct b2FloatW { float x, y, z, w };

Я реализовал все математические функции типа wide, чтобы они работали со структурой. Кажется, я идеально расположил все данные, чтобы компилятор мог векторизовать автоматически. Но, похоже, на самом деле векторизации не происходит в степени, достаточной для конкуренции с моей реализацией SSE2, написанной вручную. Это слегка иронично, ведь на x64 вся математика — математика SIMD, просто неэффективная.

Ссылки

Bepu Physics также использует раскраску графов и SIMD. Хотя я уже давно знал об этой технике, меня вдохновила высокая производительность Bepu.

Моделирование физики с высокой производительностью на архитектуре следующего поколения с большим количеством ядер. Это самая первая известная мне ссылка, где раскраску графов предлагается использовать, чтобы ускорить вычисления в физике твердого тела.

Раскраска графа используется во многих областях моделирования. Например, она очень полезна в моделировании ткани одежды. Преимущество такого моделирования заключается в том, что обычно раскраску графа можно вычислить предварительно.

Читайте также:

Читайте нас в Telegram, VK и Дзен

Перевод статьи Erin Catto: SIMD Matters

Предыдущая статьяКак Signal управляет состоянием приложения
Следующая статьяКомпоненты высшего порядка в React Virtualized