Тренды

Рост производительности машинного обучения с Rust

08.08.2023

Создадим с нуля небольшой фреймворк машинного обучения на Rust.

Цели

Выяснить, заметен ли рост скорости при переходе с Python и PyTorch на Rust и LibTorch, серверную библиотеку PyTorch на C++, особенно в процессе обучения модели. ML-модели становятся крупнее, для их обучения требуется больше вычислительных возможностей, для обычного человека порой нереальных. Один из способов уменьшить рост аппаратных требований — понять, как сделать алгоритмы вычислительно эффективнее. Python в PyTorch — это лишь слой поверх LibTorch. Вопрос в том, стоит ли менять его на Rust. Планировалось использовать крейт Tch-rs для доступа к тензорам и функционалу Autograd DLL-библиотеки LibTorch как «калькулятору градиентов», а затем разработать с нуля на Rust остальное.
Сделать код достаточно простым для четкого понимания всех вычислений линейной алгебры и с возможностью легко его расширить при необходимости.
Во фреймворке ML-модели должны определяться, насколько это возможно, по аналогичной структуре стандартных Python/PyTorch.
Поизучать Rust и не скучать.

Но статья посвящена скорее преимуществам применения Rust в машинном обучении.

Переходим сразу к конечному результату — вот как маленьким фреймворком создаются нейросетевые модели.

Листинг 1. Определение нейросетевой модели

struct MyModel {
    l1: Linear,
    l2: Linear,
}

impl MyModel {
    fn new (mem: &mut Memory) -> MyModel {
        let l1 = Linear::new(mem, 784, 128);
        let l2 = Linear::new(mem, 128, 10);
        Self {
            l1: l1,
            l2: l2,
        }
    }
}

impl Compute for MyModel {
    fn forward (&self,  mem: &Memory, input: &Tensor) -> Tensor {
        let mut o = self.l1.forward(mem, input);
        o = o.relu();
        o = self.l2.forward(mem, &o);
        o
    }
}

Затем модель инстанцируется и обучается.

Листинг 2. Инстанцирование и обучение нейросетевой модели

fn main() {
    let (x, y) = load_mnist();

    let mut m = Memory::new();
    let mymodel = MyModel::new(&mut m);
    train(&mut m, &x, &y, &mymodel, 100, 128, cross_entropy, 0.3);
    let out = mymodel.forward(&m, &x);
    println!("Training Accuracy: {}", accuracy(&y, &out));
}

Для пользователей PyTorch это интуитивно понятная аналогия определения и обучения нейросети на Python. В примере выше показана модель нейросети, используемая затем для классификации. Модель применяется к набору данных Mnist тестов производительности для сравнения двух версий модели: Rust и Python.

В первом блоке кода создается структура MyModel с двумя слоями типа Linear.

Второй блок — ее реализация, где определяется ассоциированная функция new, которой инициализируются два слоя и возвращается новый экземпляр структуры.

В третьем блоке реализуется типаж Compute для MyModel, им определяется метод forward. Затем в функции main загружается набор данных Mnist, инициализируется память, инстанцируется MyModel, а после она обучается в течение 100 эпох с размером пакета 128, потерями перекрестной энтропии и скоростью обучения 0,3.

Очень даже понятно: это то, что потребуется для создания и обучения новых моделей на Rust с помощью маленького фреймворка. Теперь копнем поглубже и разберемся, как это все возможно.

Если вы привыкли создавать ML-модели в PyTorch, то наверняка, глядя на код выше, зададитесь вопросом: «Зачем здесь ссылка на Memory?». Объясним ниже.

Прямой проход

Теоретически механизм обучения нейросети — это итеративное прохождение двух этапов в несколько эпох, нередко и пакетов, прямого прохода, а также обратного прохода, то есть обратного распространения.

При прямом проходе входные данные и последующие вычисления продвигаются по всем слоям сети, где для каждого слоя имеется:

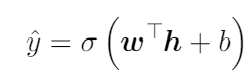
Линейная функция и функция активации на каждом уровне нейросети *(Goodfellow et. al., 2016)*

Здесь w — это веса для линейной функции, b — смещения. Затем она передается через функцию активации, например сигмоиду, которой обеспечивается нелинейность.

Теперь создадим слой Linear, см. листинг 3 ниже. Структуры для определения слоя и модели из листинга 1 аналогичны: в них реализуются те же функции и типажи.

В структуре слоя Linear имеется поле params. Это коллекция типа HashMap, в типе ключа которого String хранится имя параметра, а в типе значения usize содержится местоположение конкретного параметра, то есть тензора PyTorch, в Memory, где, в свою очередь, хранятся все параметры.

Листинг 3. Определение слоя «Linear» нейросети

trait Compute {
    fn forward (&self,  mem: &Memory, input: &Tensor) -> Tensor;
}

struct Linear {
    params: HashMap<String, usize>,
}

impl Linear {
    fn new (mem: &mut Memory, ninputs: i64, noutputs: i64) -> Self {
        let mut p = HashMap::new();
        p.insert("W".to_string(), mem.new_push(&[ninputs,noutputs], true));
        p.insert("b".to_string(), mem.new_push(&[1, noutputs], true));

        Self {
            params: p,
        }
    } 
}

impl Compute for Linear {
    fn forward (&self,  mem: &Memory, input: &Tensor) -> Tensor {
        let w = mem.get(self.params.get(&"W".to_string()).unwrap());
        let b = mem.get(self.params.get(&"b".to_string()).unwrap());
        input.matmul(w) + b
    }
}

Согласно уравнению 1, в ассоциированной функции new мы вставляем в HashMap два необходимых слою Linear параметра: W и b.

В представленном здесь же методе mem.new_push() создаются соответственные им тензоры требуемых размеров, помещаются в хранилище памяти, а возвращается их местоположение. Булевым параметром в методе insert определяется, что для этих параметров нужно вычислить градиент. Так, в каждом слое будут имена параметров и соответственные местоположения хранилища тензоров в структуре Memory.

Аналогично определению MyModel затем реализуется типаж Compute для слоя Linear. Для этого определяется функция forward, вызываемая во время прямого прохода процесса обучения.

В этой функции сначала с помощью метода get получаем ссылку на два тензорных параметра из хранилища тензоров, затем согласно уравнению 1 вычисляем линейную функцию. Как и в PyTorch, из нейросети выводим ненормализованные прогнозы, то есть логиты, затем при вычислении ошибки выполняем нормализацию Softmax.

Не проще ли прямо захардкодить уравнение 1 в одной-двух строках кода?

Но этот подход применяется так, что для определения типов дополнительного слоя, например, сверточной нейросети или нейросети долгой краткосрочной памяти нужно лишь точно скопировать структуру слоя Linear и ввести дополнительные параметры и вычисления в ассоциированной функции new и методе forward, и он сразу включится в модели согласно листингу 1.

При этом все тензоры размещаются в центральном хранилище, что удобно на этапе обратного распространения.

Вычисление ошибки

В конце прямого прохода вычисляется ошибка между прогнозными и целевыми значениями.

Ниже приведен код для вычисления среднеквадратичной ошибки, применяемого обычно для регрессии, и потери перекрестной энтропии — для классификации.

Листинг 4. Функции среднеквадратичной ошибки и потерь перекрестной энтропии

fn mse(target: &Tensor, pred: &Tensor) -> Tensor {
    (target - pred).square().mean(Kind::Float)
}

fn cross_entropy (target: &Tensor, pred: &Tensor) -> Tensor {
    let loss = pred.log_softmax(-1, Kind::Float).nll_loss(target);
    loss
}

И на этом прямой проход завершается, начинается обратный.

Обратный проход

При обратном проходе параметры модели обновляются с помощью градиентов, каждый из которых — это производная функции потерь по каждому соответственному параметру. На первом этапе получаем градиенты:

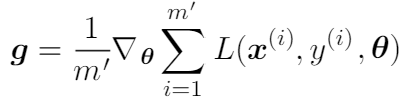
Уравнение 2. Производная функции потерь по параметрам модели *(Goodfellow et. al., 2016)*

Здесь m′ — это размер мини-пакета. Для каждого мини-пакета параметры обновляются так:

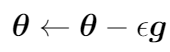
Уравнение 3. Правило обновления параметров с помощью градиента (Goodfellow et. al., 2016)

Здесь ε — это скорость обучения.

Чтобы получить градиенты, используем функционал Autograd из LibTorch. В PyTorch, чтобы вычислить производные, с потерями обычно задействуется метод backward, затем для применения градиентов к параметрам модели вызывается функция step из оптимизатора. Здесь процесс тот же, но для применения градиентов функция step не задействуется напрямую. Ведь мы не расширяем модели из класса nn.Module и не используем оптимизаторы PyTorch, как это обычно происходит в Python. Поэтому о части со step позаботимся отдельно.

Во фрагменте кода ниже, в листинге 5, показана реализация тензора в Memory, а также функционал step для градиентов. Хранилище тензоров представлено структурой с двумя полями: size — количество хранимых в данный момент тензоров и values — вектор тензоров. В блоке реализации метод new занят инициализацией хранилища, методы push, new_push, get — передачей назад-вперед тензоров, последние два использованы в слое Linear выше.

Листинг 5. Хранилище тензоров «Memory»

struct Memory {
    size: usize,
    values: Vec<Tensor>,
}

impl Memory {

    fn new() -> Self {
        let v = Vec::new();
        Self {size: 0,
            values: v}
    }

    fn push (&mut self, value: Tensor) -> usize {
        self.values.push(value);
        self.size += 1;
        self.size-1
    }

    fn new_push (&mut self, size: &[i64], requires_grad: bool) -> usize {
        let t = Tensor::randn(size, (Kind::Float, Device::Cpu)).requires_grad_(requires_grad);
        self.push(t)
    }

    fn get (&self, addr: &usize) -> &Tensor {
        &self.values[*addr]
    }

    fn apply_grads_sgd(&mut self, learning_rate: f32) {
        let mut g = Tensor::new();      
        self.values
        .iter_mut()
        .for_each(|t| {
            if t.requires_grad() {
                g = t.grad();
                t.set_data(&(t.data() - learning_rate*&g));
                t.zero_grad();
            }
        });
    }

    fn apply_grads_sgd_momentum(&mut self, learning_rate: f32) {
        let mut g: Tensor = Tensor::new();
        let mut velocity: Vec<Tensor>= Tensor::zeros(&[self.size as i64], (Kind::Float, Device::Cpu)).split(1, 0);
        let mut vcounter = 0;
        const BETA:f32 = 0.9;
        
        self.values
        .iter_mut()
        .for_each(|t| {
            if t.requires_grad() {
                g = t.grad();
                velocity[vcounter] = BETA * &velocity[vcounter] + (1.0 - BETA) * &g;
                t.set_data(&(t.data() - learning_rate * &velocity[vcounter]));
                t.zero_grad();
            }
            vcounter += 1;
        });
    }
}

Последними двумя методами в этом коде реализуются алгоритмы базового градиентного спуска и градиентного спуска с импульсом. Предполагается, что функция step с backward для генерирования градиентов уже вызвана, поэтому здесь у нас то, что в PyTorch было бы вызовом функции step.

В процессе выполняется проход циклом каждого тензора хранилища, методом grad получается вычисленный градиент, затем вызовом метода set_data применяется правило обновления параметров. Здесь легко добавить другие методы, реализовать другие алгоритмы, такие как Rmsprop и Adam.

Цикл обучения

В цикле обучения объединяем все рассмотренное выше для процесса обучения. Как обычно, проходимся циклом по каждой эпохе, в которой затем так же проходимся по каждому мини-пакету и для каждого мини-пакета выполняем прямой проход, вычисляем ошибку, для генерирования градиентов вызываем на ней метод backward, затем применяем градиенты.

Листинг 6. Цикл обучения

fn train<F>(mem: &mut Memory, x: &Tensor, y: &Tensor, model: &dyn Compute, epochs: i64, batch_size: i64, errfunc: F, learning_rate: f32) 
    where F: Fn(&Tensor, &Tensor)-> Tensor    
        {
        let mut error = Tensor::from(0.0);
        let mut batch_error = Tensor::from(0.0);
        let mut pred = Tensor::from(0.0);
        for epoch in 0..epochs {
            batch_error = Tensor::from(0.0);
            for (batchx, batchy) in get_batches(&x, &y, batch_size, true) {
                pred = model.forward(mem, &batchx);
                error = errfunc(&batchy, &pred);
                batch_error += error.detach();
                error.backward();
                mem.apply_grads_sgd_momentum(learning_rate);              
            }
            println!("Epoch: {:?} Error: {:?}", epoch, batch_error/batch_size);
        }
}

Хотя в PyTorch имеются классы Dataset и Dataloader для мини-пакетной обработки данных, мы создали свой механизм такой обработки.

В листинге 7 функцией на Rust принимается ссылка на полный набор данных, и, чтобы перебрать мини-пакеты с помощью функции обучения из листинга 6, возвращается итератор.

Листинг 7. Мини-пакетная обработка

fn get_batches(x: &Tensor, y: &Tensor, batch_size: i64, shuffle: bool) -> impl Iterator<Item = (Tensor, Tensor)> {
    let num_rows = x.size()[0];
    let num_batches = (num_rows + batch_size - 1) / batch_size;
    
    let indices = if shuffle {
        Tensor::randperm(num_rows as i64, (Kind::Int64, Device::Cpu))
    } else 
    {
        let rng = (0..num_rows).collect::<Vec<i64>>();
        Tensor::from_slice(&rng)
    };
    let x = x.index_select(0, &indices);
    let y = y.index_select(0, &indices);
    
    (0..num_batches).map(move |i| {
        let start = i * batch_size;
        let end = (start + batch_size).min(num_rows);
        let batchx: Tensor = x.narrow(0, start, end - start);
        let batchy: Tensor = y.narrow(0, start, end - start);
        (batchx, batchy)
    })
}

Финальные, вспомогательные функции

Последние две функции для запуска полного кода — вспомогательные, см. листинг 8.

Первой функцией загружается набор данных из каталога data, но прежде загружаем набор данных Mnist.

Второй функцией вычисляется точность модели, в качестве параметров принимается ссылка на целевое и прогнозные значения.

Листинг 8. Последние две вспомогательные функции

fn load_mnist() -> (Tensor, Tensor) {
    let m = vision::mnist::load_dir("data").unwrap();
    let x = m.train_images;
    let y = m.train_labels;
    (x, y)
}

fn accuracy(target: &Tensor, pred: &Tensor) -> f64 {
    let yhat = pred.argmax(1,true).squeeze();
    let eq = target.eq_tensor(&yhat);
    let accuracy: f64 = (eq.sum(Kind::Int64) / target.size()[0]).double_value(&[]).into();
    accuracy
}

Импортируем только это:

Листинг 9. Необходимый импорт

use std::{collections::HashMap};
use tch::{Tensor, Kind, Device, vision, Scalar};

Прежде чем запускать код, с сайта PyTorch загружаем LibTorch, библиотеку C++.

Результаты и мнения

Объективность сравнения рассмотренного кода с его эквивалентом на Python и PyTorch обеспечивается главным образом применением одинаковых гиперпараметров нейросети, алгоритмов и параметров обучения.

Для тестов применялся набор данных Mnist с 60 000 примеров обучения и признаками 28 x 28. Тесты запускались на ноутбуке Surface Pro 8, i7 с 16 Гб оперативной памяти, без графического процессора. В ходе многократных прогонов обучение на Rust выполнялось в среднем в 5,5 раза быстрее, чем на Python.

Пока не выявлено, где в процессе обучения достигнут наибольший рост производительности по сравнению со стандартным подходом PyTorch: в циклах обучения, в вычислении ошибки, в функционале step для градиентов и т. д. Поэтому имеется в виду общий рост относительно всего процесса.

На разработку всего этого на Rust с нуля требуется больше времени, особенно новичкам. Но стоит сделать все библиотечные компоненты и конвейерный код, чтобы оставалось только протестировать/создать новые модели, как в листинге 1, и тогда это станет, по моему мнению, не сложнее работы на Python.

Увеличение скорости обучения не следует игнорировать: так экономится много часов, если не дней, особенно в связи с усложнением ML-моделей, укрупнением наборов данных или огромными итеративными процессами обучения, как при обучении с подкреплением.

Использованные материалы

Ян Гудфеллоу, Йошуа Бенджио и Аарон Курвилль «Глубокое обучение», MIT Press, 2016 г.

Рост производительности машинного обучения с Rust

Цели

Листинг 1. Определение нейросетевой модели

Листинг 2. Инстанцирование и обучение нейросетевой модели

Прямой проход

Листинг 3. Определение слоя «Linear» нейросети

Вычисление ошибки

Листинг 4. Функции среднеквадратичной ошибки и потерь перекрестной энтропии

Обратный проход

Листинг 5. Хранилище тензоров «Memory»

Цикл обучения

Листинг 6. Цикл обучения

Листинг 7. Мини-пакетная обработка

Финальные, вспомогательные функции

Листинг 8. Последние две вспомогательные функции

Листинг 9. Необходимый импорт

Результаты и мнения

Использованные материалы

Читайте также

Основные принципы кэширования веб-приложений

Введение в байт-код Java

3 случая, когда линейная модель может ошибаться

Тесты

Насколько хорошо вы понимаете принципы работы ОС?

Какая из профессий в IT-сфере подойдет именно вам?

Насколько хорошо вы разбираетесь в Windows?