Предположим, вы ищете человека по имени “Эльвира” в огромном телефонном справочнике. Он может состоять из 100 страниц, и было бы утомительно изучать каждую из них с самого начала линейным способом, пока вы не найдете девушку с нужным вам именем. К счастью, имена в справочнике расположены в алфавитном порядке — это большой плюс.
Представьте, что вы открываете справочник на середине. Вы смотрите на страницу и видите имена, начинающиеся на “Н”. Зная, что буква “Э” идет после “Н”, вы разрываете справочник пополам и выбрасываете ту его половину, которая содержит имена до буквы “Н”. У вас в руках осталась книга меньшего размера.
Затем вы снова открываете справочник на середине. Теперь вы видите имена, начинающиеся на букву “С”. Вы снова разрываете справочник пополам и выбрасываете ту половину, которая содержит имена до “С”.
Продолжайте повторять эту процедуру, и вскоре вы окажетесь на страницах с буквой “Э”.
Мы только что описали концепцию бинарного поиска. Это эффективный алгоритм поиска значений в отсортированном массиве или списке.
Бинарный поиск является частью большой категории алгоритмов типа разделяй и властвуй. Эти классы алгоритмов берут сложную задачу и делят ее на мелкие подзадачи, которые легче решить. В бинарном поиске на каждом этапе задача делится пополам.
Чтобы проиллюстрировать работу этого алгоритма, предположим, что нужно найти 89 в следующем упорядоченном массиве чисел. Внизу и сверху на диаграмме находятся переменные, содержащие начальный и конечный индекс.
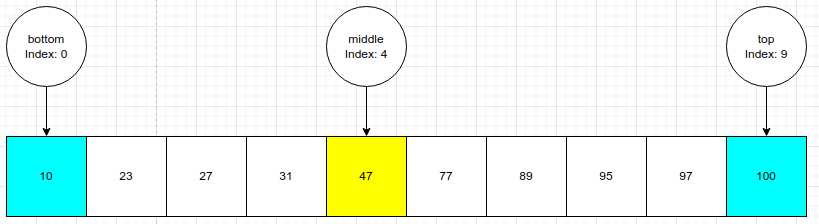
Начнем с вычисления среднего значения, используя нижнюю и верхнюю переменные. Среднее значение равно 47 — это не то значение, которое нам нужно. Поскольку мы знаем, что 47 < 89, мы можем исключить левую половину массива (все значения до 47 включительно). Это делается путем присвоения нижней переменной среднего индекса +1 (middle index +1). Размер задачи уменьшился вдвое.
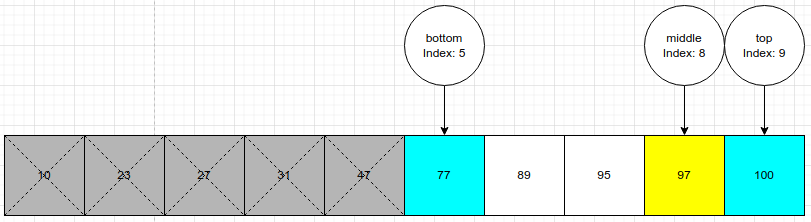
Процесс повторяется снова. Мы вычисляем, что среднее значение равно 97. Мы знаем, что 97 > 89, и правую половину массива можно исключить из поиска, присвоив верхней переменной средний индекс -1 (middle index -1).
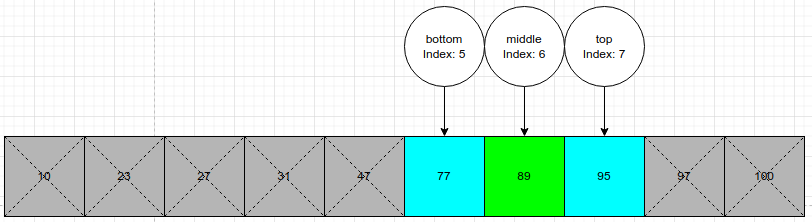
Повторяем процесс еще раз. Среднее значение вычисляется равным 89. Мы видим, что 89 = 89, и поэтому можем прекратить поиск и вернуть значение/индекс!
При линейном поиске пришлось бы выполнять 7 шагов, а бинарный поиск потребовал всего 3, чтобы найти число 89. Если работать с массивом небольшого размера, то разница во времени вычислений между двумя алгоритмами будет незначительной. Но при больших массивах данных с миллионами значений бинарный поиск окажется более эффективным, чем линейный.
Псевдокод
Этапы бинарного поиска можно описать следующим образом.
- Создание переменной bottom (нижней), указывающей на нижнюю границу подмассива.
- Создание переменной top (верхней), указывающей на верхнюю границу подмассива.
- Создание переменной middle (средней), указывающей на середину подмассива.
- Пока bottom остается <= top, нужно выполнить следующие действия.
- Вычислить среднее значение.
- Если среднее значение = целевому значению, вернуть индекс.
- Если значение середины < целевого значения, установить bottom = middle +1.
- Если среднее значение > целевого значения, установить top = middle -1.
5. Целевого значения нет в массиве.
Визуальная демонстрация
Это небольшое приложение наглядно демонстрирует идею бинарного поиска. Целевое значение — это число, которое нужно угадать, а догадки, которые делает пользователь, являются средним значением в алгоритме бинарного поиска.
Читайте также:
- Поиск с возвратом в решении типичных задач на собеседовании
- Алгоритмы поиска, которые должен знать каждый специалист по обработке и анализу данных
- 8 базовых алгоритмических задач на собеседованиях
Читайте нас в Telegram, VK и Дзен
Перевод статьи Xihai Luo: Introduction to Binary Search






