Как вычислить миллионное число Фибоначчи на Python

Как-то раз я захотел найти оптимальное решение для вычисления чисел Фибоначчи и решил попробовать вычислить стотысячное число в последовательности, а потом подумал: если бы я мог вычислить стотысячное, то почему бы не вычислить миллионное число? Поэтому сейчас я покажу, как у меня это получилось и с какими проблемами я столкнулся.

Последовательность Фибоначчи является одной из наиболее известных математических последовательностей и самым простым примером рекурсий. Каждое число последовательности состоит из суммы двух предыдущих, где начальными числами выступают 0 и 1. Выглядит это всё вот так:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 и так до бесконечности…

В течение следующих нескольких минут я пройдусь по нескольким различным подходам, а затем покажу оптимальное решение задачи:

1. Простая рекурсия.

2. Использование кэша с рекурсией.

3. Итеративный метод.

4. Использование формулы Бине.

5. Вычисление миллионного числа.

Перед тем как начать, нужно отметить, что все упомянутые замеры времени основаны именно на моем оборудовании и на версии Python 3.9.1.

1. Простая рекурсия

Это очень простой способ вычислить n-ное число Фибоначчи в Python:

def recursiveFib(n):
    if n == 1 or n == 2:
        return 1

    return recursiveFib(n - 1) + recursiveFib(n - 2)

Этот метод использует рекурсию, чтобы многократно вызывать функцию вычисления, рассчитывая предыдущее число и применяя его для вычисления следующего. Однако это и является недостатком метода, так как эта функция крайне неэффективная и ресурсоёмкая, ведь на каждой стадии она вычисляет два предыдущих числа, потом два предыдущих числа этого числа и так далее. В какой-то момент вы заметите, что вычисление одного числа будет занимать слишком много времени. На моем компьютере, например, вычисление 35-го числа Фибоначчи заняло 1,43 секунды. Поэтому очевидно, что вычисление еще больших значений стало бы невероятно медленным либо вообще практически невыполнимым.

2. Использование кэша с рекурсией

Поскольку мы постоянно вычисляем предыдущие два числа, то мы также можем использовать возможности кэширования для хранения числа, чтобы нам больше не нужно было их вычислять. Встроенный модуль functools позволяет нам использовать метод вытеснения из кэша (least recently used cache)  —  тип кэша, при котором все элементы в нем упорядочиваются по мере использования. Этот метод может значительно ускорить процесс.

from functools import lru_cache

@lru_cache()
def recursiveFibCached(n):
    if n == 1 or n == 2:
        return 1

    return recursiveFibCached(n - 1) + recursiveFibCached (n - 2)Первым делом, из модуля functools нужно импортировать декоратор lru_cache и поместить его перед функцией. Мы можем указать значение maxsize, чтобы обозначить, сколько элементов должно храниться в кэше, однако по умолчанию указывается 128, чего точно должно хватить. Благодаря использованию кэша мы можем вычислить 200-е число Фибоначчи всего за 0.0002252 секунды!

Однако единственной проблемой такой рекурсии является то, что если попытаться вычислить 501-е число, то программа выдаст ошибку RecursionError: maximum recursion depth exceeded in comparison. Эту проблему можно обойти, установив глубину рекурсии на какое-нибудь большее значение.

import sys

sys.setrecursionlimit(5000)

Теперь, чтобы вычислить тысячное число Фибоначчи, требуется лишь 0,001198 секунд. Однако с этим методом у меня случилась еще одна проблема, потому что по какой-то неведомой причине я так и не смог вычислить 1553-е число в последовательности, и даже после увеличения глубины рекурсии ничего не помогло: терминал переставал выдавать число и просто завершал работу программы. Это, очевидно, проблема и недостаток на пути к вычислению миллионного числа Фибоначчи.

3. Итеративный метод

Можно заметить, что в среде программистов использование рекурсивного метода решения проблемы часто рассматривается как плохая практика, гораздо лучше считаются итеративные методы вычисления. Мы также можем придумать итеративное решение для генерации чисел Фибоначчи:

def iterativeFib(n):
    a, b = 0, 1

    for i in range(n):
        a, b = b, a + b

    return a

Этот метод можно использовать для вычисления любого числа Фибоначчи (однако я не проверял его на огромных числах), что также происходит очень быстро, так как всего за 0.0028195 я смог вычислить десятитысячное число Фибоначчи. И если подумать, почему бы не использовать этот метод для вычисления миллионного числа: это возможно, однако займет какое-то время перед тем как полностью загрузиться. Читайте дальше, и я расскажу, почему так происходит.

4. Формула Бине

Формула Бине  —  это формула, которую можно использовать для вычисления n-ного числа последовательности Фибоначчи, а это как раз то, что нам нужно. Эта формула названа в честь французского математика Жака Филиппа Мари Бине. Вот как она выглядит:

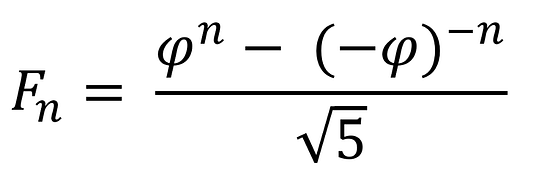
Фи (φ) равна золотому сечению:

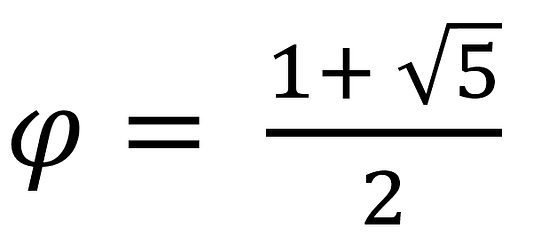
Эту формулу мы можем использовать, если перенести ее в Python:

def formulaFib(n):
    root_5 = 5 ** 0.5
    phi = ((1 + root_5) / 2)

    a = ((phi ** n) - ((-phi) ** -n)) / root_5

    return round(a)

Обратите внимание, что в реализации на Python нам следует вернуть округленную версию вычисленного числа, так как при вычислении больших чисел Python возвращает число, в котором после запятой может быть более двадцати девяток в периоде. И это хорошо, поскольку теперь у нас нет циклов и мы можем сразу вычислить ответ, ведь так? Но и в этом методе есть небольшой недостаток. Если мы попытаемся вычислить что-либо выше 1475-го числа, то столкнемся с ошибкой: OverflowError: (34, result too large). Это связано с тем, что в Python реализована система float, и она может иметь только определенное максимальное значение, которое мы превышаем, используя этот метод.

Эту проблему можно очень легко решить с помощью встроенного модуля Decimal, чтобы создать десятичный объект с гораздо большей точностью и размером для использования в нашем уравнении:

import decimal

def formulaFibWithDecimal(n):
    decimal.getcontext().prec = 10000

    root_5 = decimal.Decimal(5).sqrt()
    phi = ((1 + root_5) / 2)

    a = ((phi ** n) - ((-phi) ** -n)) / root_5

    return round(a)

В этой новой функции мы устанавливаем значение точности до 10000 цифр и преобразуем значение корня из 5 в десятичный объект, а затем используем его в нашем уравнении. Такой способ позволяет нам легко вычислить десятитысячное число последовательности за невероятные 0,0692986 секунд, что является огромным улучшением по сравнению со всеми предыдущими методами.

5. Вычисление миллионного числа

Как вы, возможно, заметили, применение формулы работает значительно медленнее итеративного метода, если n = 10000. Это связано с тем, что в формуле нам нужно создавать десятичный объект и использовать его в уравнении, а это занимает больше времени, чем повторение одного и того же действия 10000 раз. Однако это еще не конец истории.

Если увеличить количество повторений, необходимых для выполнения цикла, то это может значительно увеличить время завершения всего процесса. В какой-то момент, когда n достигает примерно 89200, время расчета при итеративном методе становится равным времени вычисления по формуле, а когда n увеличивается еще больше, то время итеративного метода увеличивается больше, чем по сравнению с увеличением времени по формуле.

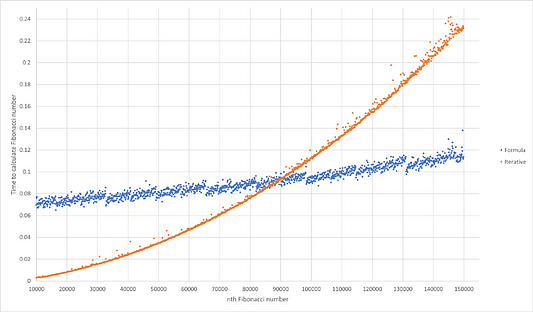
На графике видно, в какой точке пересекаются формула и итеративный метод. По мере увеличения n, время, затрачиваемое на расчет чисел Фибоначчи по формуле, растет в линейной прогрессии. А при итеративном решении время увеличивается вместе со значением n. Это дает нам понять, что миллионное число нужно будет вычислять по формуле. Кроме того, в качестве дополнительной меры для более точного вычисления числа мне пришлось поменять точность десятичного объекта с помощью decimal.getcontext().prec = 300000.

На моем компьютере (а у вас это время может быть другим) вычисление миллионного числа Фибоначчи заняло:

• 8,832661 секунд с применением итеративного метода
• 1,151380 секунд, используя формулу Бине, что в 7,7 раз быстрее!

Если вам хочется увидеть само число, оно состоит из 208988 цифр и в виде текстового файла весит 209 Кб:

Само число

Заключение

Вот так я и вычислил миллионное число Фибоначчи. Да, конечно, можно было вычислить число и побольше, но на самом деле это не имеет практического смысла, да и заняло бы много времени даже с применением формулы Бине. Из графика выше можно прикинуть, что на вычисление миллиардного числа Фибоначчи потребуется 310,8467 секунд. Оставлю эти расчёты на ваше усмотрение.

Читайте также:

• Топ-15 лайфхаков для работы с Python
• F-строки и 3 эффективных способа их применения
• Асинхронная многопоточность в Python

Читайте нас в Telegram, VK и Яндекс.Дзен

---

Перевод статьи Kush: How I calculated the 1,000,000th Fibonacci Number with Python