Графы в большинстве своем представляют собой неупорядоченные деревья. В основном это утверждение касается ненаправленных и невзвешенных графов. Однако оно остается в силе и в отношении направленных или взвешенных графов, либо направленных и взвешенных одновременно, только при этом надо детализировать понятие “неупорядоченности”.
Направленные графы
Прежде, чем познакомиться с направленным графом, взгляните на ненаправленный граф, представленный ниже:
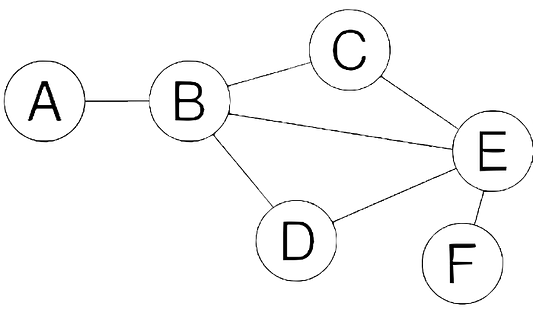
Ненаправленный граф позволяет свободно перемещаться между вершинами в любом направлении. Теперь посмотрите на направленную версию этого графа:
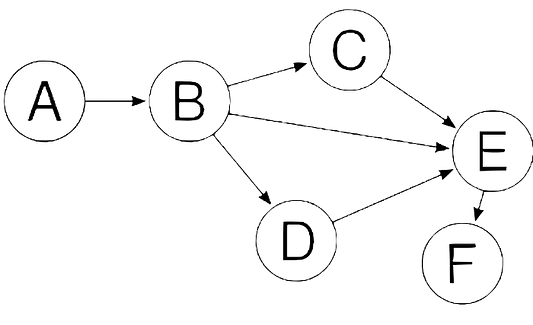
Тут все меняется. Вы можете перемещаться между вершинами только в направлении стрелки, прикрепленной к каждому ребру. Например, вы можете перейти из пункта А в пункт В, но не из пункта В в пункт А. Немного более строго, верно?
Взвешенные графы
Теперь подумаем о том, чтобы добавить веса ребрам графа. Представьте себе, что у каждого ребра есть цена; цена, которую нужно заплатить, чтобы пересечь ребро. Но перед этим представьте, что все ребра бесплатные, то есть имеют нулевую цену.
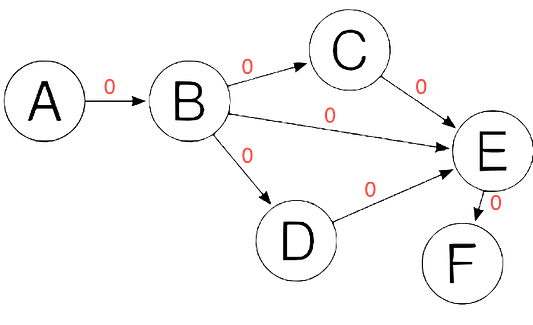
На самом деле это мало что меняет, так как с самого начала не было никакой цены, которую нужно было платить. Мы все еще можем пройти по графу без раздумий, если будем следовать указаниям стрелок. Даже если у каждого ребра есть цена, пока все они равны, поскольку каждое ребро имеет одинаковое значение, или вес.
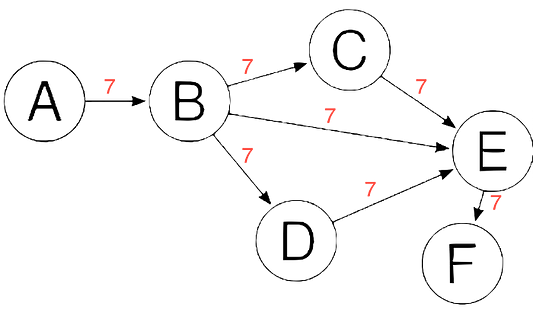
Хорошо, но что, если бы цены были другими? Как бы это изменило способ прохождения по графу?
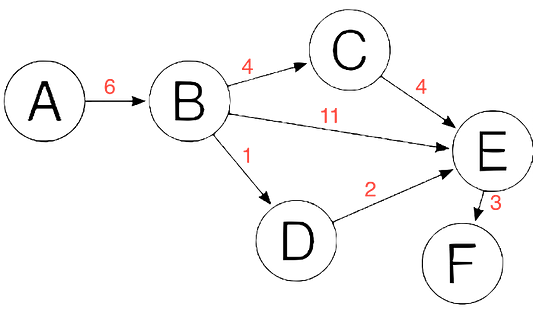
Поскольку цены теперь отличаются друг от друга, вводится новая динамика. Переход от вершины к вершине будет стоить разных сумм “денег”. Иногда есть только один путь, но в некоторых случаях можно выбрать маршрут, и цена обычно служит определяющим фактором в этом решении. В общем, при переходе из одной вершины графа в другую “самый дешевый” путь является желаемым. Например, если бы я хотел выбрать самый дешевый путь из пункта А в пункт Е, я бы пошел по маршруту АBDЕ. Хотя первоначальным решением мог бы стать маршрут ABE, на самом деле он вышел бы дороже. Подсчеты показывают: стоимость ABE составляет 11, в то время как АBDЕ — всего 9. Надеюсь, вы получили основное представление о взвешенных графах.
До этого момента я называл числа, представляющие каждое ребро, его “ценой”, имея в виду деньги. На самом деле эти цифры обозначают “вес” ребра. Аналогия с деньгами упрощает знакомство с этим видом графа, поскольку деньги — это то, с чем все мы знакомы. Есть и другие способы рассмотрения взвешенного графа. Вы можете представить числа как расстояние между двумя вершинами. Большинство иллюстраций графов не соотнеслись бы с таким представлением, но, тем не менее, такая аналогия тоже приемлема.
Представление графов в коде
Итак, вы уже знаете, что такое направленные и взвешенные графы. Теперь выясним, как представить графы в коде. До сих пор мы использовали только иллюстрации графов. Что ж, оказывается, существует множество способов их представления в коде. Рассмотрим некоторые из них в отношении направленного и невзвешенного графа, показанного ранее.
Список ребер
Список ребер — это именно то, на что похож приведенный ниже код; это список всех ребер на графе. Обратите внимание: каждое ребро представлено своими вершинами — начальной и конечной.
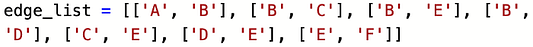
Список смежности
Список смежности — это что-то вроде словаря, в котором каждый ключ является вершиной в графе, а каждое значение — это все, к чему эта вершина примыкает. В направленном графе стрелки должны быть направлены так, чтобы вершина была ключом в списке.

Матрица смежности
Чтобы лучше понять матрицу смежности, изобразим ее в виде рисунка. Если у вас есть опыт работы с матрицами в исчислении, то вам это дастся довольно легко. Если нет, не стоит беспокоиться — всему свое время.
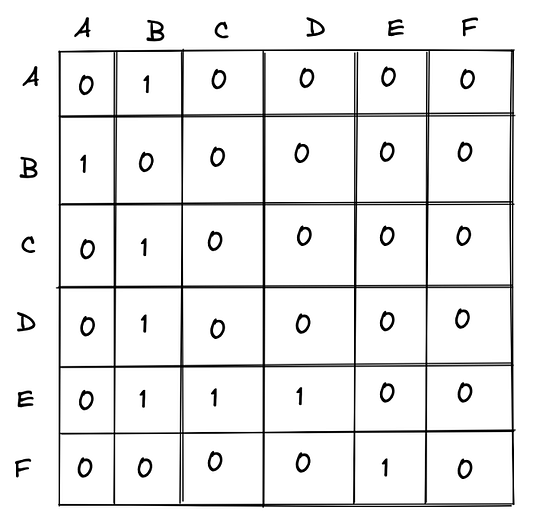
В матрице смежности “0” означает, что две вершины не являются смежными, а “1”, указывает на то, что они являются смежными. Существует множество способов манипулировать такой матрицей и работать с ней, но это выходит за рамки данного объяснения. Обратите внимание на то, что на диагонали есть только нули. Подумайте, почему это так…
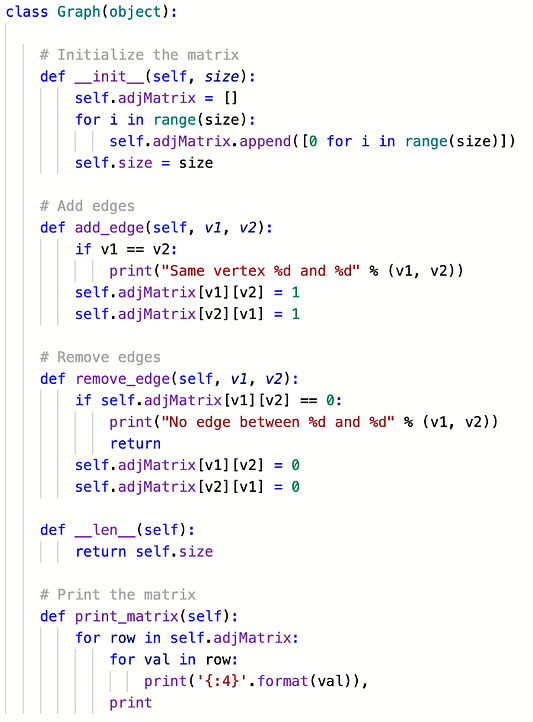
Для кодирования матрицы смежности существует несколько способов. В следующих случаях используется ООП:
Когда следует использовать каждый метод
Каждый метод является допустимым представлением графа. Когда же предпочесть один из них всем остальным? Если коротко, то это зависит от того, что вы делаете и как собираетесь манипулировать данными. Например, матрица смежности великолепна и проста в использовании, но может занимать гораздо больше памяти, чем, скажем, список ребер. Обратите внимание и на то, что каждый метод годится для указания веса ребра в случае со взвешенным графом; эта информация была исключена из примеров для упрощения.
Заключение
Мир графов в компьютерных науках огромен. Возможно, для вас это было первое знакомство с ним. Надеемся, что теперь вы лучше сможете понять основы продвижения проектов.
Для дальнейшего погружения в тему рекомендуем изучить алгоритмы обхода, такие как DFS (поиск в глубину) и BFS (поиск в ширину).
BFS, geeksforgeeks.org
DFS, geeksforgeeks.org
Читайте также:
- Создайте приложение для резюмирования новостных статей с Hugging Face и Gradio
- Погружение в базы данных
- Отслеживание фокусированного времени с помощью Python
Читайте нас в Telegram, VK и Яндекс.Дзен
Перевод статьи Jaylen Schelb, A Deeper Dive Into Graphs






