Вы можете использовать IRM практически в любой базовой модельной структуре. Однако эта система наиболее эффективна, когда ее применяют к моделям черного ящика, оперирующим большим количеством данных (нейронные сети и их многочисленные разновидности).
Давайте же узнаем, как это работает.
1. Техническая справка
В общих чертах IRM представляет собой парадигму обучения, направленную на исследование не корреляционных, а причинно-следственных связей. Разрабатывая обучающие среды и структурированные выборки данных, мы можем достичь максимальной точности и гарантировать при этом инвариантность предикторов. Те предикторы, которые подходят под наши данные и отличаются инвариантностью в разных средах, используются в качестве выходных данных в окончательной модели.
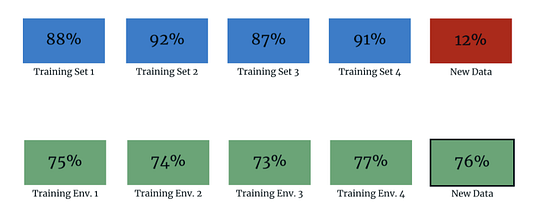
Шаг 1. Разрабатываем наборы сред. Вместо того, чтобы перетасовывать данные и предполагать, что они являются IID (независимыми и случайно распределенными), мы используем знания о нашем процессе отбора данных для разработки сред выборки. Например, для модели, которая анализирует текст на изображении, сгруппировать учебные среды может человек, который написал этот текст.
Шаг 2. Сводим к минимуму потери в разных средах. После разработки сред мы подбираем предикторы, которые примерно являются инвариантными, и оптимизируем точность в разных средах. Дополнительную информацию см. в пункте 2.1.
Шаг 3. Получаем лучший уровень обобщения! Методы инвариантной минимизации рисков демонстрируют более высокую точность относительно данных, находящихся вне распределения, чем традиционные парадигмы обучения.
2. Принцип работы
Давайте подробнее остановимся на том, как работает инвариантная минимизация рисков.
1.1 Какова цель создания прогностических моделей?
Изначальная цель прогностической модели состоит в том, чтобы обобщить скрытые данные т.е. достичь хороших результатов при работе с ними. Мы называем скрытые данные данными вне распределения (OOD).
Для моделирования новых данных внедряются различные методы, например, перекрестная проверка. Хотя этот способ эффективнее, чем оперирование простым обучающим набором, наши возможности в этом случае все еще ограничены объемом наблюдаемых данных. Можете ли вы быть уверены, что такая модель будет обобщать? Как правило, нет.
Если перед вами стоит четко определенная задача и при этом вы очень хорошо понимаете механизм генерации данных, вы можете быть уверены в том, что ваша выборка данных отражает реальную картину. Однако в большинстве случаев нам не хватает понимания этого механизма.
Возьмем пример, приведенный в работе, на которую мы ссылались выше. Мы хотим решить интригующую задачу по определению того, какое животное изображено на рисунке — корова или верблюд.
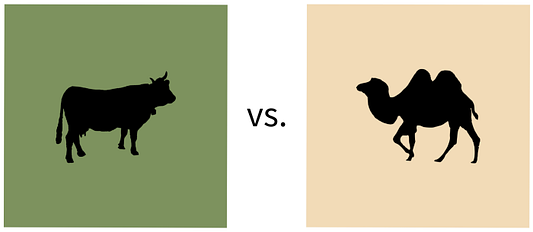
С этой целью мы обучаем бинарный классификатор с использованием перекрестной проверки и наблюдаем высокую точность наших тестовых данных. Отлично!
Но после тщательного анализа оказывается, что наш классификатор просто использовал цвет фона, чтобы установить метку “корова” или “верблюд”. Когда корову помещали на фон песочного цвета, модель всегда принимала ее за верблюда, и наоборот.
Итак, можем ли мы предположить, что коровы всегда будут наблюдаться на пастбищах, а верблюды — в пустынях? Скорее всего, нет. Этот простой пример показывает нам, насколько неточными при обобщении могут оказаться более сложные и важные модели.
1.2 Почему существующие методы недостаточно результативны?
Прежде чем погрузиться в решение этой проблемы, давайте разберемся, почему популярная обучающая парадигма методом разделения датасета на train и test неэффективна.
Классическая парадигма train/test в указанной выше работе называется эмпирической минимизацией риска (ERM). Используя ERM, мы объединяем наши данные в обучающие/тестовые наборы, “натаскиваем” нашу модель по всем функциям, проводим проверку с помощью тестовых наборов и возвращаем готовую модель, протестированную с наилучшей точностью (вневыборочно). Одним из примеров может служить разделение train/test по принципу 50/50.
Чтобы понять, почему ERM плохо обобщает данные, давайте рассмотрим три основных предположения, которыми руководствуется эта система, а затем разберем их поодиночке:
- Наши данные независимы и одинаково распределены (IID).
- По мере сбора большего количества данных соотношение между размером выборки n и количеством значимых признаков должно уменьшаться.
- Идеальная точность тестирования достижима только в том случае, если существует реализуемая модель с идеальной точностью обучения, которую можно построить.
На первый взгляд может показаться, что все эти три предположения верны. Однако (спойлер) часто это не так. И вот почему.
Возьмем первое предположение. Наши данные почти никогда не являются по-настоящему IID. На практике нужно так собирать данные, чтобы сохранялась связь между их точками. Например, все изображения верблюдов в пустынях должны быть сделаны в определенных частях мира.
Кстати, есть много случаев, когда данные являются “очень” IID. Однако вы должны учесть важный момент — вводит ли ваш сбор данных предвзятость и как он это делает.
Предположение №1: если наши данные не являются IID, первое предположение недействительно, и мы не можем случайным образом перемешивать наши данные. Важно учитывать, вводит ли ваш механизм генерации данных предвзятость.
Перейдем ко второму предположению. Если бы мы моделировали причинно-следственные связи, мы ожидали бы, что количество значимых признаков останется достаточно стабильным после определенного количества наблюдений. Другими словами, по мере сбора более качественных данных мы могли бы выявить истинные причинно-следственные связи и в конечном итоге идеально их сопоставить. Таким образом, большее количество данных никак не улучшило бы точность нашей модели.
Однако в случае с ERM это редко бывает. Поскольку мы не можем определить, является ли связь причинно-следственной, большее количество данных часто может привести к множеству ложных корреляций. Это явление еще известно как дилемма смещения-дисперсии.
Предположение № 2. При использовании ERM количество значимых признаков, вероятно, будет увеличиваться по мере увеличения размера выборки, поэтому наше второе предположение недействительно.
Наконец, наше третье предположение гласит, что у нас есть возможность построить “идеальную” модель. Если мы не располагаем данными или надежными методами моделирования, это предположение можно признать неверным. Однако, если мы не знаем, что это неправда, мы всегда предполагаем обратное.
Предположение №3. Мы предполагаем, что оптимальная модель может быть реализована для достаточно больших датасетов, поэтому предположение № 3 справедливо.
В работе исследователей обсуждаются методы, не связанные с ERM, но они также не соответствуют требованиям по целому ряду причин. Главную мысль вы уловили.
3. Инвариантная минимизация риска как решение проблемы
Инвариантная минимизация риска (IRM) способна справиться со всеми задачами, перечисленными выше. IRM — это парадигма обучения, оценивающая причинно-следственные предикторы из нескольких учебных сред. Поскольку мы учимся на разных средах данных, мы с большей вероятностью сможем обобщить новые OOD-данные.
Как же нам это сделать? Мы используем теорию, согласно которой причинность опирается на инвариантность.
Вернемся к нашему примеру. Допустим, мы можем наблюдать коров и верблюдов в их пастбищных и пустынных местах обитаниях в 95% случаев, поэтому, если мы будем подгонять цвет фона, мы достигнем 95%-ной точности результата. Что ж, это довольно неплохо.
Но давайте вспомним основное понятие из сферы рандомизированных контролируемых испытаний, а именно — противоречие фактам. Если мы наблюдаем контрпример к гипотезе, мы опровергаем ее. Таким образом, если мы увидим хотя бы одну корову в песчаной местности, мы можем сделать вывод, что песчаный фон не обязательно говорит о наличии верблюдов.
К слову сказать, строгий принцип противоречия фактам может быть довольно суровым. Мы используем этот принцип в нашей функции потерь и жестко пресекаем случаи ложных прогнозов наших моделей в определенной среде.
Например, рассмотрим набор сред, каждая из которых соответствует конкретной стране. Предположим, что в 9 из 10 этих стран коровы живут на пастбищах, а верблюды — в пустынях, а в 10-й — наоборот. Если за основу обучения мы взяли эту 10-ю среду и наблюдаем множество контрпримеров, модель понимает, что фон не является причиной для установления метки “корова” или “верблюд”. Таким образом, значимость этого предиктора понижается.
2.1 Метод
Теперь, когда вы понимаете, что такое IRM, давайте перейдем к математическим вычислениям для реализации этой системы.
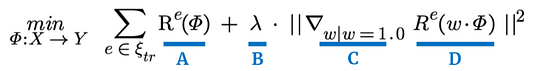
На рис. 2 показано выражение оптимизации. Как видно из сложения, мы стремимся минимизировать суммированное значение во всех учебных средах.
Величина “А” означает нашу точность прогнозирования в данной обучающей среде, где “фи” (𝛷) означает преобразование данных, таких как log, или же преобразование ядра в более высокие размерности. R — это функция риска нашей модели в условиях данной среды e. Обратите внимание, что функция риска — это просто среднее значение функции потерь. Классическим примером этого является среднеквадратичная ошибка (MSE).
Значение “B” — это просто положительное число, которое используется для масштабирования нашей величины инвариантности. Помните, мы говорили, что строгий принцип противоречия фактам может быть слишком суров? Здесь мы можем регулировать уровень нашей суровости. Если лямбда (λ) равна 0, мы не заботимся об инвариантности и просто оптимизируем точность. Если λ велика, для нас очень важна инвариантность и мы принимаем соответствующие корректирующие меры.
Наконец, значения “C” и “D” выражают инвариантность нашей модели в учебных средах. Не будем слишком вдаваться в подробности. Скажем только, что “C” — это вектор градиента нашего линейного классификатора w, значение которого по умолчанию равно 1. “D” — риск этого линейного классификатора w, умноженный на преобразование данных (𝛷). И вся эта величина представляет собой квадрат расстояния вектора градиента.
В работе подробно рассказывается об этих величинах, поэтому, если хотите узнать больше, ознакомьтесь с разделом 3.
Таким образом, “A” — это точность нашей модели, “B” — положительное число, показывающее уровень важности инвариантности для нас, а “C”/”D” — инвариантность нашей модели. Если мы минимизируем это выражение, мы найдем модель, которая будет работать только относительно причинно-следственных связей, обнаруженных в наших учебных средах.
2.2 Дальнейшее развитие IRM
К сожалению, парадигма IRM, изложенная здесь, работает только для линейных случаев. Преобразование данных в многомерное пространство может создать эффективные линейные модели, однако некоторые связи в основе своей остаются нелинейными. Авторы будут работать над нелинейными применениями системы в дальнейшем.
Если вы хотите оставаться в курсе исследований в этой сфере, ознакомьтесь с работами следующих авторов: Мартина Аржовского, Леона Бутту, Ишаана Гулражани и Девида Лопес-Паса.
Это и есть наш метод. Неплохо, правда?
3. Примечания по внедрению
- Вот пакет PyTorch.
- IRM лучше всего подходит для неизвестных причинно-следственных связей. Если есть известные связи, вы должны учитывать их в структуре модели. Известный пример — операции свертки для сверточных нейронных сетей (CNN).
- IRM обладает большим потенциалом для неконтролируемых моделей и обучения с подкреплением. Интересным способом применения является проверка справедливости модели.
- Оптимизация довольно сложна, потому что существует две величины минимизации. В работе описывается преобразование, делающее оптимизацию выпуклой, но только в случае линейного применения.
- IRM устойчива к незначительным ошибкам спецификации модели, поскольку она изменяется в зависимости от ковариаций обучающих сред. Таким образом, хотя “идеальная” модель и является совершенной, выражение минимизации устойчиво к небольшим погрешностям, допускаемым человеком.
Читайте также:
- Распознавание звуков с помощью глубокого обучения
- Создаем краткое содержание текста с помощью Python без NLP
- Глубокие нейросети: руководство для начинающих
Читайте нас в Telegram, VK и Яндекс.Дзен
Перевод статьи Michael Berk: How to make Deep Learning Models Generalize Better






