Для чего нужна математическая мультипликация?
Вы когда-нибудь пытались освоить математические концепции алгоритма машинного обучения с помощью образовательного ресурса 3Blue1Brown? 3Blue1Brown — это знаменитый математический канал на YouTube, созданный Грантом Сандерсоном. Многим он полюбился из-за отличных объяснений Гранта и классной анимации.
А здесь этот же канал с переводами на русский.
Было бы здорово узнать, как создается эта математическая мультипликация, чтобы научиться делать подобные ролики для объяснения тех или иных понятий науки о данных своим коллегам или подписчикам.
К счастью, Грант сделал пакет на языке Python под названием manim, который позволяет создавать математическую мультипликацию или изображения с использованием Python. В этой статье вы узнаете, как с помощью manim создавать математическую мультипликацию, подобную той, что показана ниже.

Что такое Manim?
Manim — это движок точной анимации, предназначенный для создания образовательных математических видеороликов. Обратите внимание, что есть две версии manim: первая создана Грантом, а вторая дублировала первую и поддерживается сообществом Manim Community.
Будем использовать версию, поддерживаемую сообществом Manim, так как эта версия обновляется чаще и лучше тестируется, чем версия Гранта.
Чтобы установить зависимости для пакета, загляните в документацию. После установки зависимостей введите:
pip install manim
Приступим
Создадим синий увеличивающийся квадрат
Код для создания анимации находится внутри метода construct класса, определяемого в Scene .
from manim import *
class PointMovingOnShapes(Scene):
def construct(self):
square = Square(color=BLUE) # Квадрат создается
square.flip(RIGHT) # Квадрат транспонируется вправо
square.rotate(-3 * TAU / 8) # Квадрат поворачивается -3/8 * 2*PI
# Воспроизводится анимация с увеличивающимся квадратом
self.play(GrowFromCenter(square))Сохраняем приведенный выше скрипт как start.py . Теперь запускаем команду для генерирования видео для скрипта:
$ manim -p -ql start.py PointMovingOnShapes
И видео под названием PointMovingOnShapes.mp4 будет сохранено у вас в локальном каталоге. Вот что вы должны увидеть:

Пояснения к приведенным выше параметрам:
-p: воспроизведение видео после того, как оно сгенерировано;-ql: генерирование видео с низким качеством.
Для генерирования видео с высоким качеством используем -qh.
Для создания вместо видео гифки добавляем в команду -i:
$ manim -p -ql -i start.py PointMovingOnShapes
Превратим квадрат в окружность
Одного квадрата будет мало. Делаем из него окружность:

А вот и код для создания этой анимации:
from manim import *
class PointMovingOnShapes(Scene):
def construct(self):
# Создается квадрат
square = Square(color=BLUE)
square.flip(RIGHT)
square.rotate(-3 * TAU / 8)
# Создается окружность
circle = Circle()
circle.set_fill(PINK, opacity=0.5) # задаются цвет и прозрачность
# Создается анимация
self.play(GrowFromCenter(square))
self.play(Transform(square, circle)) # квадрат превращается в окружность
self.wait() # несколько секунд ожиданияПолный список фигур смотрите здесь.
Настроим Manim под себя
Не хотите черный фон? Тогда превращаем его в серый

с помощью config.background_color:
from manim import *
config.background_color = DARK_GRAYДругие способы настройки manim смотрите здесь.
Для чего еще используют Manim?
Напишем математические уравнения с подвижной рамкой
Создаем анимацию, которая записывает математические уравнения с помощью подвижной рамки:

class MovingFrame(Scene):
def construct(self):
# Пишутся уравнения
equation = MathTex("2x^2-5x+2", "=", "(x-2)(2x-1)")
# Создается анимация
self.play(Write(equation))
# Добавляются подвижные рамки
framebox1 = SurroundingRectangle(equation[0], buff=.1)
framebox2 = SurroundingRectangle(equation[2], buff=.1)
# Создается анимация
self.play(Create(framebox1)) # с созданием рамки
self.wait()
# frame 2 сменяет frame 1
self.play(ReplacementTransform(framebox1, framebox2))
self.wait()или записываем пошагово, как решить уравнение:

class MathematicalEquation(Scene):
def construct(self):
# Пишутся уравнения
equation1 = MathTex("2x^2-5x+2")
eq_sign_1 = MathTex("=")
equation2 = MathTex("2x^2-4x-x+2")
eq_sign_2 = MathTex("=")
equation3 = MathTex("(x-2)(2x-1)")
# Каждое уравнение или знак помещается в соответствующее положение
equation1.next_to(eq_sign_1, LEFT)
equation2.next_to(eq_sign_1, RIGHT)
eq_sign_2.shift(DOWN)
equation3.shift(DOWN)
# Нижние уравнения приводятся в соответствие с верхними
eq_sign_2.align_to(eq_sign_1, LEFT)
equation3.align_to(equation2, LEFT)
# Уравнения и знак группируются
eq_group = VGroup(equation1, eq_sign_1, equation2, eq_sign_2, equation3)
# Создается анимация
self.play(Write(eq_group))
self.wait()Перемещение и наезд камеры
Настраиваем камеру и выбираем, какую часть уравнений увеличить с помощью класса, наследуемого от объекта MovingCameraScene.
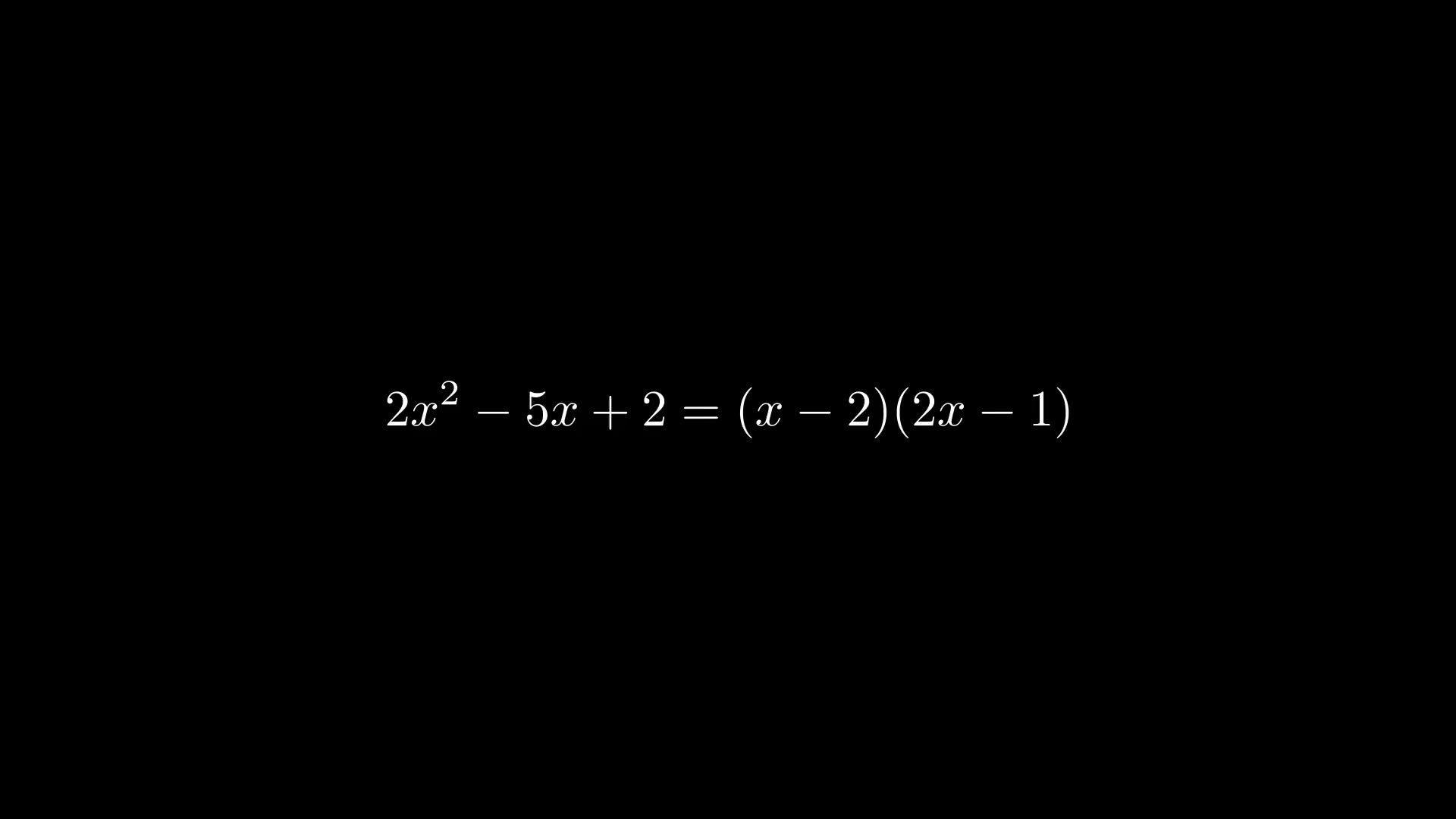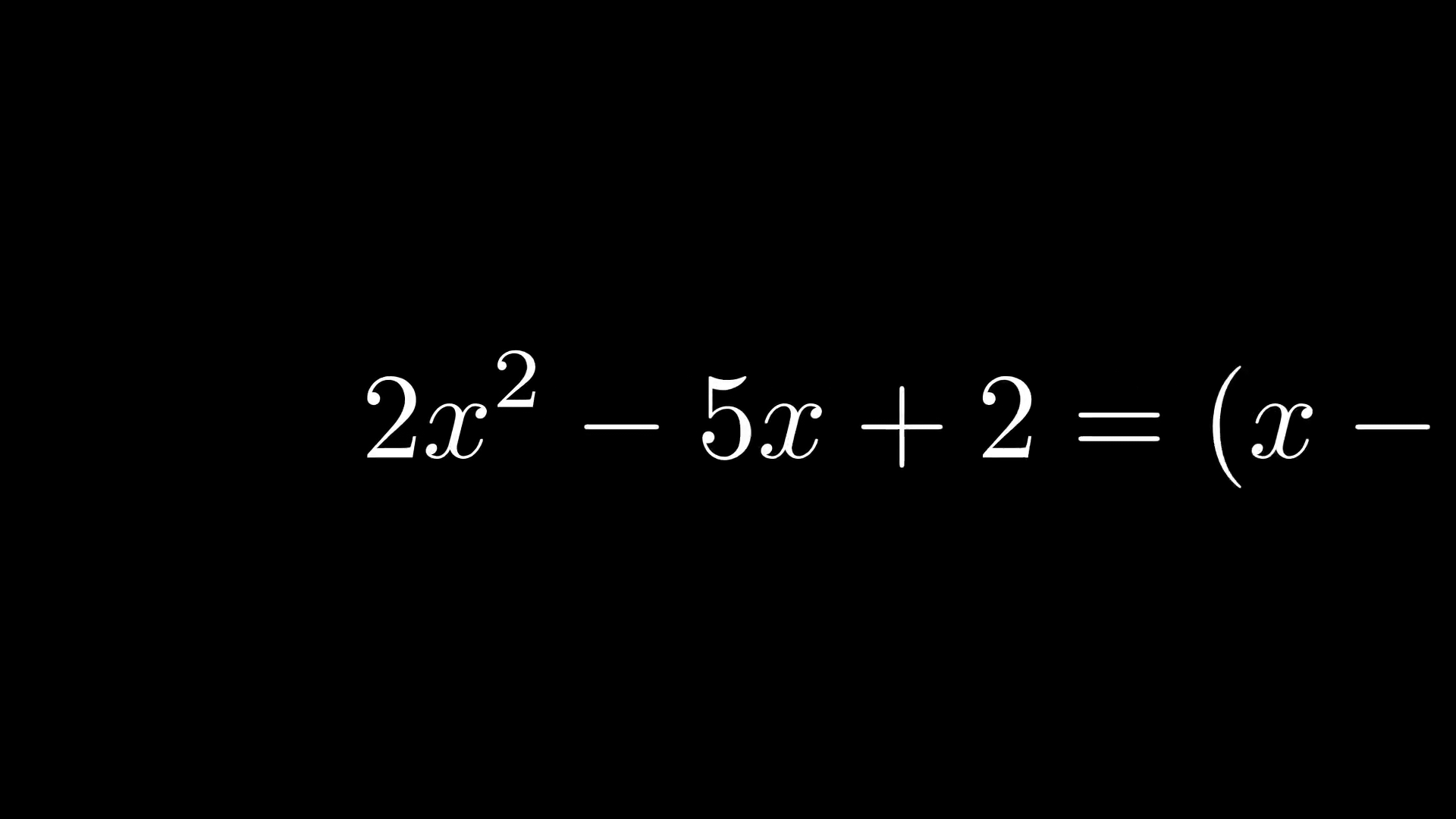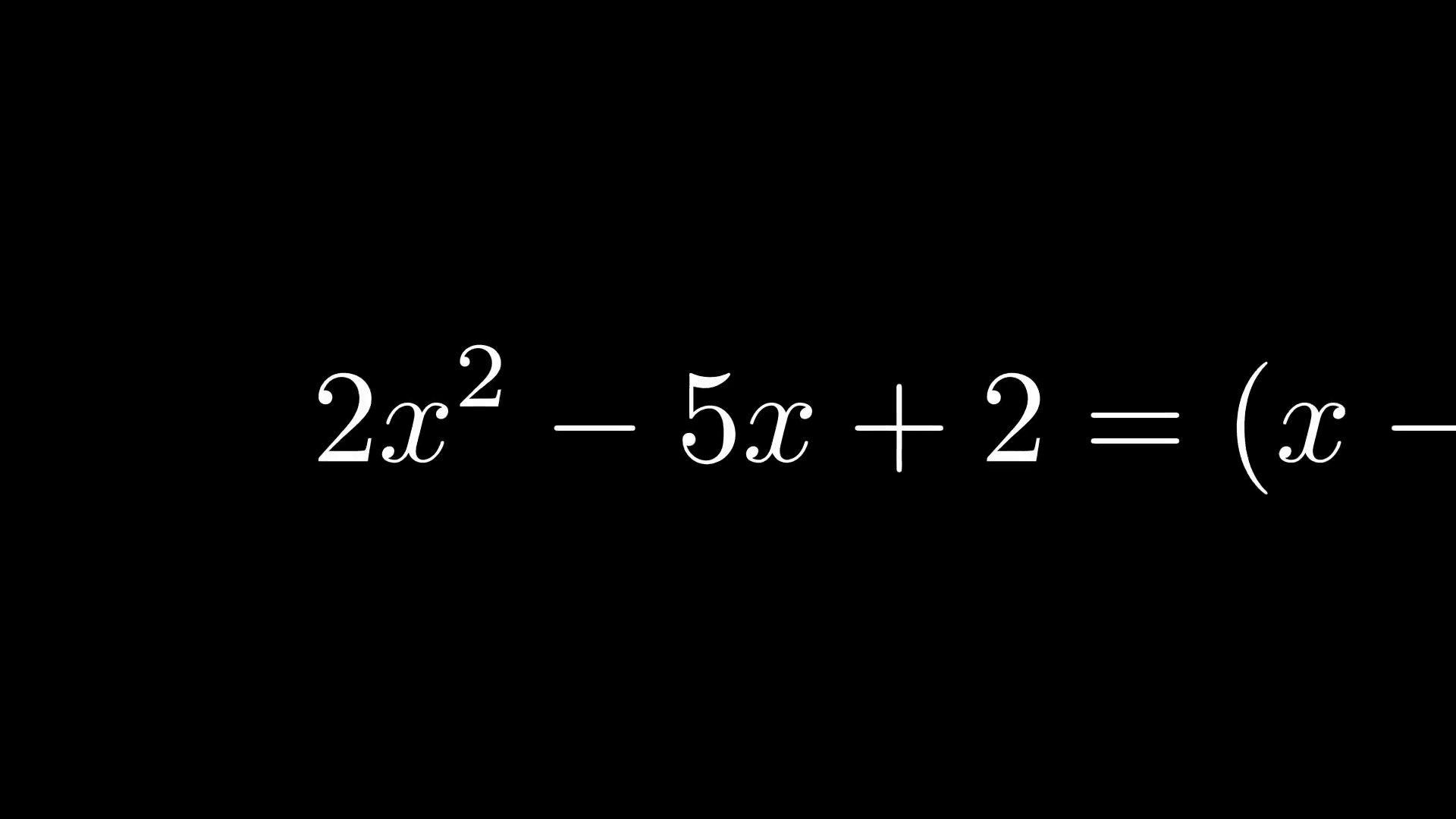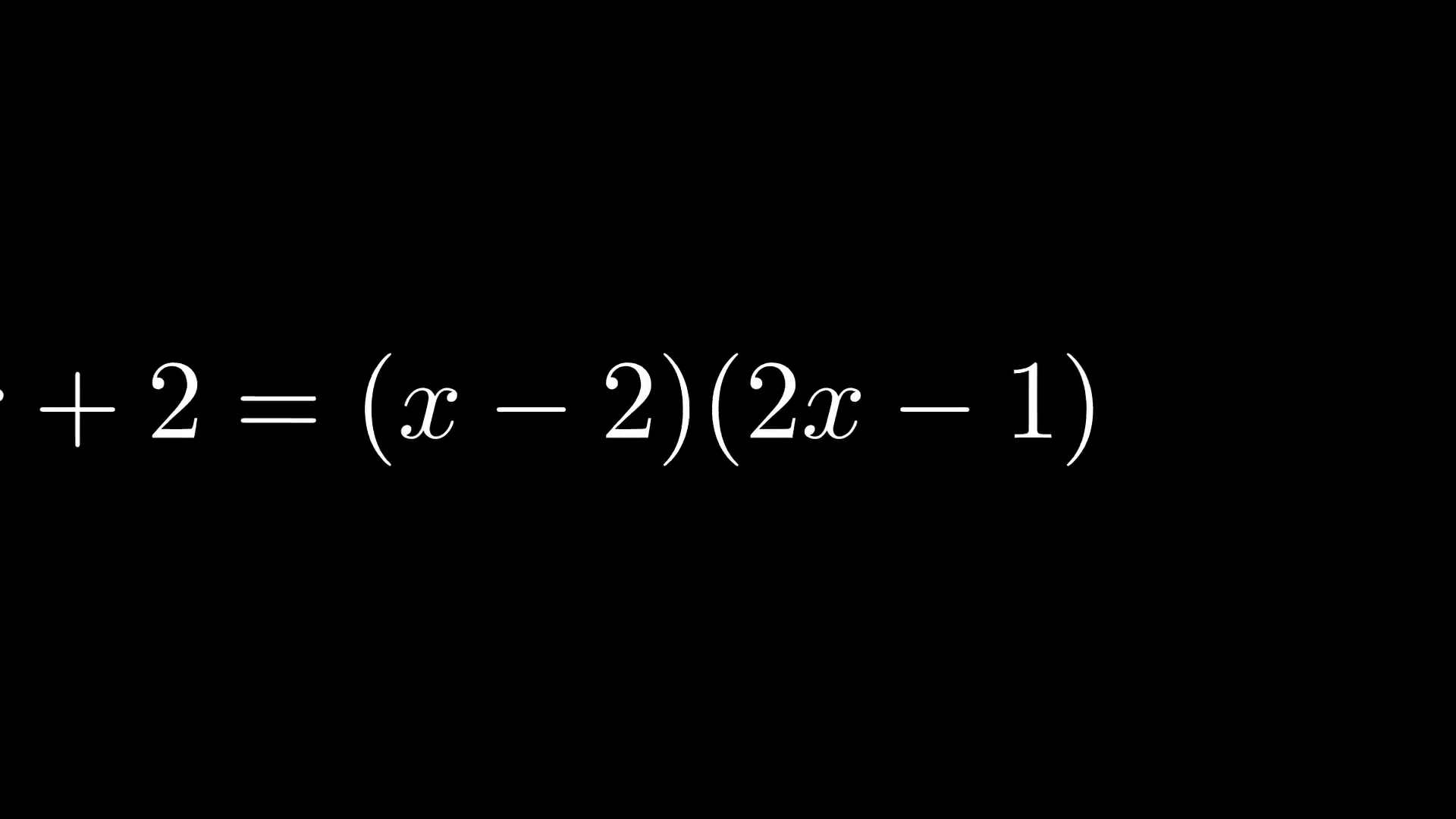
class MovingAndZoomingCamera(MovingCameraScene):
def construct(self):
# Пишутся уравнения
equation = MathTex("2x^2-5x+2", "=", "(x-2)(2x-1)")
self.add(equation)
self.play(self.camera.frame.animate.move_to(equation[0]).set(width=equation[0].width*2))
self.wait(0.3)
self.play(self.camera.frame.animate.move_to(equation[2]).set(width=equation[2].width*2))Графики
Используем manim для создания аннотированного графика:
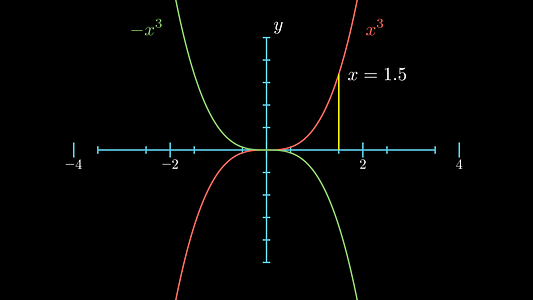
class Graph(GraphScene):
def __init__(self, **kwargs):
GraphScene.__init__(
self,
x_min=-3.5,
x_max=3.5,
y_min=-5,
y_max=5,
graph_origin=ORIGIN,
axes_color=BLUE,
x_labeled_nums=range(-4, 4, 2), # x тикеры
y_labeled_nums=range(-5, 5, 2), # y тикеры
**kwargs
)
def construct(self):
self.setup_axes(animate=False)
# Рисуются графики
func_graph_cube = self.get_graph(lambda x: x**3, RED)
func_graph_ncube = self.get_graph(lambda x: -x**3, GREEN)
# Создаются метки
graph_lab = self.get_graph_label(func_graph_cube, label="x^3")
graph_lab2 = self.get_graph_label(func_graph_ncube, label="-x^3", x_val=-3)
# Создается вертикальная линия
vert_line = self.get_vertical_line_to_graph(1.5, func_graph_cube, color=YELLOW)
label_coord = self.input_to_graph_point(1.5, func_graph_cube)
text = MathTex(r"x=1.5")
text.next_to(label_coord)
self.add(func_graph_cube, func_graph_ncube, graph_lab, graph_lab2, vert_line, text)
self.wait()Если надо получить изображение последней рамки scene, добавляем к команде -s:
manim -p -qh -s more.py Graph
Анимируем процесс настройки осей координат, установив значение animate=True:
def construct(self):
self.setup_axes(animate=True)
################### Ниже то же самое, что и выше ###################
$ manim -p -qh more.py Graph
Перемещение объектов
Задействуем VGroup для группировки различных объектов Manim и их совместного перемещения:
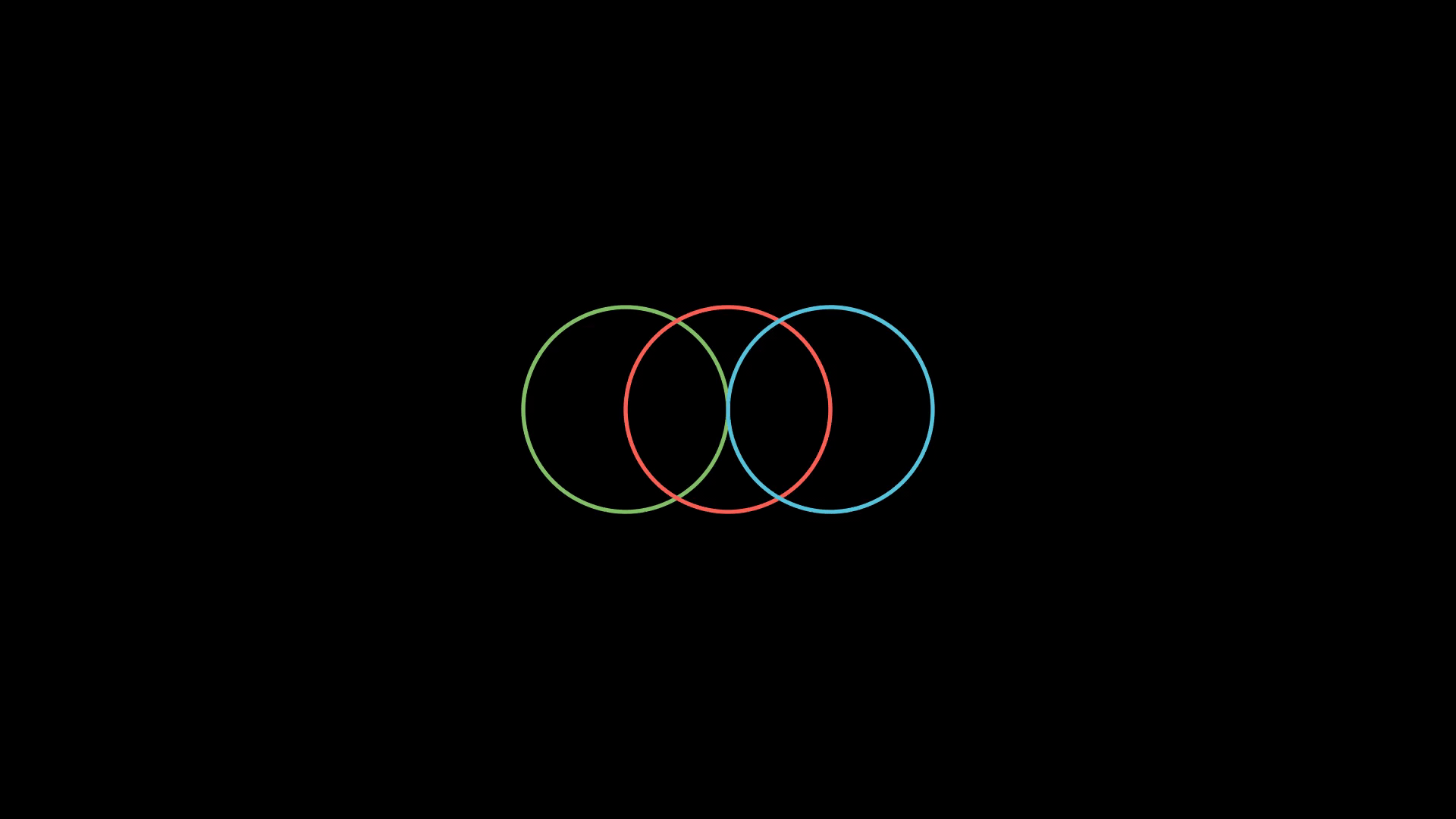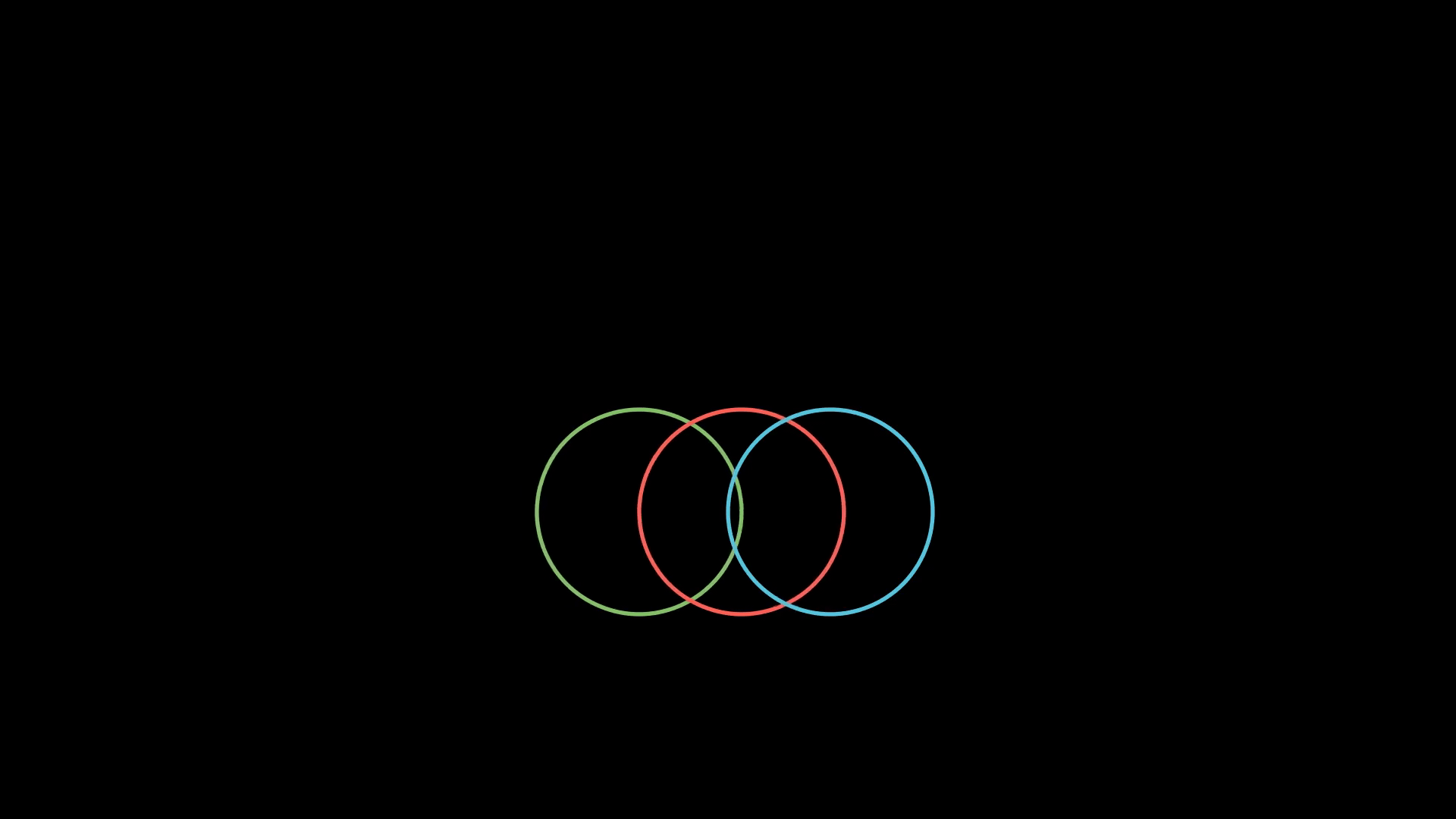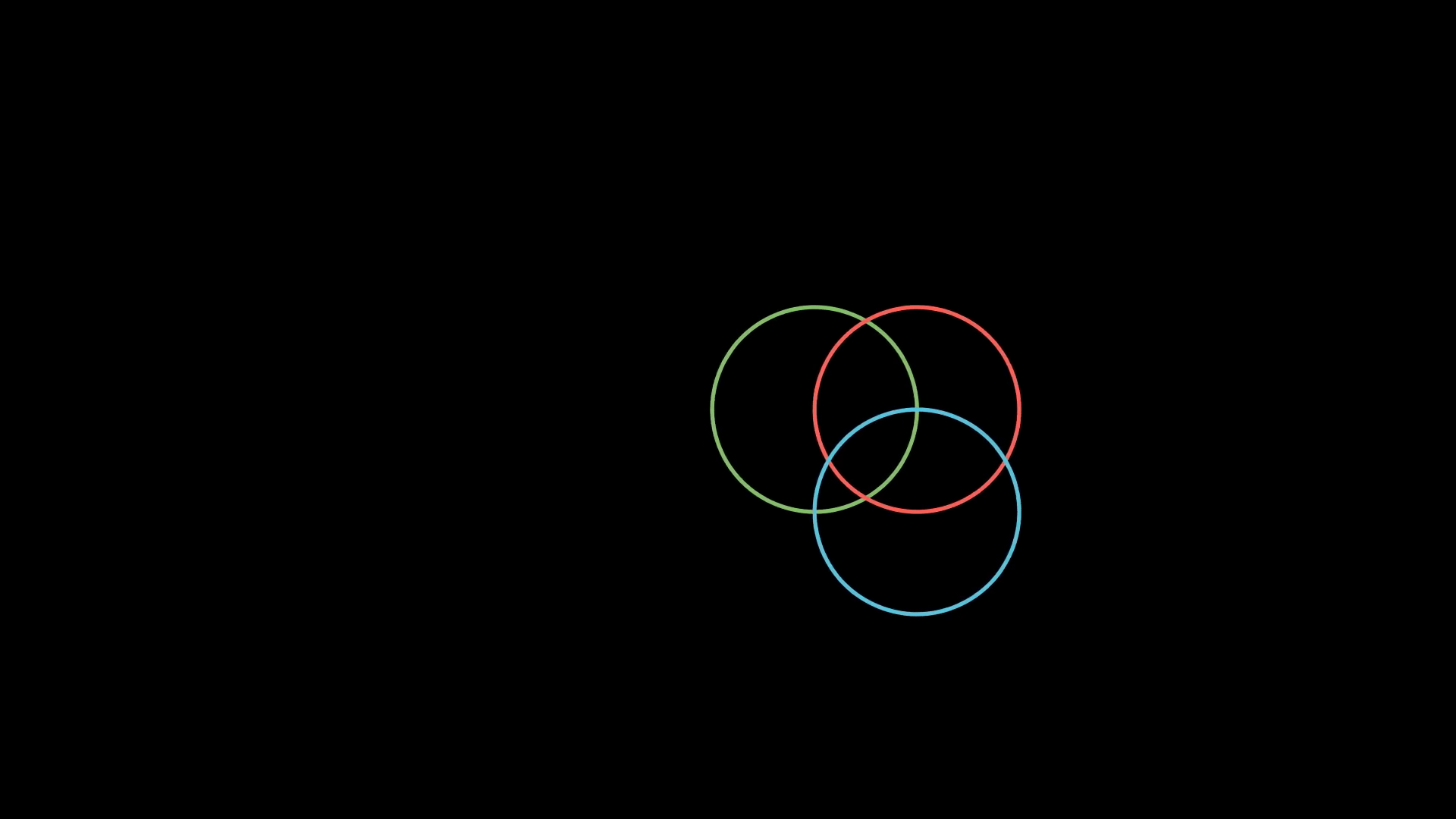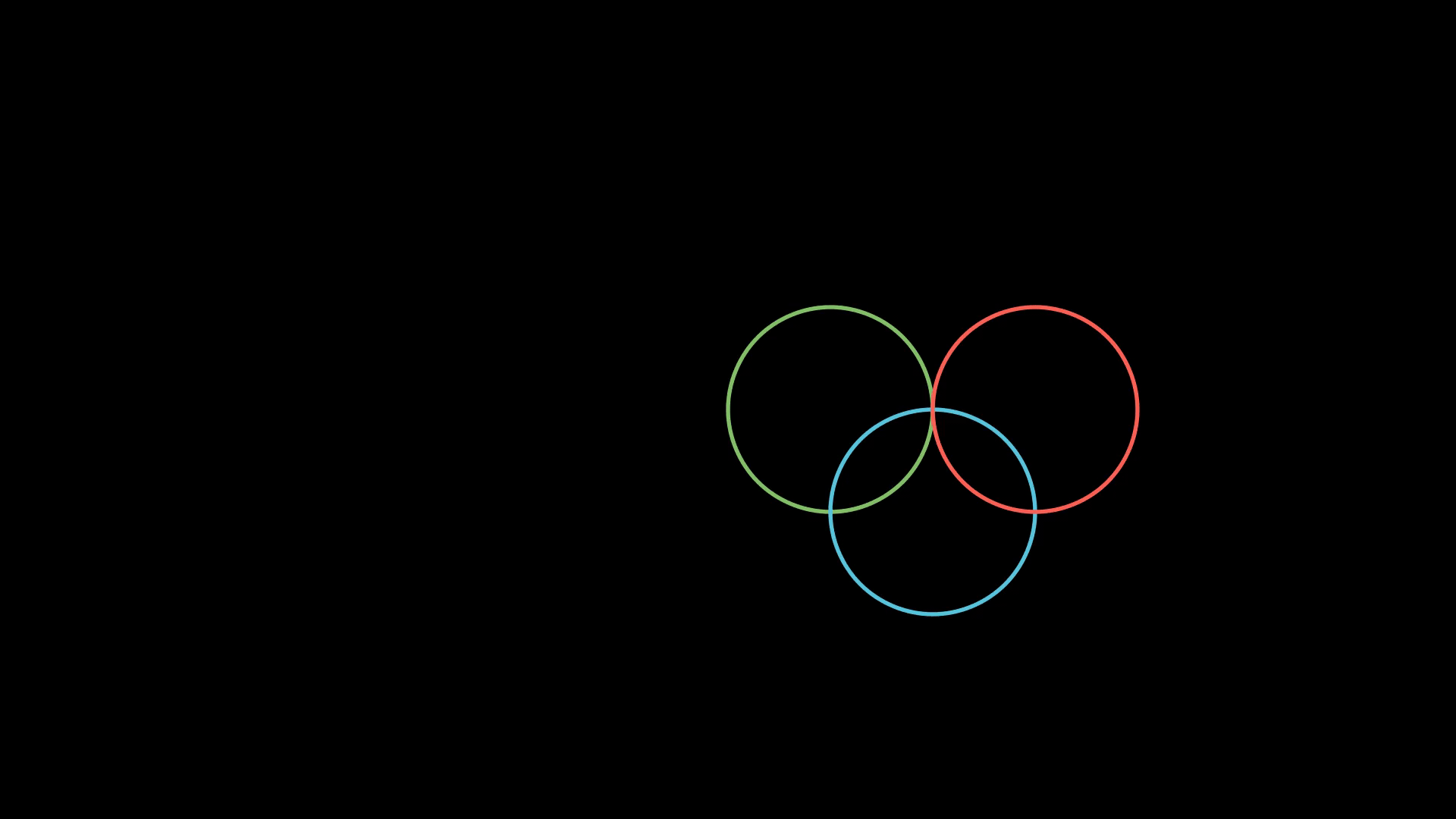
class GroupCircles(Scene):
def construct(self):
# Создаются окружности
circle_green = Circle(color=GREEN)
circle_blue = Circle(color=BLUE)
circle_red = Circle(color=RED)
# Задаются исходные позиции
circle_green.shift(LEFT)
circle_blue.shift(RIGHT)
# Создаются две разные группы
gr = VGroup(circle_green, circle_red)
gr2 = VGroup(circle_blue)
self.add(gr, gr2) # две группы добавляются в scene
self.wait()
self.play((gr + gr2).animate.shift(DOWN)) # две группы сдвигаются вниз
self.play(gr.animate.shift(RIGHT)) # перемещается только одна группа
self.play(gr.animate.shift(UP))
self.play((gr + gr2).animate.shift(RIGHT)) # две группы сдвигаются вправо
self.play(circle_red.animate.shift(RIGHT))
self.wait()Trace Path
Используем TracedPath для создания следа движущегося объекта:

class TracedPathExample(Scene):
def construct(self):
# Создается окружность и точка
circ = Circle(color=BLUE).shift(4*LEFT)
dot = Dot(color=BLUE).move_to(circ.get_start())
# Точка и окружность группируются
rolling_circle = VGroup(circ, dot)
trace = TracedPath(circ.get_start)
rolling_circle.add_updater(lambda m: m.rotate(-0.3)) # Окружность поворачивается
self.add(trace, rolling_circle) # след и вращающаяся окружность добавляются в scene
# Окружность сдвигается на 8*RIGHT
self.play(rolling_circle.animate.shift(8*RIGHT), run_time=4, rate_func=linear)Подведем итоги
Поздравляем! Вы только что научились использовать manim и узнали, на что он способен. Напомним, что manim работает с тремя видами объектов.
- Mobjects. Объекты, отображающиеся на экране, такие как
Circle(окружность),Square(квадрат),Matrix(матрица),Angle(угол) и т. д. - Scenes. Холст для анимации, такой как
Scene(сцена),MovingCameraScene(сцена с движущейся камерой) и т. д. - Animations. Действия, применяемые к объектам Mobjects для создания анимации, например
Write(написание),Create(создание),GrowFromCenter(увеличение),Transform(преобразование) и т. д.
Manim способен на гораздо большее, чем то, о чем нам удалось рассказать. Лучший способ научиться — практиковаться, поэтому рекомендую попробовать примеры из этой статьи и заглянуть в руководство по manim.
Исходный код находится здесь.
Читайте также:
- Как отслеживать события файловой системы в Python
- Функциональное программирование на Python
- 3 инструмента для отслеживания и визуализации выполнения кода на Python
Читайте нас в Telegram, VK и Яндекс.Дзен
Перевод статьи Khuyen Tran: How to Create Mathematical Animations like 3Blue1Brown Using Python