А может быть сможете их перехитрить?
В повседневной жизни мы постоянно сталкиваемся с ситуациями неопределенности. Так, по крайней мере подсознательно, мы постоянно встречаемся с вероятностями. Более того, нам кажется, что у нас хорошо развито интуитивное чувство вероятности. Но так ли это на самом деле?
Мы знаем, что, если подбросить монетку 100 раз, то она упадет около 50 раз решкой вверх и 50 раз вверх орлом. Также понятное дело, что вероятность наткнуться на друга в отпуске за границей очень невысокая, хотя и не равно нулю. Однако существуют ситуации, в которых верные предсказания в соответствии с теорией вероятности совершенно не согласуются с теми, которые подсказывает интуиция.
Давайте погрузимся в пять парадоксов теории вероятности и статистики, которые предлагают абсурдные на вид результаты. Тем не менее они достоверны.
1. Парадокс дней рождения

Вы на вечеринке у друга, на которой присутствует 30 человек. Какова вероятность, что у двух из них день рождения будет в один и тот же день? Что подсказывает вам интуиция? Возможно, что какая-то вероятность имеется, однако она очень низкая?
Итак, условие парадокса дней рождения звучит следующим образом:
Сколько людей должно быть на вечеринке, чтобы вероятность того, что у двоих из них дни рождения будут в один день, составляла как минимум 50 процентов?
Парадокс предполагает, что вероятность того, что каждый из дней в году в равной степени будет днем рождения случайного человека.
Ответ поражает: всего 23! На вечеринки у вашего друга, на которой присутствует 30 человек, вероятность того, что у двух человек будут дни рождения в один день, составляет более 70%!
2. Парадокс Симпсона
Предположим, что мы бизнес-партнеры. У нас есть пять разных кофеен по всему городу. В качестве маркетинговой стратегии мы выдаем ваучеры самым лояльным клиентам в надежде на то, что они вернутся и купят еще больше кофе.
Однако возникает спор о том, каким должен быть номинал ваучеров. Чтобы прийти к наилучшему решению, мы выдаем ваучеры с разными номиналами. Мы собираем данные о том, сколько прибыли получили с каждого лояльного клиента в течение следующего месяца.
После одного месяца все кажется понятным: для каждой из пяти наших кофеен тенденция одинаковая. Чем больше номинал ваучера, тем больше прибыли мы получили от соответствующего покупателя.
Однако при общем рассмотрении данных из пяти кофеен вместе наблюдается прямо противоположная тенденция: чем больший номинал у ваучера, тем меньше прибыли принес клиент. Как такое может быть?
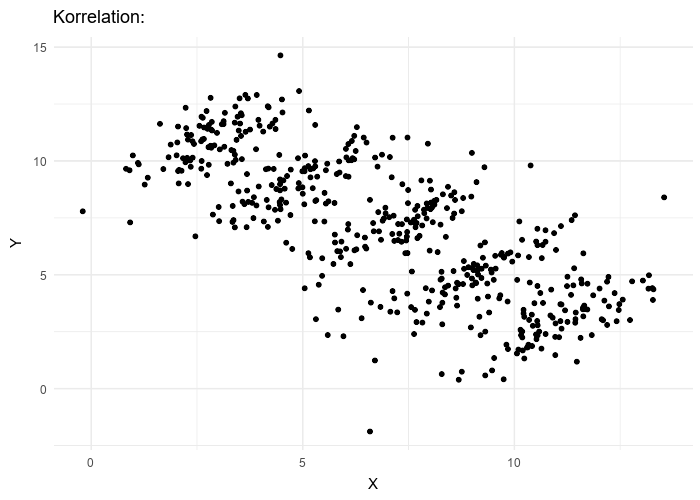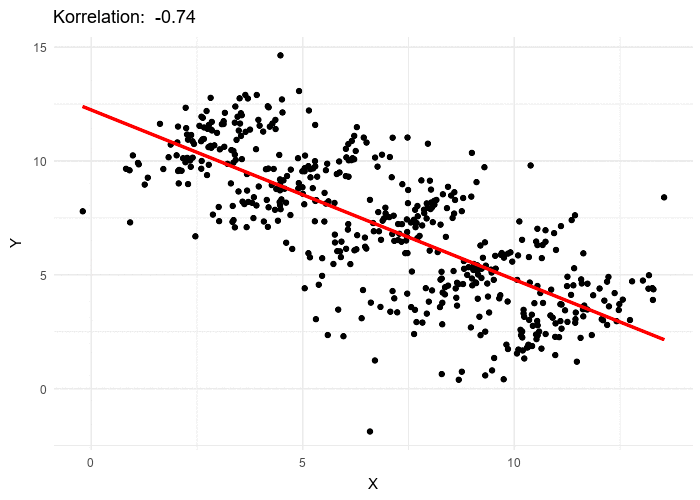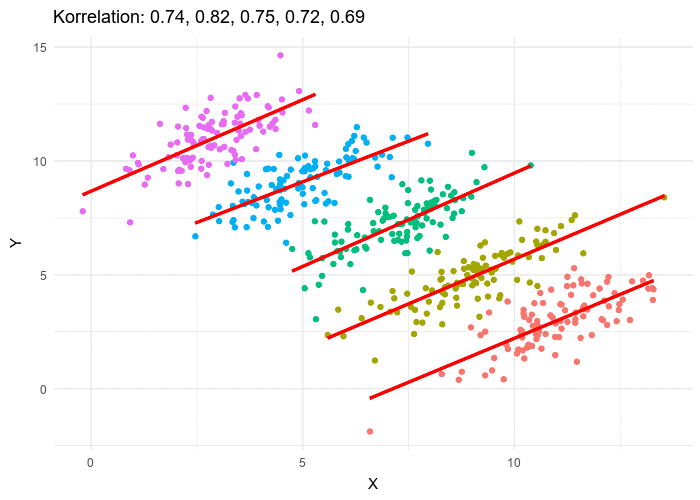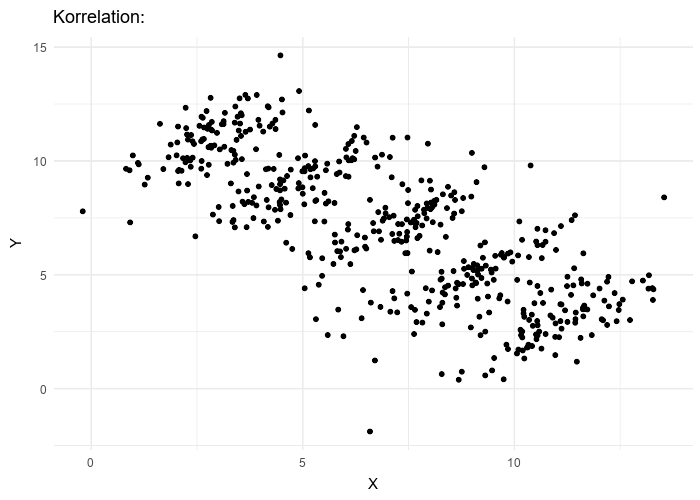
Это и есть Парадокс Симпсона:
Тенденция, наблюдаемая в разных группах, может пропасть при объединении данных.
3. Парадокс коробок Бертрана
Если вы знакомы с парадоксом Монти Холла, то этот парадокс очень на него похож. Напротив нас стоят три коробки:

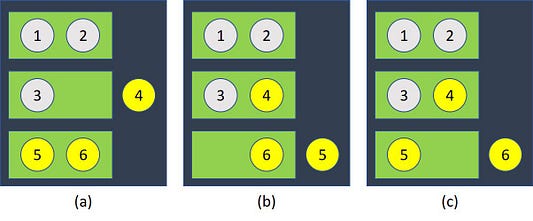
В одной коробке лежат две серебряные монеты, во второй — две золотые, а в третьей — одна золотая и одна серебряная. Мы не знаем, в какой коробке какие монеты. Итак, выбираем случайную коробку и вслепую достаем одну монету из этой коробки.Она золотая!
Вопрос такой:
Какова вероятность того, что вторая монета в выбранной нами коробке также золотая?
Наивным (и неверным) предположением многих людей при первом столкновении с этой задачей будет вероятность в ½. Что-то подсказывает: если мы вытянули золотую монету, то эта коробка содержит либо 2 золотые, либо одну золотую и одну серебряную монету. В первом случае мы бы вытянули другую золотую монету, а во втором — нет. Таким образом можно предположить, что вероятность составляет ½.
Однако реальная вероятность — ⅔.
Причина этому — первая вытянутая золотая монета могла быть либо единственной золотой монетой в ящике с одной золотой и одной серебряной монетой, первой золотой монетой в ящике с золотыми монетами либо второй золотой монетой в ящике с золотыми монетами. И в двух из этих вариантов мы вытянем золотую монету:
4. Парадокс пари (Парадокс галстуков)
После новогодних праздников вы возвращаетесь в офис в новом галстуке, который получили в подарок. Вашему коллеге Бобу также подарили на Новый год галстук. Никто из вас не знает цены своего галстука. Вы начинаете спорить насчет того, у кого галстук дороже.
Боб и вы заключаете пари: каждому из вас необходимо узнать цену своего галстука. Тот, чей галстук дороже, должен будет отдать его тому, чей галстук дешевле.

Боб думает, что спор в любом случае разрешится в его пользу:Его шансы выиграть или проиграть — 50/50. Если он проиграет, то он потеряет стоимость своего галстука. Если он победит, то выиграет больше, чем стоит его галстук.
Но со своей точки зрения вы можете построить такую же логическую цепочку и прийти к заключению, что спор будет в вашу пользу.
Но пари не может быть одновременно в вашу пользу и в пользу Боба. Так где же ошибка?
Чтобы решить Парадокс галстуков нужно включить цены галстуков в расчеты:пусть один галстук стоит 1000 рублей, а другой — 500 рублей. Если выиграет Боб, то его выигрыш составит галстук стоимостью 1000 рублей. Если он проиграет, это будет значить, что у него был более дорогой галстук, и он только что потерял 1000 рублей. Таким образом, потенциальный выигрыш отменяется, и такой спор по сути невыгоден никому.
5. Случайное блуждание
Этот факт не считается парадоксом, но он кажется таким захватывающим и удивительным, что должен быть в этом списке.
Представьте муравья на бесконечном листе бумаги. Каждую секунду муравей случайным образом направляется в одном из четырех возможных направлений (вперед, назад, влево или вправо). Вероятности, что он пойдет в каждом из этих направлений, равны. Этот сценарий называется случайной симметричной 2D-прогулкой, так как бумага двумерная.
Также можно представить, что муравей ползет не по листу бумаги, а по нитке. В этом случае муравей может двигаться лишь вперед и назад, и мы знакомимся со случайной 1D-прогулкой.
Таким же образом можно представить случайную 3D-прогулку,где путешественник — это дрон или птица, которая случайным образом двигается в шести направлениях (вперед/назад, влево/вправо, вверх/вниз).
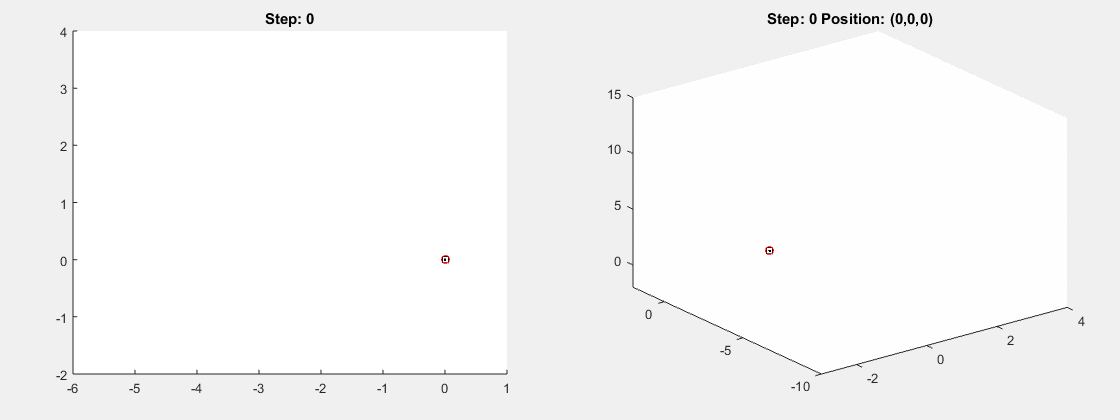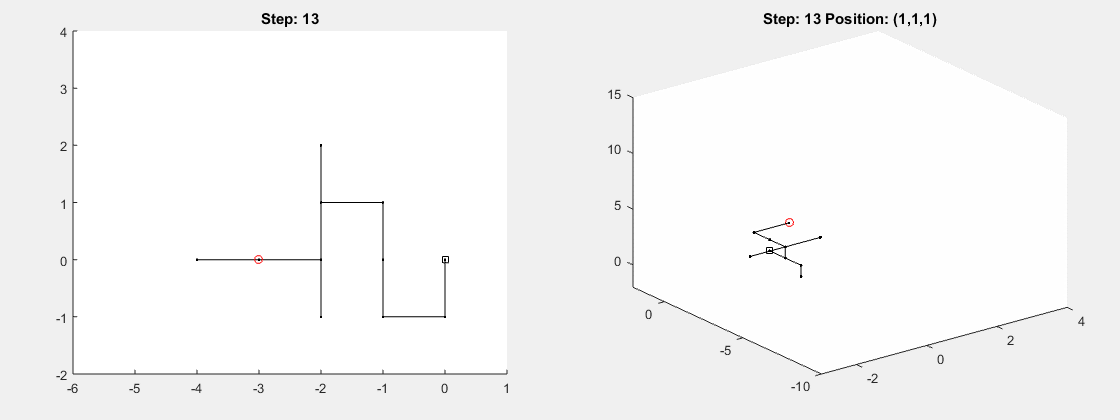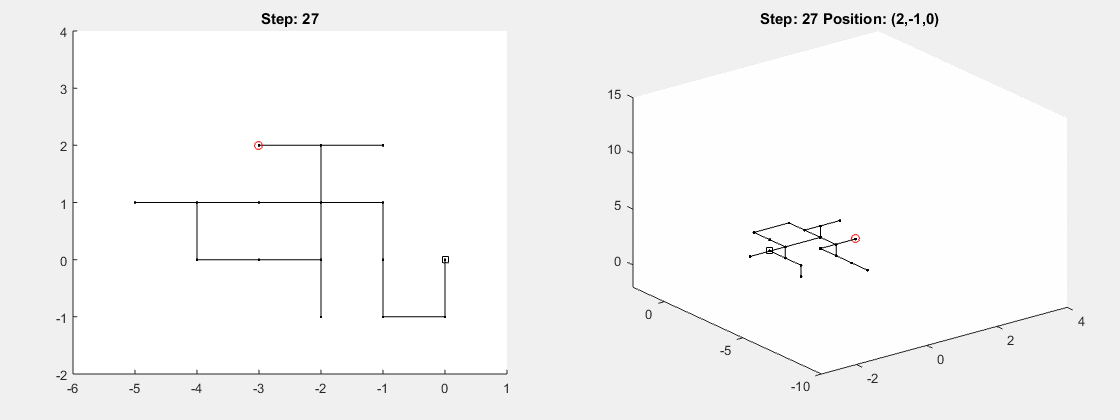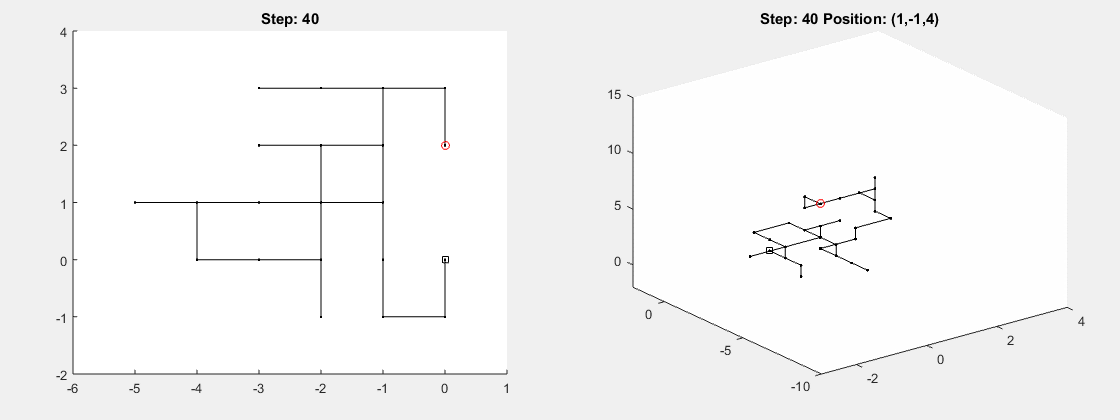
Вопрос такой:
Какова вероятность, что путешественник вернется в начальное положение?
Ответ удивляет: для муравья на нитке (1D) или на бумаге (2D) вероятность равна 1. Однако для птицы существует вероятность, что она улетит в бесконечное путешествие безвозвратно. Это утверждение также будет верно для 4, 5, 6-мерного мира.
Такие математические выводы ошеломляют. Можно смотреть на математическую логику, но очень сложно до конца понять ее на интуитивном уровне. Математик Сидзуо Какутани с улыбкой сказал по этому поводу:
Пьяный человек найдет дорогу домой, но пьяная птица может потеряться навсегда.
Спасибо за прочтение!
Читайте также:
- Математические операции над массивами и матрицами
- Плотность вероятности - это не сама вероятность
- Цепь Маркова
Читайте нас в Telegram, VK и Яндекс.Дзен
Перевод статьи Marcel Moosbrugger: Five Paradoxes With Probabilities That Will Puzzle You






