
Понятия вероятности и случайности затрагивают практически все аспекты нашей жизни. Большинство своих решений мы принимаем, исходя из вероятности наиболее благоприятных для нас событий. Поэтому стоит хотя бы мало-мальски разбираться в теории вероятностей и научиться применять ее законы при решении различных житейских задач.
Обычно первое, что приходит на ум при упоминании о теории вероятности, — это игральные кости или карты. И то, и другое часто ассоциируется с азартными играми или другими занятиями, где все решает Его Величество Случай. Интересно, что сам термин “случайность” довольно точно передает суть понятия вероятности. Если говорить кратко, вероятность — это степень возможности какой-либо случайности.
Аристотель как-то заметил: “Вероятно и то, что много происходит невероятного”. Если перевести этот афоризм на математический язык, то можно выразить понятие вероятности следующим образом:
P = (количество реальных исходов) / (суммарное число реальных и возможных исходов),
где P — вероятность наступления события.
Значение P всегда будет выражено дробным числом в интервале [0, 1] (умножив это число на 100, можно выразить его в процентах). Чем выше значение P, тем больше вероятность наступления события. Если P = 0, говорят о невозможности наступления события; если P = 1, безоговорочно утверждают, что событие произойдет.
Теперь рассмотрим несколько простых, но убедительных примеров того, как работает выведенная нами формула вероятности.
Какова вероятность выпадения “тройки” при игре в кости?
На этот вопрос можно относительно быстро ответить с помощью интуиции. Но давайте попробуем применить нашу формулу. Игральный кубик имеет 6 сторон, но только 1 сторона отображает число “три”. Подставляя эти данные в формулу вероятности, получаем: P(“три”) = 1/6.
Какова вероятность вытянуть валета из колоды карт?
Снова задаем себе вопросы: сколько всего карт в колоде и какое количество в ней валетов? Мы знаем, что в обычной колоде 52 карты, по 4 фигурных экземпляра каждой масти, то есть в общей сложности 4 валета. Следовательно, вероятность вытянуть валета равна 4/52 или 1/13.
Оба приведенных выше примера довольно просты. Но они вполне годятся для того, чтобы в общих чертах ознакомить с теорией вероятностей человека, не искушенного в математике. Для решения более сложных задач используются куда более мудреные методы матанализа.
Вероятность объединения и пересечения
Объединение — это один из двух распространенных типов сложных событий (когда речь идет о двух или более объединенных событиях). Мы определяем вероятность объединения событий X и Y как вероятность того, что произойдет либо X, либо Y, либо и то, и другое. Из этого определения вытекают две различные формулы для вычисления вероятности. Рассмотрим каждую из них.
Объединение взаимоисключающих событий
Если события X и Y не могут произойти одновременно, они считаются взаимоисключающими. В этом случае мы используем следующую формулу:
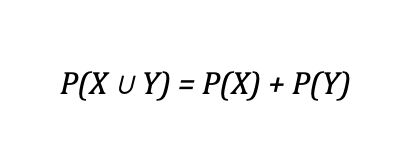
Предположим, что мы хотим вычислить вероятность выпадения “пятерки” или “шестерки” в ходе игры в кости. Эти события не могут произойти одновременно, поэтому нам просто нужно сложить значения обеих вероятностей. Вероятность выбросить “пятерку” равна 1/6; вероятность выбросить “шестерку” также равна 1/6; следовательно, вероятность выпадения “пятерки” или “шестерки” равна 1/3.
Объединение событий, не исключающих друг друга
В случае, когда X и Y не являются взаимоисключающими, используется следующая формула:
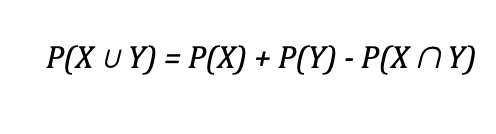
Как вы заметили, эта формула похожа на предыдущую, но с добавлением вероятности событий X и Y, связанных между собой символом, похожим на перевернутую букву U. Это называется пересечением — вторым из двух распространенных типов сложных событий. Вероятность пересечения двух событий определяется как вероятность того, что события X и Y произойдут одновременно.
Остановимся на формуле пересечения, так как она чрезвычайно важна при вычислении вероятности не исключающих друг друга событий.
Классический пример, демонстрирующий эту формулу, — игральные карты. Предположим, мы хотим определить вероятность вытянуть из колоды карту пиковой масти или даму. Зная о не исключающих друг друга событиях, мы можем предположить, что в колоде есть карта, которая одновременно является дамой и относится к пиковой масти. Сначала определяем вероятности выбора карты пиковой масти, дамы и пиковой дамы, которые составляют 13/52, 4/52 и 1/52 соответственно. Итоговое значение вероятности получаем путем сложения первых двух дробей и вычитанием из этой суммы третьей дроби. В результате выходит 16/52 или 4/13.
Пересечение независимых событий
Теперь, когда вы уже познакомились с концепцией пересечения, давайте углубимся в нее еще больше. Обычно мы имеем дело с пересечением независимых событий, когда вероятность одного из них не влияет на вероятность другого. В этом случае формула пересечения выглядит следующим образом:
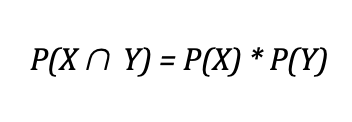
Например, если подбросить две монеты, то вероятность того, что обе они упадут решкой вверх, равна 0,5 * 0,5 = 0,25. Есть и альтернативный способ решения этой задачи. Для этого нужно вспомнить наше первое определение вероятности, представляющее собой соотношение количества происходящих событий к общему числу исходов. Сначала перечислим все возможные исходы при падении двух монет:
{H, H} , {H, T} , {T , H} , {T ,T}, где H — орел, T — решка.
Сколько исходов может быть с выпадением двух решек? Только один из четырех.
Условная вероятность
Условной считается вероятность события X при условии наступления события Y.
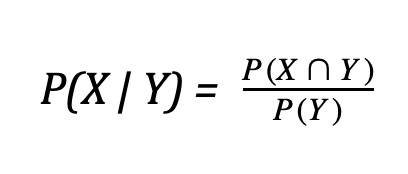
(Обратите внимание, что это уравнение включает в себя выражение для пересечения, которое можно вывести следующим образом: P(X | Y) * P(Y). Такая версия формулы пересечения используется для событий, которые не являются независимыми друг от друга).
Предположим, в деканат поступила информация о посещении практики 41 студентом в течение недели. Используя эти данные, декан построил график и получил следующую картину:
- из 22 первокурсников 9 посещали менее 3 дней, а 13 — более 3 дней;
- из 19 второкурсников 12 посещали менее 3 дней, а 7 — более 3 дней.
Поможем декану выяснить вероятность посещения менее 3 дней практики студентами при условии, что его интересуют в первую очередь первокурсники:
P(< 3 дней | первокурсники).
Сначала вычислим вероятность пересечения. Из общего числа студентов (мы знаем, что практику проходил 41 человек) 9 первокурсников посетили менее 3 дней, так что эта вероятность составляет 9 / 41. Второе, что нам нужно определить, — вероятность быть первокурсником. Она равна 22 / 41. Отсюда условная вероятность будет равна (9 / 41) / (22 / 41), или 9 / 22.
Подведем итоги
Теперь вы имеете представление об основных принципах применения теории вероятностей. Ее формулы пригодятся вам в любом месте, будь то студенческая аудитория или исследовательская лаборатория. Ее законы позволят вам не полагаться на случай. Вычисляя и сопоставляя свои шансы и риски, вы сможете принимать верные решения в области медицины, статистики, финансов и многих других.
Читайте также:
- Годовой план изучения науки о данных
- Что нужно знать, чтобы начать заниматься квантовыми вычислениями
- Статистические типы данных, используемые в машинном обучении
Читайте нас в Telegram, VK и Яндекс.Дзен
Перевод статьи Albert Ming, An Introduction to Probability and the World of Chance






