В течение последних десятилетий машинное обучение оказало огромное влияние на весь мир, и его популярность только набирает обороты. Все больше людей увлекается подотраслями этой науки, например нейронными сетями, которые разрабатываются по принципам функционирования человеческого мозга. В этой статье мы разберем код Python для простой нейронной сети, классифицирующей векторы 1х3, где первым элементом является 10.
Шаг 1: импорт NumPy, Scikit-learn и Matplotlib
import numpy as np
from sklearn.preprocessing import MinMaxScaler
import matplotlib.pyplot as plt
Для этого проекта мы используем три пакета. NumPy будет служить для создания векторов и матриц, а также математических операций. Scikit-learn возьмет на себя обязанность по масштабированию данных, а Matpotlib предоставит график изменения показателей ошибки в процессе обучения сети.
Шаг 2: создание обучающей и контрольной выборок
Нейронные сети отлично справляются с изучением тенденций как в больших, так и в малых датасетах. Тем не менее специалисты по данным должны иметь в виду опасность возможного переобучения, которое чаще встречается в проектах с небольшими наборами данных. Переобучение происходит, когда алгоритм слишком долго обучается на датасете, в результате чего модель просто запоминает представленные данные, давая хорошие результаты конкретно на используемой обучающей выборке. При этом она существенно хуже обобщается на новые данные, а ведь именно это нам от нее и нужно.
Чтобы гарантировать оценку модели с позиции ее возможности прогнозировать именно новые точки данных, принято разделять датасеты на обучающую и контрольную выборки (а иногда еще и на тестовую).
input_train = np.array([[0, 1, 0], [0, 1, 1], [0, 0, 0],
[10, 0, 0], [10, 1, 1], [10, 0, 1]])
output_train = np.array([[0], [0], [0], [1], [1], [1]])
input_pred = np.array([1, 1, 0])
input_test = np.array([[1, 1, 1], [10, 0, 1], [0, 1, 10],
[10, 1, 10], [0, 0, 0], [0, 1, 1]])
output_test = np.array([[0], [1], [0], [1], [0], [0]])В этой простой нейронной сети мы будем классифицировать вектора 1х3 с 10 в качестве первого элемента. Вход и выход обучающей и контрольной выборок создаются с помощью функции NumPy array, а input_pred реализуется для тестирования функции prediction, которую мы определим позже. И обучающая, и контрольная выборки состоят из шести образцов с тремя признаками каждый. И поскольку выход определен заранее, этот пример можно считать обучением с учителем.
Шаг 3: масштабирование данных
Многие модели МО не способны понимать различия между, например единицами измерения, и будут, естественно, придавать большие веса признакам с большими величинами. Это может нарушить способность алгоритма правильно прогнозировать новые точки данных. Более того, обучение моделей МО на признаках с высокими величинами будет медленнее, чем нужно, по крайней мере при использовании градиентного спуска. Причина в том, что градиентный спуск сходится к искомой точке быстрее, когда значения находятся приблизительно в одном диапазоне.
scaler = MinMaxScaler()
input_train_scaled = scaler.fit_transform(input_train)
output_train_scaled = scaler.fit_transform(output_train)
input_test_scaled = scaler.fit_transform(input_test)
output_test_scaled = scaler.fit_transform(output_test)В наших обучающей и контрольной выборках значения расположены в относительно небольшом диапазоне, поэтому можно и не применять масштабирование признаков. Однако данная процедура все-таки включена, чтобы вы могли использовать собственные числа без особых изменений кода. Масштабирование признаков реализуется в Python очень легко, в чем помогает пакет Scikit-learn и его класс MinMaxScaler. Просто создайте объект MinMaxScaler и используйте функцию fit_transform с исходными данными в качестве входа. В результате эта функция вернет те же данные уже в масштабированном виде. В названном пакете есть и другие функции масштабирования, которые стоит попробовать.
Шаг 4: Создание класса нейронной сети
Один из простейших способов познакомиться со всеми элементами нейронной сети — создать соответствующий класс. Он должен включать все переменные и функции, которые потребуются для должной работы нейронной сети.
class NeuralNetwork():
def __init__(self, ):
self.inputSize = 3
self.outputSize = 1
self.hiddenSize = 3
self.W1 = np.random.rand(self.inputSize, self.hiddenSize)
self.W2 = np.random.rand(self.hiddenSize, self.outputSize)
self.error_list = []
self.limit = 0.5
self.true_positives = 0
self.false_positives = 0
self.true_negatives = 0
self.false_negatives = 0
def forward(self, X):
self.z = np.matmul(X, self.W1)
self.z2 = self.sigmoid(self.z)
self.z3 = np.matmul(self.z2, self.W2)
o = self.sigmoid(self.z3)
return o
def sigmoid(self, s):
return 1 / (1 + np.exp(-s))
def sigmoidPrime(self, s):
return s * (1 - s)
def backward(self, X, y, o):
self.o_error = y - o
self.o_delta = self.o_error * self.sigmoidPrime(o)
self.z2_error = np.matmul(self.o_delta,
np.matrix.transpose(self.W2))
self.z2_delta = self.z2_error * self.sigmoidPrime(self.z2)
self.W1 += np.matmul(np.matrix.transpose(X), self.z2_delta)
self.W2 += np.matmul(np.matrix.transpose(self.z2),
self.o_delta)
def train(self, X, y, epochs):
for epoch in range(epochs):
o = self.forward(X)
self.backward(X, y, o)
self.error_list.append(np.abs(self.o_error).mean())
def predict(self, x_predicted):
return self.forward(x_predicted).item()
def view_error_development(self):
plt.plot(range(len(self.error_list)), self.error_list)
plt.title('Mean Sum Squared Loss')
plt.xlabel('Epoch')
plt.ylabel('Loss')
def test_evaluation(self, input_test, output_test):
for i, test_element in enumerate(input_test):
if self.predict(test_element) > self.limit and \
output_test[i] == 1:
self.true_positives += 1
if self.predict(test_element) < self.limit and \
output_test[i] == 1:
self.false_negatives += 1
if self.predict(test_element) > self.limit and \
output_test[i] == 0:
self.false_positives += 1
if self.predict(test_element) < self.limit and \
output_test[i] == 0:
self.true_negatives += 1
print('True positives: ', self.true_positives,
'\nTrue negatives: ', self.true_negatives,
'\nFalse positives: ', self.false_positives,
'\nFalse negatives: ', self.false_negatives,
'\nAccuracy: ',
(self.true_positives + self.true_negatives) /
(self.true_positives + self.true_negatives +
self.false_positives + self.false_negatives))Шаг 4.1: создание функции инициализации
Функция _init_ вызывается при создании класса, что позволяет правильно инициализировать его переменные.

def __init__(self, ):
self.inputSize = 3
self.outputSize = 1
self.hiddenSize = 3
self.W1 = torch.randn(self.inputSize, self.hiddenSize)
self.W2 = torch.randn(self.hiddenSize, self.outputSize)
self.error_list = []
self.limit = 0.5
self.true_positives = 0
self.false_positives = 0
self.true_negatives = 0
self.false_negatives = 0
В этом примере я выбрал нейронную сеть с тремя входными узлами, тремя узлами в скрытом слое и одним выходным узлом. Вышеприведенная функция _init_ инициализирует переменные, описывающие размер нейронной сети. inputSize — это количество входных узлов, которое должно равняться количеству признаков во входных данных. outputSize равна числу выходных узлов, а hiddenSize указывает их количество в скрытом слое. Кроме того, между узлами сети будут также присутствовать веса, подстраиваемые в процессе обучения.
В дополнение к переменным, описывающим размер нейронной сети и ее веса, я создал несколько переменных, инициализируемых при создании объекта NeuralNetwork, который будет использован для оценки эффективности сети. error_list будет содержать среднюю абсолютную ошибку (MAE) для каждой эпохи, а ее порог будет указывать границу, определяющую должен ли вектор классифицироваться как содержащий или не содержащий в начале элемент 10. Затем идут переменные, которые будут служить для хранения количества верных положительных и ложных положительных, а также верных отрицательных и ложных отрицательных результатов.
Шаг 4.2: создание функции прямого распространения
Цель этой функции в прямом проходе через все слои нейронной сети и прогнозировании выхода для каждой эпохи. После этого на основе разницы между спрогнозированным выходом и фактическими данными в процессе обратного распространения происходит обновление весов.
def forward(self, X):
self.z = np.matmul(X, self.W1)
self.z2 = self.sigmoid(self.z)
self.z3 = np.matmul(self.z2, self.W2)
o = self.sigmoid(self.z3)
return oДля вычисления значений узлов каждого слоя выполняется операция матричного умножения значений узлов предыдущего слоя на соответствующие веса, после чего применяется нелинейная функция активации для расширения вероятностей конечной выходной функции. В данном примере я выбрал в качестве функции активации сигмоиду, но есть и другие альтернативы.
Шаг 4.3: создание функции обратного распространения ошибки
Обратное распространение ошибки — это процесс обновления весов узлов нейронной сети, определяющий их важность.
def backward(self, X, y, o):
self.o_error = y - o
self.o_delta = self.o_error * self.sigmoidPrime(o)
self.z2_error = np.matmul(self.o_delta,
np.matrix.transpose(self.W2))
self.z2_delta = self.z2_error * self.sigmoidPrime(self.z2)
self.W1 += np.matmul(np.matrix.transpose(X), self.z2_delta)
self.W2 += np.matmul(np.matrix.transpose(self.z2),
self.o_delta)В приведенном фрагменте кода итоговая ошибка выходного слоя вычисляется как разность между спрогнозированным выходом, полученным в ходе прямого распространения, и фактическим выходом. Затем эта ошибка умножается на сигмоиду для выполнения градиентного спуска, после чего весь процесс повторяется, пока не будет достигнут входной слой. В завершении веса между слоями обновляются.
Шаг 4.4: создание функции обучения
В процессе обучения алгоритм выполняет прямой и обратный проход, обновляя веса столько раз, сколько будет пройдено эпох. Это необходимо, чтобы в итоге получить наиболее точные их значения.
def train(self, X, y, epochs):
for epoch in range(epochs):
o = self.forward(X)
self.backward(X, y, o)
self.error_list.append(np.abs(self.o_error).mean())Помимо выполнения прямого и обратного прохода мы сохраняем среднюю абсолютную ошибку (MAE) в списке, чтобы потом можно было проследить ее изменение в ходе обучения.
Шаг 4.5: создание функции прогнозирования
После тонкой настройки весов алгоритм готов прогнозировать выход для новых точек данных. Это выполняется одной итерацией прямого прохода. Спрогнозированный выход будет числом, которое, как мы надеемся, окажется близко к фактическому выходу.
def predict(self, x_predicted):
return self.forward(x_predicted).item()
Шаг 4.6: построение графика изменения MAE
Для оценки качества алгоритма МО есть много способов. Зачастую для этого используется средняя абсолютная ошибка, что позволяет уменьшить число эпох обучения.
def view_error_development(self):
plt.plot(range(len(self.error_list)), self.error_list)
plt.title('Mean Sum Squared Loss')
plt.xlabel('Epoch')
plt.ylabel('Loss')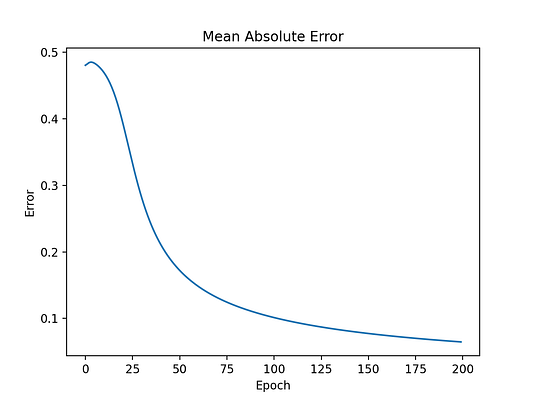
Шаг 4.7: вычисление точности и ее компонентов
Количество верных положительных, верных отрицательных и ложных положительных результатов описывает качество алгоритма классификации. После обучения нейронной сети веса должны быть обновлены так, чтобы этот алгоритм мог точно прогнозировать новые точки данных. В задачах двоичной классификации этими точками могут быть только 1 или 0. В зависимости от того, находится спрогнозированное значение выше или ниже определенного порога, алгоритм классифицирует запись как 1 или 0.
def test_evaluation(self, input_test, output_test):
for i, test_element in enumerate(input_test):
if self.predict(test_element) > self.limit and \
output_test[i] == 1:
self.true_positives += 1
if self.predict(test_element) < self.limit and \
output_test[i] == 1:
self.false_negatives += 1
if self.predict(test_element) > self.limit and \
output_test[i] == 0:
self.false_positives += 1
if self.predict(test_element) < self.limit and \
output_test[i] == 0:
self.true_negatives += 1
print('True positives: ', self.true_positives,
'\nTrue negatives: ', self.true_negatives,
'\nFalse positives: ', self.false_positives,
'\nFalse negatives: ', self.false_negatives,
'\nAccuracy: ',
(self.true_positives + self.true_negatives) /
(self.true_positives + self.true_negatives +
self.false_positives + self.false_negatives))При выполнении функции test_evaluation получаем следующие результаты:
Верные положительные: 2
Верные отрицательные: 4
Ложные положительные: 0
Ложные отрицательные: 0
Точность задается этой формулой:
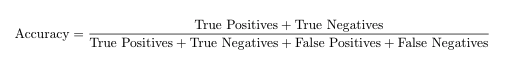
Исходя из результатов, можно сделать вывод, что в нашем случае точность равна 1.
Шаг 5: выполнение скрипта, обучающего и оценивающего модель нейронной сети
NN = NeuralNetwork()
NN.train(input_train_scaled, output_train_scaled, 200)
NN.predict(input_pred)
NN.view_error_development()
NN.test_evaluation(input_test_scaled, output_test_scaled)Чтобы испытать наш класс нейронной сети, мы начнем с инициализации объекта типа NeuralNetwork. После этого сеть в течение 200 эпох обучается на обучающей выборке для тонкой настройки весов. Затем итоговая модель тестируется на контрольном векторе. После этого графически отображается изменение ошибки, и модель оценивается на контрольной выборке.
Весь проект и его код можете найти на GitHub.
Шаг 6: доработка скрипта и экспериментирование
Представленный код можно легко изменить для обработки и других аналогичных ситуаций. Рекомендую вам поэкспериментировать с ним, изменив переменные и использовав собственные данные. Среди возможных идей по оптимизации можете рассмотреть:
- Обобщение кода для работы с данными, имеющими любой входной и выходной размер.
- Отслеживание изменения эффективности алгоритма не с помощью средней абсолютной ошибки, а другой метрики.
- Применение иной функции масштабирования.
Читайте также:
- Лучший алгоритм решения задач по программированию на Python
- 80 практических вопросов по Python для собеседования
- Насколько С++ быстрее Python
Читайте нас в Telegram, VK и Яндекс.Дзен
Перевод статьи Chris Verdence: How to Create a Simple Neural Network in Python






