Примеры из веб-приложения здесь.
Зачем
В 1959 году Эдсгер Дейкстра пришел к выводу о том, что компьютеры могут находить самые эффективные траектории, измеряя и высчитывая расстояния в графе. Алгоритм этот крайне важен, хотя бы потому, что определение кратчайшего пути помогает туристам выстраивать наиболее «вместительные» маршруты.
Данная концепция до сих пор активно используется во многих приложениях для отрисовки маршрутов на картах.
Что
Начнем с развития интуитивного определения кратчайшего маршрута.
Определим кратчайший путь из SD.
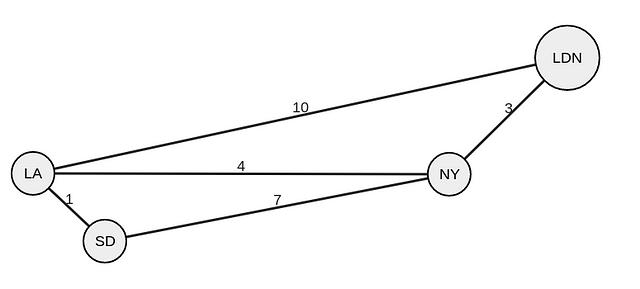
Первым делом создаем наборы данных visited («посещено») и distance («расстояние»). Установим их значения на false («ложь») и infinity («бесконечность»).
Обновим расстояние в начальном узле SD до нуля и назовем его «текущим» узлом.
visited = {SD: false, LA: false, NY: false, LDN: false}
distance = {SD: 0, LA: INT_MAX, NY: INT_MAX, LDN: INT_MAX}

Теперь вычислим расстояние между текущим узлом и соседними. Если предварительное расстояние меньше фактического, то обновляем расстояние.
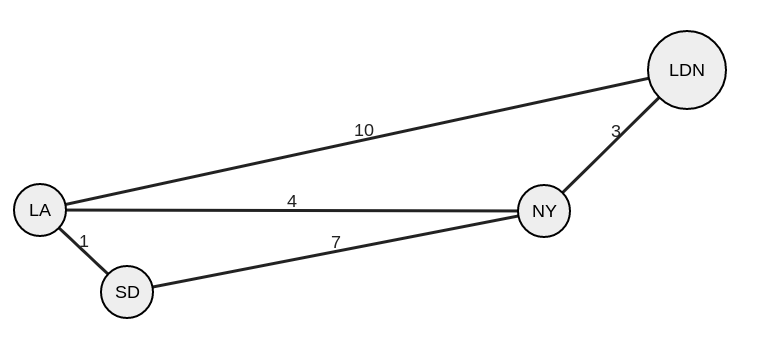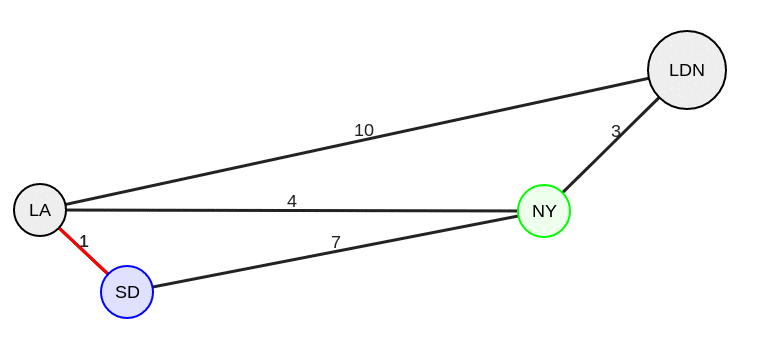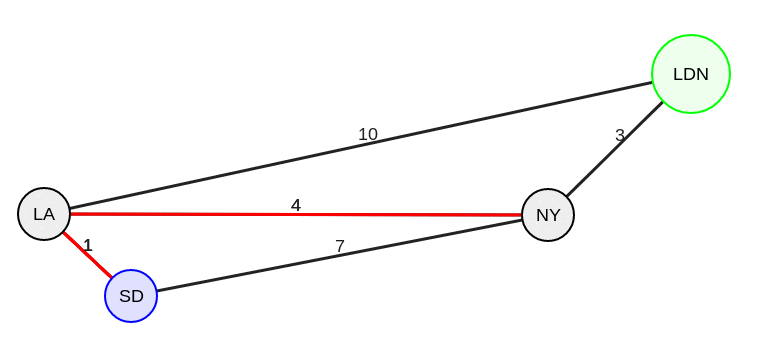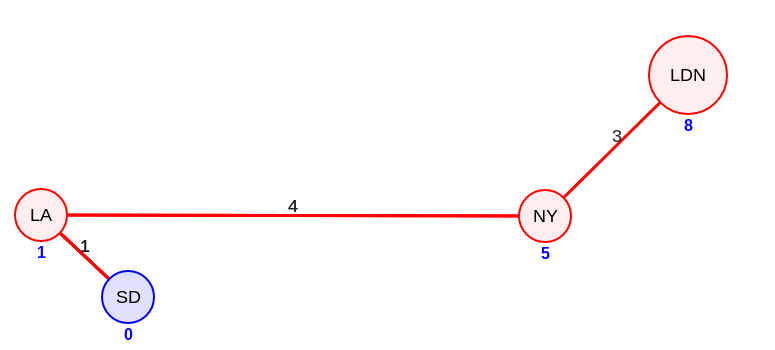
Расстояние от SD до LA (0+1) меньше бесконечности. Поэтому расстояние в LA обновляется до одного. Расстояние SD-NY = 0+7. Это также меньше бесконечности. Поэтому расстояние в NY обновляется до семи. LDN не связано напрямую с SD, поэтому расстояние в LDN остается бесконечным.
Завершим итерацию обновлением значения «посещено» в SD на true («истина»).
visited = {SD: true, LA: false, NY: false, LDN: false}
distance = {SD: 0, LA: 1, NY: 7, LDN: INT_MAX}
Следующую итерацию начнем с выбора нового текущего узла — с самым маленьким значением расстояния и false в посещено. Тогда текущим узлом станет LA — расстояние «один», к посещенным не относится.
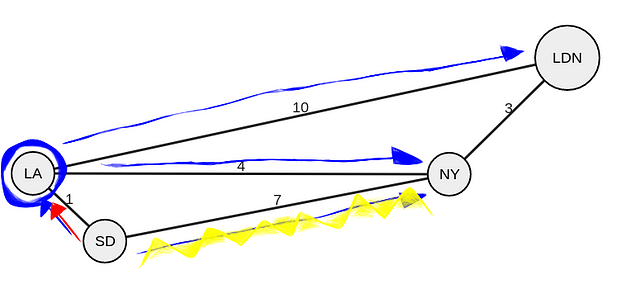
Вновь рассчитаем расстояние из текущего узла (LA) до соседних, и если предварительное расстояние меньше фактического, то обновим значение.
Вы заметили, что расстояние от LA до NY (1+4) меньше текущего фактического расстояния (7)? Это означает, что был найден более короткий путь. Теперь в точку NY можно попасть из SD с расстоянием пять, проходя через LA.
Расстояние LA-LDN (1+10) меньше бесконечности, поэтому в LDN можно попасть, пройдя расстояние в одиннадцать.
Закончим итерацию, обновив значение посещено в LA на true.
visited = {SD: true, LA: true, NY: false, LDN: false}
distance = {SD: 0, LA: 1, NY: 5, LDN: 11}
Следующая итерация выделяет узел с самым маленьким значением в расстоянии, которое, к тому же должно не относиться к посещенным. И в данном случае текущим узлом будет выбран NY.
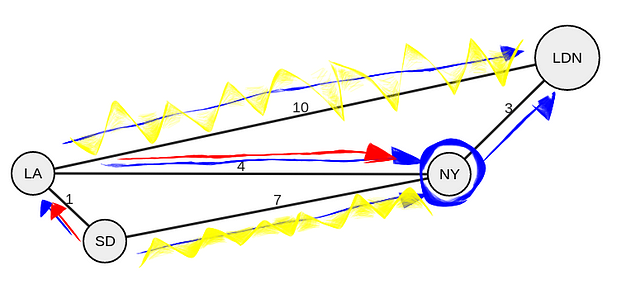
Еще один раз просчитаем расстояния между NY и соседними узлами. И обновим расстояние, если предварительное окажется меньше фактического.
Находится кратчайший путь из NY в LDN: 5+3 — это меньше, чем фактическое значение 11, так что обновляем расстояния в LDN до восьми.
visited = {SD: true, LA: true, NY: true, LDN: false}
distance = {SD: 0, LA: 1, NY: 5, LDN: 8}
Заканчиваем итерацию присвоением посещено в NY значения true.
visited = {SD: true, LA: true, NY: true, LDN: false}
distance = {SD: 0, LA: 1, NY: 5, LDN: 8}
Выбираем следующий не посещенный узел с наименьшим расстоянием — LDN.

Новых маршрутов для посещения больше нет. Все доступные узлы были посещены, так что алгоритм считается завершенным.
visited = {SD: true, LA: true, NY: true, LDN: true}
distance = {SD: 0, LA: 1, NY: 5, LDN: 8}
10 шагов для написания кода алгоритма Дейкстры:
1. Создаем набор данных посещено для всех узлов графа.
2. Создаем набор данных расстояние для всех узлов графа.
3. Присваиваем посещено значение false (не посещено), а расстояние делаем равным бесконечности (недостижимо).
4. Выбираем начальный узел и присваиваем расстоянию этого узла значение ноль.
5. В первой итерации начальным узлом будет текущий узел.
6. Теперь текущий узел прокладывает путь до всех соседних узлов и просчитывает предварительное расстояние.
7. Предварительное расстояние — это путь от текущего узла до грани соседнего узла.
8. Если предварительное расстояние меньше заданного, то расстояние обновляется.
9. Меняем текущий узел, задавая значение true в посещено.
10. Выбираем следующий текущий узел с наименьшим расстоянием и значением false в посещено.
11.Повторяем шаги 6–9 то тех пор, пока все узлы не окажутся посещенными, или во всех оставшихся не посещенных узлах расстояние не изменится на бесконечность (недостижимо).
Как
А теперь давайте посмотрим на выполнение алгоритма в коде.
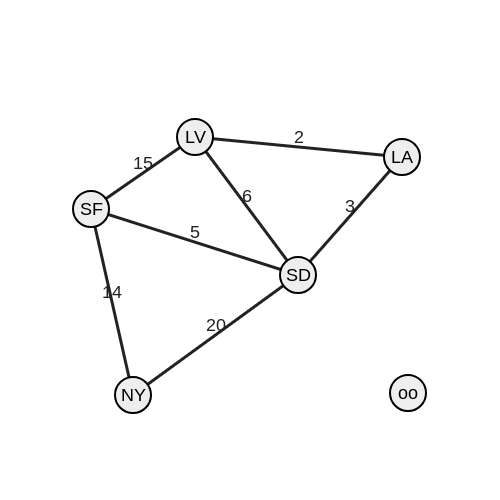
Граф можно представить в виде рисунка ниже (круглые узлы, прямые грани) или в форме массива массивов.
Если выбрать представление в виде массивов, то каждый индекс будет обозначать узел, а каждое значение — его грань. Например, код arr[0][1] = 3; можно будет прочесть, как «из узла 0 в узел 1 с гранью 3».
Таким образом, сама картинка (слева) и код (справа) представляют собой один и тот же граф.
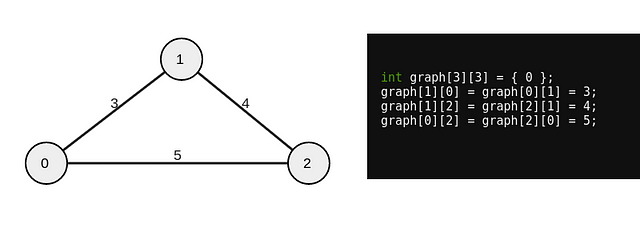
Каждый из этих графов содержит 3 узла и 3 грани: 0–1 с гранью 3, 1–2 с гранью 4 и 2–0 с гранью 5.
Обратите внимание, что массивы описывают только направленные грани, а зеркальные индексы имеют те же самые значения, благодаря чему каждая грань становится многонаправленной. То есть, graph[0][1] = graph[1][0] = 3. Если есть путь от узла 0 к узлу 1, то есть и обратный путь, соединяющий 1 и 0.
А теперь сам алгоритм.
Алгоритм Дейкстры:
void dijkstrasAlgorithm(int graph[SIZE][SIZE], int cur) {
//создаем массивы "расстояние" и "посещено"//
int distance[SIZE];
bool visited[SIZE];
//присваиваем следующие значения: расстояние = "бесконечность", посещено = "не посещено"//
for(int i=0; i<SIZE; i++)
distance[i] = INT_MAX, visited[i] = false;
//в начальном узле ставим расстояние равным нулю//
distance[cur] = 0;
//выполняем нужное количество итераций, пока узел достижим и не посещен//
while(cur!=-1) {
//для соседних узлов сравниваем предварительное и заданное расстояние//
for(int i=0; i<SIZE; i++)
if((graph[cur][i]+distance[cur]<distance[i])&&graph[cur][i])
distance[i] = graph[cur][i]+distance[cur];
//отмечаем текущий узел "посещенным" и выбираем следующий//
visited[cur] = true, cur = -1;
int mindistance = INT_MAX;
for(int i=0; i<SIZE; i++)
if(!visited[i] && (distance[i] < mindistance))
cur = i, mindistance = distance[i];
}
}
Алгоритм создает массивы для расстояния и посещено. Эти массивы обозначаются как SIZE . Затем массивам присваиваются INT_MAX и false, для недостижимого и не посещенного соответственно.
Далее расстояние в начальном, текущем, узле приравнивается к нулю.
Текущий узел высчитывает предварительное расстояние. Если оно меньше заданного, то расстояние обновляется.
Например, в if((graph[cur][i]+distance[cur]) < distance[i]) && graph[cur][i]) расстояние будет обновляться.
Теперь завершим итерацию, изменив посещено для текущего узла на true и обновив значение текущего узла на отрицательное (null).
Поищем новый текущий узел. По требованиям алгоритма этот узел должен быть достижимым (расстояние меньше INT_MAX) и не посещенным (значение false в массиве «посещено»).
Через какое-то время все узлы окажутся либо посещенными, либо отмеченными в качестве недостижимых и не посещенных. В любом случае, алгоритм завершится при достижении отрицательного значения в текущем узле.
12. Копируем код в текстовый редактор и сохраняем под именем main.cpp
13. Компилируем код с командной строки, g++ main.cpp -o Dijkstra.exe
14. Выполняем код с командной строки, ./Dijkstra.exe
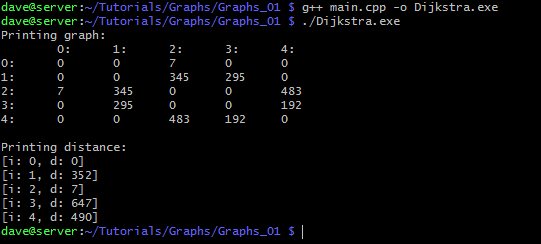
После компиляции и выполнения исходного кода программа отрисовывает произвольный граф и находит нужные траектории по алгоритму Дейкстры.
Если все шаги были выполнены верно, то на выходе вы получите похожий результат.
Результат
Код
Просмотреть код С++ полностью можно здесь.
Перевод статьи David Pynes: Graphs & paths: Dijkstra





