Обучение единой универсальной модели для решения произвольных наборов данных всегда было мечтой исследователей в области машинного обучения, особенно в эпоху базовых моделей. Хотя эти мечты уже осуществились в области восприятия, такой как изображения или естественные языки, остается открытой проблемой то, можно ли их воспроизвести в области рассуждений, например в графах.
В этой публикации авторы доказывают, что существует универсальная модель рассуждения, по крайней мере, для графов знаний (KG). Так была создана ULTRA — единственная предварительно обученная модель рассуждения, которая обобщается на новые графы знаний с произвольными сущностями и словарями отношений. Такая модель служит в качестве стандартного решения для любой задачи формирования рассуждений в KG.
Почему обучение представлений графов знаний застряло в 2018 году?
Парадигма предварительного обучения и дообучения существует с 2018 года, когда модели ELMo и ULMFit показали первые многообещающие результаты, а позже были укреплены моделями BERT и GPT.
В эпоху больших языковых моделей (LLM) и более общих базовых моделей (FMs), мы часто имеем одну модель (например, GPT-4 или Llama-2), предварительно обученную на огромном объеме данных и способную выполнять широкий спектр языковых задач в режиме “нулевого обучения” (или по крайней мере быть дообученной на конкретных наборах данных). В наши дни мультимодальные базовые модели даже поддерживают текст, изображения, видео, аудио и другие модальности в рамках одной модели.
В Graph ML (машинном обучении на графах) все происходит немного по-другому. В частности, что происходит с обучением представлений данных на графах к концу 2023 года? Основные задачи здесь связаны с уровнем ребра:
- Entity prediction (предсказание сущностей или завершение графов знаний) (h,r,?): дан начальный узел и отношение, необходимо упорядочить все узлы в графе, которые могут быть потенциально истинными конечными узлами.
- Prediction of relation (предсказание отношения) (h,?,t): даны два узла, нужно предсказать тип отношения между ними.
Оказывается, до сих пор это было где-то до 2018 года. Основная проблема заключается в том, что:
У каждого графа знаний есть свой набор сущностей и отношений, и нет единой предварительно обученной модели, которая бы могла быть применима для любого графа.
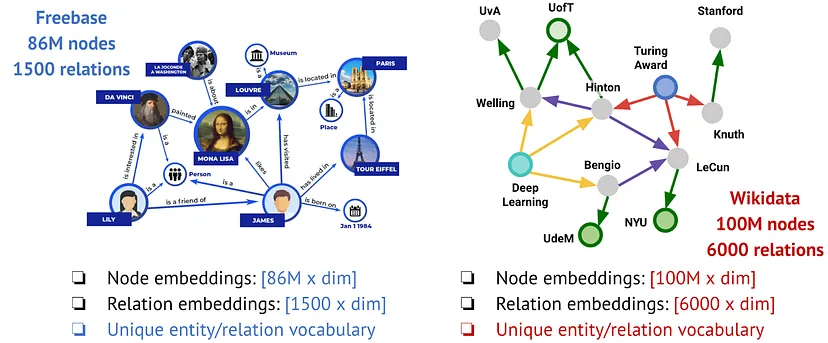
Например, если мы рассмотрим Freebase (граф знаний, лежащий в основе графа знаний Google) и Wikidata (самый большой общедоступный граф знаний), то они имеют абсолютно разные наборы сущностей (86 миллионов против 100 миллионов) и отношений (1 500 против 6 000). Есть ли хоть какая-то надежда, что текущие методы обучения представлений графов знаний могут быть обучены на одном графе и применены к другому?
Классические трансдуктивные методы, такие как TransE, ComplEx, RotatE и сотни других методов, основанных на вложениях, изучают фиксированный набор сущностей и типов отношений на графе обучения и даже не могут поддерживать новые узлы, добавленные в тот же граф. Ограниченные методы, основанные на вложениях, не переносятся (мы считаем, что нет смысла разрабатывать такие методы, кроме как для некоторых учебных проектных упражнений).
Методы индуктивной сущности, такие как NodePiece и Neural Bellman-Ford Nets, не обучают векторы сущности. Вместо этого они параметризуют обучающие узлы (наблюдаемые) и новые узлы вывода (ненаблюдаемые) как функцию фиксированных отношений. Поскольку они обучают только векторы отношений, это позволяет им переноситься на графы с новыми узлами, но перенос на новые графы с разными отношениями (например, из Freebase в Wikidata) все еще выходит за пределы их возможностей.
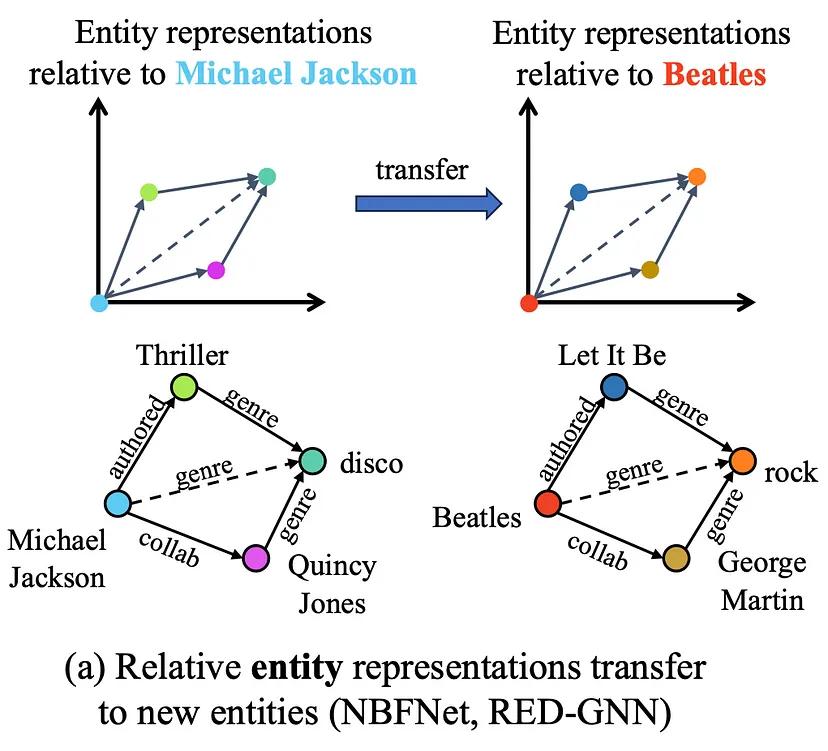
Что делать, если у вас есть и новые сущности, и отношения во время вывода (совершенно новый граф)? Если вы не обучали векторы сущностей или отношений, то теоретически возможен ли такой перенос? Разберемся в теории.
Теория: что делает модель индуктивной и переносимой?
Определим настройки более формально.
- Графы знаний являются направленными, мультиреляционными графами со случайным набором узлов и типов отношений.
- Графы представлены без свойств, то есть мы не предполагаем наличие текстовых описаний (или предварительно вычисленных векторов свойств) сущностей и отношений.
- Учитывая запрос (head, relation, ?), необходимо ранжировать все узлы в основном графе (граф вывода) и максимизировать вероятность возврата истинного хвоста.
- Трансдуктивная настройка: набор узлов и сущностей одинаков во время обучения и вывода.
- Индуктивная настройка (сущность): набор отношений должен быть фиксирован во время обучения, но узлы могут изменяться при обучении и выводе.
- Индуктивная настройка (сущность и отношение): новые и ранее невиданные сущности и отношения разрешены при выводе.
Что изучают нейронные сети для того, чтобы обобщать новые данные? Основное утверждение, приведенное в книге “Geometric Deep Learning” Бронштейна, Бруны, Коэна и Величковича, гласит, что это вопрос симметрий и инвариантностей.
Какие инварианты допускают обучение в базовых моделях? Большие языковые модели обучаются на фиксированном словаре токенов (подсловных единиц, байтов или даже случайно инициализированных векторов, как в моделях Lexinvariant), модели обработки видеоизображений обучаются функциям для проектирования областей изображения, а аудиомодели обучаются проектированию аудиофрагментов.
Какие существуют обучаемые инварианты для мультиреляционных моделей?
Сначала мы рассмотрим инварианты (эквиварианты) в стандартных однородных графах.
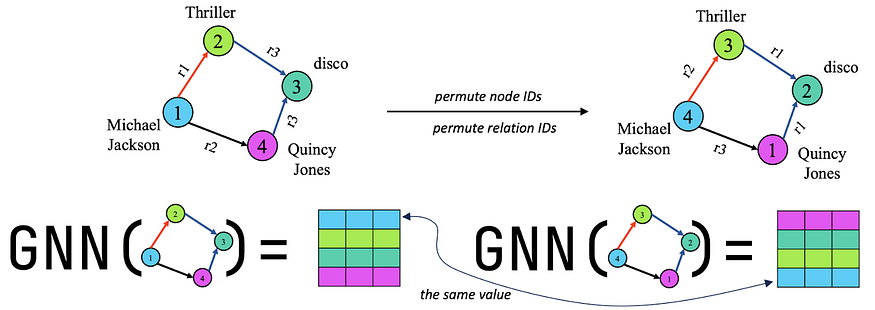
Стандартные (одиночные) перестановочные графовые модели. Большой прорыв в графовом машинном обучении произошел, когда ранние работы по графовым нейронным сетям показали, что индуктивные задачи на графах получают огромную пользу от предположения о произвольности идентификаторов вершин, то есть прогнозы графовой модели не должны изменяться, если мы переназначим идентификаторы вершин. Речь идет о перестановочной эквивариантности нейронной сети по идентификаторам узлов. Такое достижение вызвало большой восторг и множество новых методов представления графов, поскольку, пока нейронная сеть эквивариантна к перестановке идентификаторов узлов, мы можем называть ее графовой моделью.
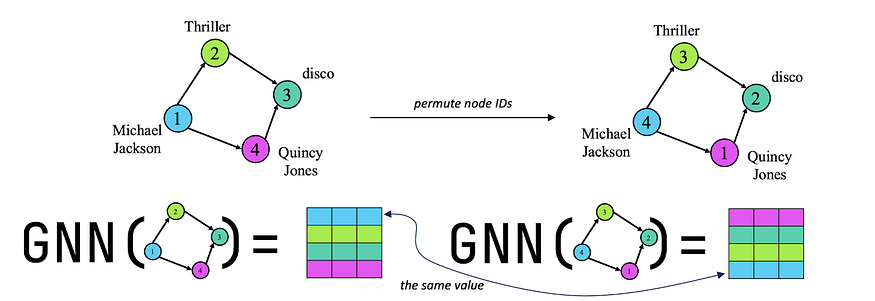
Перестановочная эквивариантность по идентификаторам вершин позволяет графовым нейронным сетям индуктивно (на нулевом уровне) передавать образцы, изученные на тренировочном графе, на другой (отличающийся) тестовый граф. Это является следствием эквивариантности, так как нейронная сеть не может использовать идентификаторы вершин для создания вложений, она должна использовать структуру графа. Таким образом создается то, что нам знакомо как структурные представления на графах (см. Srinivasan & Ribeiro (ICLR 2020)).
Эквивариантность в мультиреляционных графах
Существует ли теория графовых нейронных сетей для таких графов, в которых ребра могут иметь различные типы связей?
- Существует так называемая Relational WL — иерархия выразительности графового языка WL (Weisfeiler-Lehman) для мультиреляционных графов, которая сосредоточена на задачах на уровне узлов. Согласно теории предсказания связей, с помощью Relational WL можно сформировать условные передачи сообщений и логическую выразительность. Благодаря условной передачи сообщений повышается производительность предсказания связей.
- Графовые модели двойной перестановочной эквивариантности (мультиреляционные). Недавно была предложена концепция двойной эквивариантности для мультиреляционных графов. Благодаря двойной эквивариантности нейронная сеть становится эквивариантной к совместным перестановкам, как идентификаторов узлов, так и идентификаторов отношений. Это гарантирует, что нейронная сеть будет изучать структурные закономерности между узлами и отношениями, что позволит ей индуктивно (на нулевом уровне) передавать изученные закономерности в другой граф с новыми узлами и новыми отношениями.
В этой работе была обнаружена инвариантность взаимодействий между отношениями, то есть, даже если идентификаторы отношений различаются, их фундаментальные взаимодействия остаются неизменными, и эти фундаментальные взаимодействия могут быть описаны графом отношений. В графе отношений каждый узел представляет собой тип отношения из исходного графа. Два узла в этом графе будут соединены, если ребра с этими типами отношений в исходном графе инцидентны (то есть они имеют общий начальный или конечный узел). В зависимости от инцидентности мы различаем 4 типа ребер в графе отношений.
- Head-to-head (h2h) — две связи могут начинаться от одной и той же исходной сущности.
- Tail-to-head (t2h) — конечная сущность одной связи может стать исходной сущностью другой связи.
- Head-to-tail (h2t) — исходная сущность одной связи может стать конечной сущностью другой связи.
- Tail-to-tail (t2t) — две связи могут иметь одну и ту же конечную сущность.
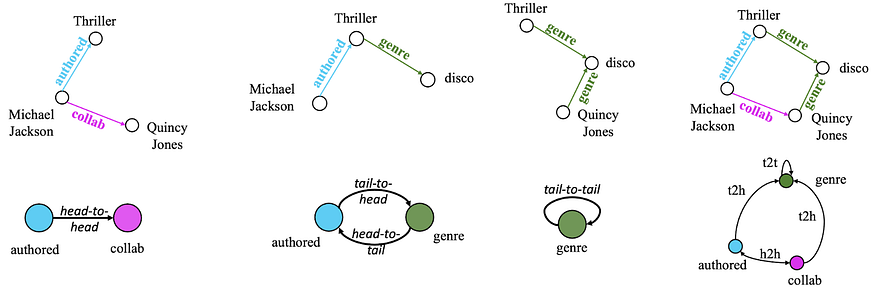
Парочка прекрасных свойств реляционного графа:
- Он может быть образован от абсолютно любого мультиреляционного графа (с помощью простого умножения разреженных матриц).
- 4 основных взаимодействия никогда не меняются, потому что они закодированы в основной топологии — в ориентированных графах всегда будут существовать исходные и конечные вершины, и отношения будут иметь такие паттерны инцидентности.
Фактически, изучение представлений на графе отношений может быть применено к любому мультиреляционному графу, поскольку является обучаемой инвариантностью.
Более того, можно показать, что представление отношений через их взаимодействия в графе отношений является двойной эквариантной моделью. Это означает, что изучаемые отношения независимы от их идентичности и, скорее, основаны на совместных взаимодействиях между отношениями и узлами.
ULTRA — базовая модель для формирования рассуждений с помощью графов знаний
ULTRA — это метод для унифицированного, обучаемого и переносимого представления графов. ULTRA использует инвариантность (и эквивариантность) графа отношений с его фундаментальными взаимодействиями и применяет условную передачу сообщений для получения относительных реляционных представлений. Возможно, самое крутое здесь то, что единственная предварительно обученная модель ULTRA может выполнять вывод при нулевой подготовке на любом возможном мультиреляционном графе и быть дообученной на любом графе.
Другими словами, ULTRA — это в основном базовая модель, которая может выполнять вывод на любом входном графе (с уже хорошей производительностью) и быть доведенной до совершенства на любом целевом графе, который нас интересует.
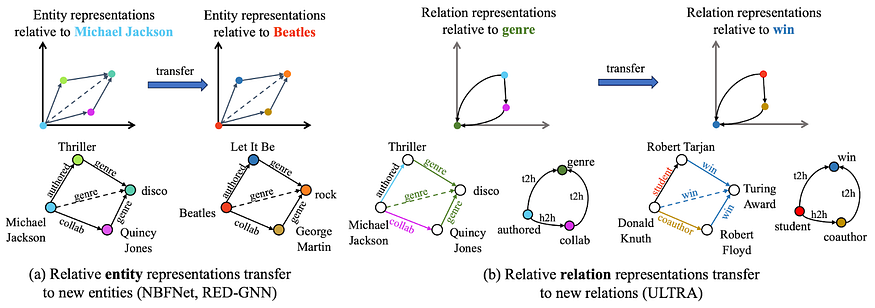
Ключевым компонентом ULTRA являются относительные представления отношений, создаваемые на основе графа отношений. Для заданного запроса (Майкл Джексон, жанр, ?) мы сначала инициализируем узел жанра в графе отношений вектором из всех единиц (все остальные узлы инициализируются нулями). После запуска GNN результирующие векторы узлов в графе отношений зависят от узла жанра — это означает, что каждый исходный инициализированный узел отношений будет иметь свою матрицу признаков отношений, и это очень полезно с точки зрения как теоретических, так и практических аспектов.
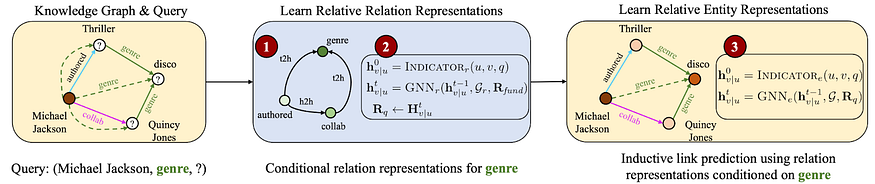
На практике при заданном входном графе знаний и запросе (h, r, ?) ULTRA выполняет следующие действия:
- Составляет граф отношений.
- Получает характеристики связи с помощью условного прохода сообщений GNN на графе связей (при условии инициализации запроса связи r).
- Использует полученные относительные представления для индуктивного предсказателя связи GNN при условии инициализированного начального узла h.
Шаги 2 и 3 реализуются с помощью немного отличных модификаций нейронной сети Neural Bellman-Ford (NBFNet). ULTRA учит только векторы 4 основных взаимодействий (h2t, t2t, t2h, h2h) и весы GNN — в целом довольно маленькие. Основная модель, которая была изучена, имеет всего 177 тысяч параметров.
Эксперименты: лучшие даже в нулевом размечевании и настройке модели
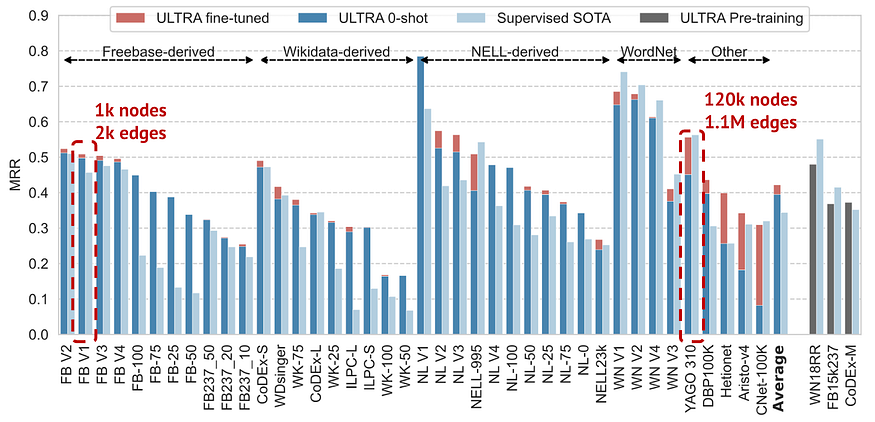
ULTRA (модель, предназначенную для работы с графами знаний) была предварительно обучена на 3 стандартных графах знаний, основанных на Freebase, Wikidata и Wordnet. Затем было проверено предсказание связей без использования обучающего набора на более чем 50 других графах знаний различного размера — от 1 тыс. до 120 тыс. узлов и от 2 тыс. до 1,1 млн ребер.
Усредненная по данным наборам с известными SOTA (самое передовое состояние), единая предварительно обученная модель ULTRA в режиме нулевой доработки работает лучше, чем существующие модели SOTA, обученные специально на каждом графе. Настройка модели улучшает производительность еще на 10% дополнительно. Особенно удивительно, что ULTRA может масштабироваться для графов с такими различными размерами (разница в размере узлов в 100 раз и в размере ребер в 500 раз), в то время как GNN страдают от проблем обобщения размера.
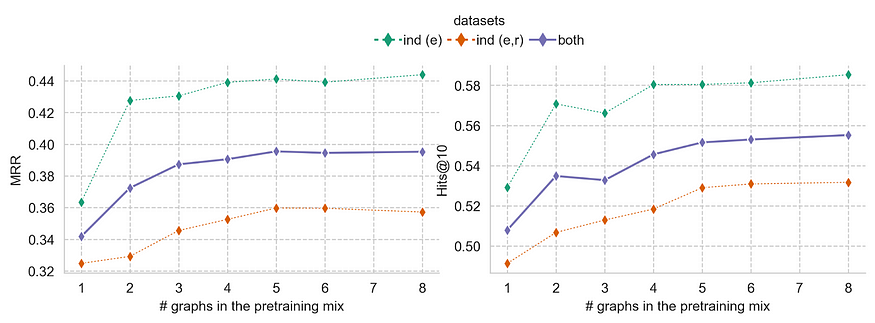
Поведение масштабирования
Мы можем улучшить производительность без дообучения еще больше, добавляя больше графов в предварительную подготовку, хотя мы наблюдаем определенное достижение предельной производительности после обучения на более чем 4 графах.
Законы масштабирования прогнозируют еще более высокую производительность с использованием больших моделей, обученных на качественных данных.
Заключение: код, данные, контрольные точки
Итак, мы преодолели порог 2018 года и получили базовые модели для формирования рассуждений с помощью графов знаний. Одна предварительно обученная модель ULTRA может выполнять предсказание связей на любом графе знаний (мультиреляционном графе) из любой области. Чтобы начать работу, нужен лишь граф с более чем 1 типом ребер.
На практике ULTRA уже показывает очень многообещающие результаты на различных тестах графов знаний даже без предварительного обучения. Однако вы можете добиться еще более высокой производительности после небольшой настройки модели.
Формирование рассуждений с помощью графов знаний представляет лишь часть множества интересных проблем в этой области, и большинство из них все еще не имеют общего решения. Тем не менее успех формирования рассуждений с помощью графов знаний приведет к новым прорывам в других областях рассуждения (например, использование текстовых правил в языковых моделях).
Читайте также:
- Как освоить машинное обучение
- Машинное обучение без данных
- Как выбрать язык программирования для проекта машинного обучения
Читайте нас в Telegram, VK и Дзен
Перевод статьи Michael Galkin: ULTRA: Foundation Models for Knowledge Graph Reasoning