Представляю метод решения популярной задачи по программированию. Созданная мной функция эффективно решает судоку с помощью хэш-карт и рекурсий. Думаю, что по мере совершенствования найду новые способы сделать это решение более эффективным и менее громоздким. А пока это первый рабочий проект.
Ниже я описал весь ход размышлений и привел код с пояснениями и комментариями.
Шаг 1. Определяем способ организации данных
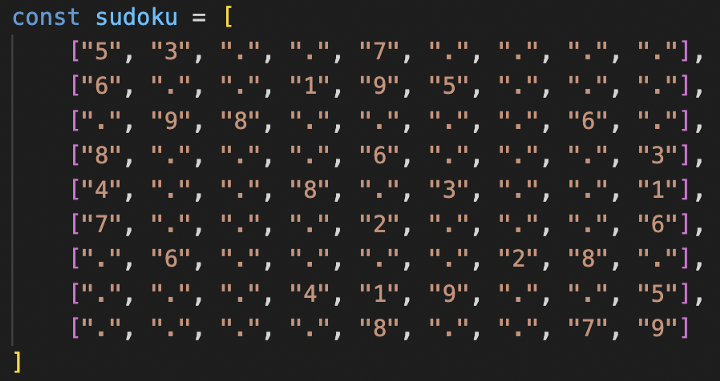
Подход заключается в том, чтобы рассматривать каждую строку, столбец и блок по отдельности. Это звучит как очевидный первый шаг, но на практике все оказывается сложнее.
Головоломка будет передана в виде одного массива, включающего 9 других массивов чисел. Проблема заключается в том, как повысить эффективность проверки каждого блока? Как сообщить коду, в каком блоке находится та или иная ячейка? При решении судоку нужно проверять не только каждую строку и столбец, но и каждый блок, чтобы убедиться, что определенное число встречается только раз.
Шаг 2. Упорядочиваем данные
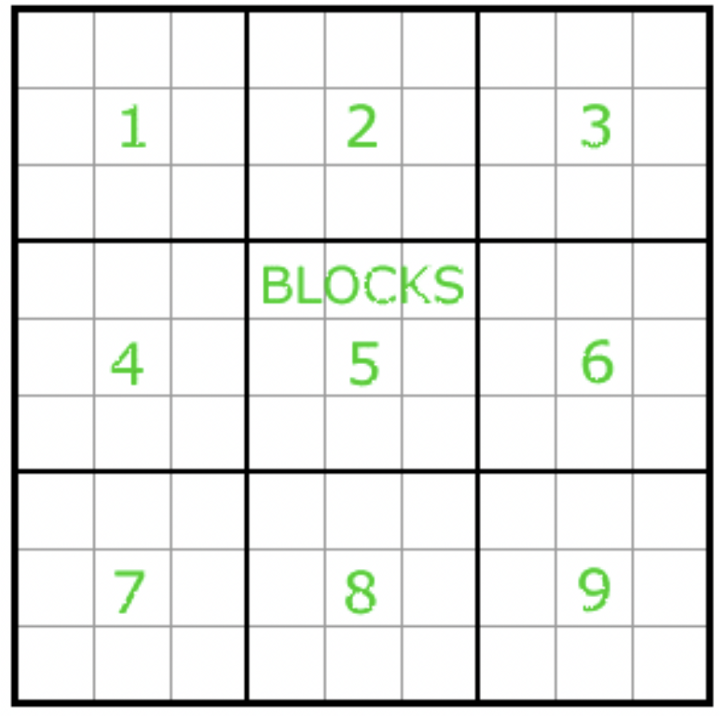
Я решил промаркировать каждый блок судоку от 1 до 9. Начинал с верхнего левого угла и двигался слева направо, а затем спускался ниже. Такой способ повторяет принцип чтения книги.
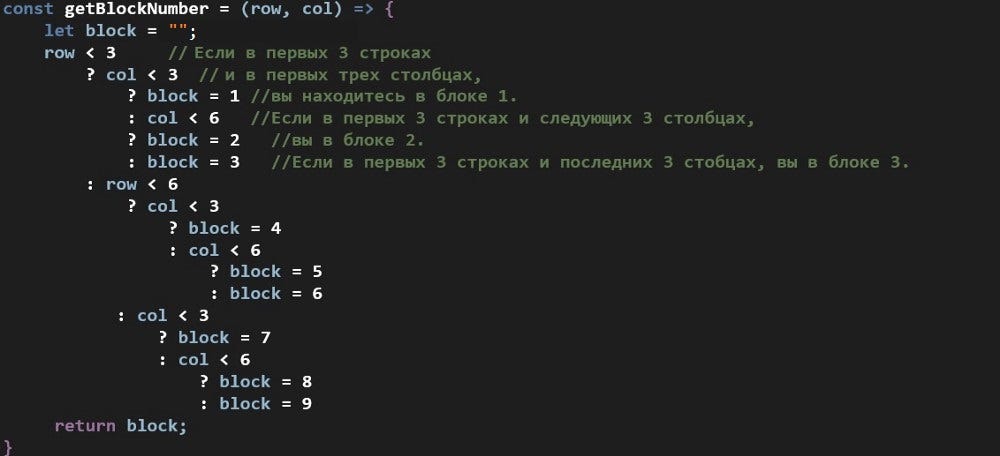
Блок приведенного выше кода я рассматриваю как шаг перед первым шагом. Эта функция принимает два параметра — столбец и строку. Она вернет номер блока после выполнения нескольких вложенных условий. Знание номера блока будет иметь решающее значение для следующего шага.
Шаг 2.1. Определяем функцию хэш-карты
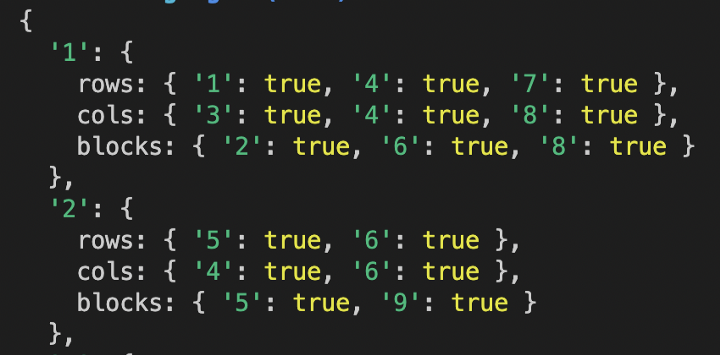
Выше показано, что я пытаюсь сделать. Эта хэш-карта сократит временную сложность решения, позволив проверить, имеется ли то или иное число в любой заданной строке, столбце или блоке. Просто связываем объект map с проверяемыми параметрами. Если нужно проверить, можно ли поместить число 2 в блок 5, я выполню следующее: map[2][blocks][5]. Это вернет true, потому что число уже там есть.
Такой ход действий избавляет от необходимости перебирать каждую из 81 ячейки игрового поля для каждого помещаемого в него числа. Проверка 9 чисел в 9 строках и в 9 столбцах может потребовать 729 операций. И пришлось бы повторять это до тех пор, пока головоломка не будет решена, что существенно увеличит временные затраты.
Создание хэш-карты позволяет пройтись по судоку только один раз в начале каждой рекурсии.
Ниже я прокомментировал шаги в функции, которую использовал для создания вышеупомянутой карты.
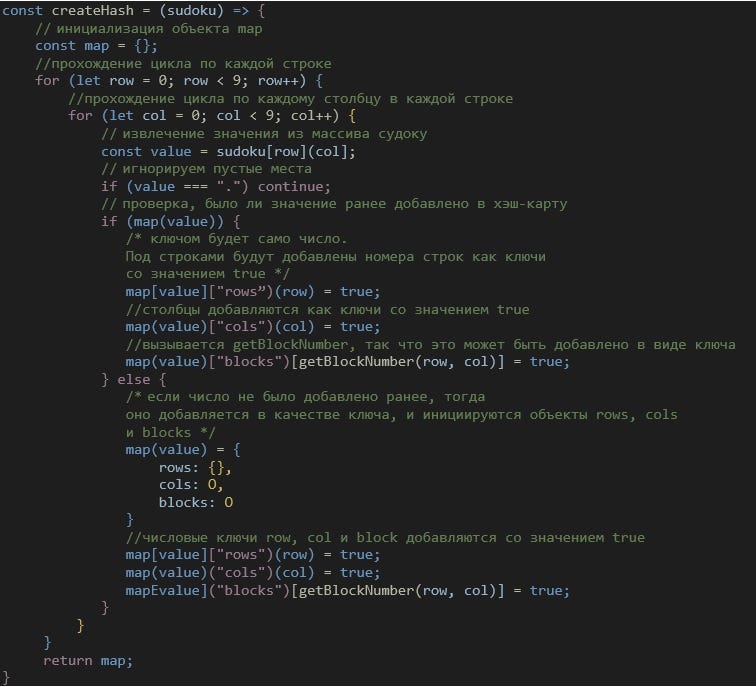
Шаг 3. Определяем возможность поместить число

Этот шаг — один из самых простых благодаря хэш-карте. Функция принимает строку, столбец, число и хэш-карту. Затем она проверяет, стоит ли число где-то еще в этой строке, столбце или в том же блоке. Это делается без необходимости цикличного прохождения. Если все три результата проверки оказываются ложными (то есть числа нет ни в строке, ни в столбце, ни в блоке), возвращается true.
Шаг 4. Выясняем, можно ли поместить число в любое другое место блока
Логика этого шага довольно проста. Сначала выполняется предыдущая функция, чтобы узнать, можно ли поместить число в текущую позицию. Допустим, у нас есть число, которое может быть определено в конкретное место. Затем проводится более тщательный поиск. Запускается следующая функция, чтобы узнать, может ли число находиться в другом месте. Если число может находиться именно здесь, а не где-либо еще, то его место определено.
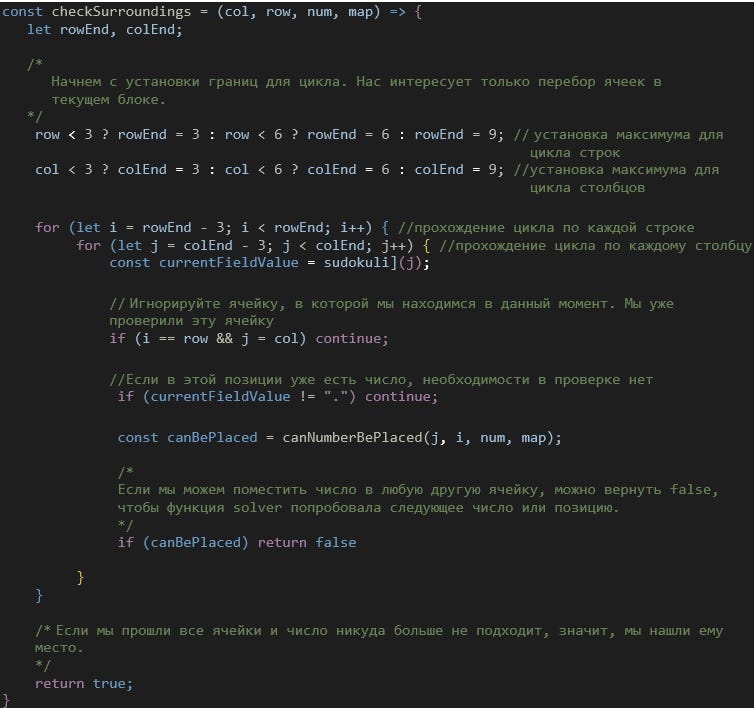
Шаг 5. Запускаем хэш-карту и начинаем решать
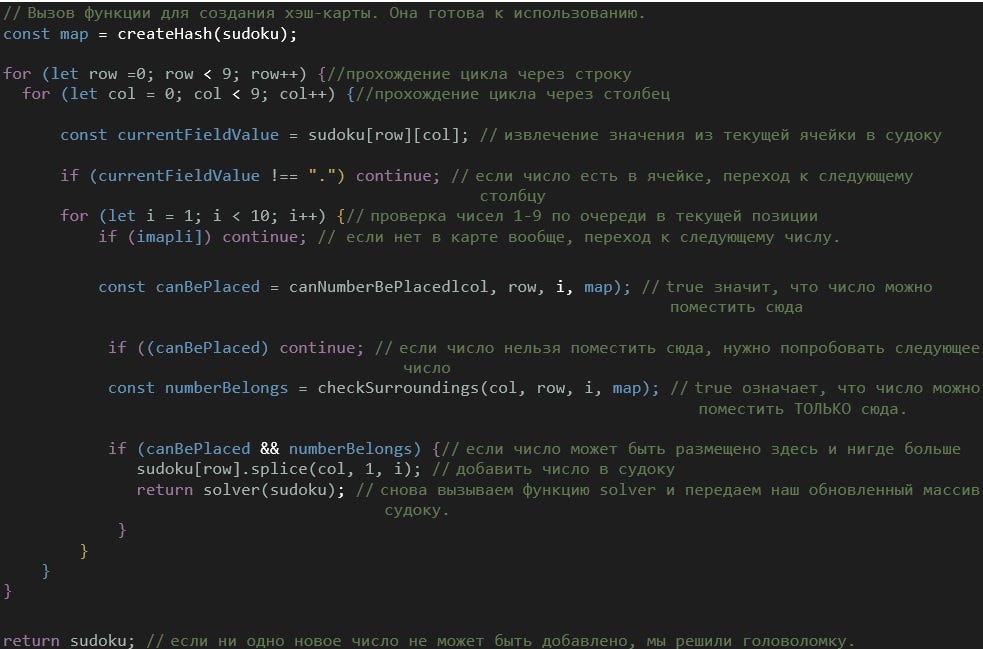
Пришло время использовать новые функции. Сначала вызывается функция для построения хэш-карты и начинается циклическое прохождение по массиву судоку. Она будет выполнять цикл только один раз и проверять каждое число от 1 до 9 в каждой позиции. Найдя число, которое можно добавить, она это сделает.
Последняя часть процесса является ключевой. Внутри return функция вызовет саму себя. Она передаст массив судоку (в котором теперь на одно число больше, чем раньше). Эта процедура будет продолжаться до тех пор, пока не наступит момент, когда больше нельзя будет добавить ни одного числа. В последней рекурсии судоку вернется в исходную функцию. А последним возвратом будет решенное судоку!
Используйте console.table, чтобы увидеть судоку в виде аккуратной таблицы.
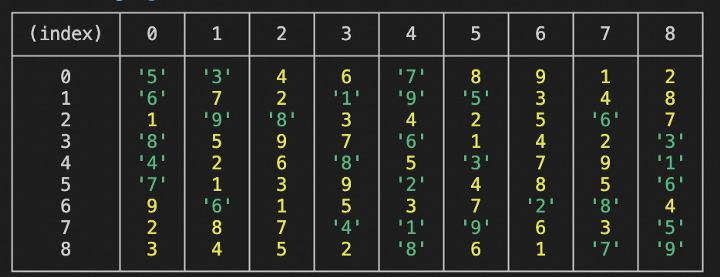
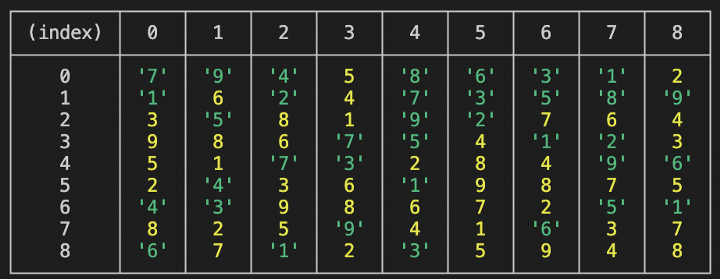
Вы можете решать головоломки более сложного уровня с помощью дополнительных проверок. Есть также возможность создать хэш-карту в первом вызове функции и просто изменить и передать хэш-карту при следующем вызове функции вместе с обновленным массивом судоку (как упоминалось ранее). Таким образом, не потребуется цикл для создания карты при каждой рекурсии.
Ссылка на репозиторий GitHub для тех, кто хочет попробовать улучшить эту функцию.
Читайте также:
- Чистый код JavaScript: 8 простых приемов
- Почему разработчики JavaScript используют инструменты на Rust
- Создание музыкального бота с помощью Discord.js
Читайте нас в Telegram, VK и Дзен
Перевод статьи Eddie Espinosa: Solving a Sudoku puzzle with JavaScript using hash maps and recursions






