Рекурсия является одним из наиболее мощных подходов в программировании. С ее помощью можно решать чрезвычайно сложные задачи, печатая при этом невероятно малый объем кода. Тем не менее понимание данного принципа нередко вызывает сложности, поскольку для этого требуется нестандартный взгляд на процесс выполнения команд.
Сложность примеров, описанных в данной статье, будет возрастать постепенно, начиная от самых простых и заканчивая достаточно трудными. При этом каждый из них будет сопровождаться подробной диаграммой:
- Рекурсивный способ мышления.
- Рекуррентные соотношения.
- Мемоизация.
- Стратегия “разделяй и властвуй”.
Рекурсия используется для решения задач, в которых функция вызывает сама себя в рамках собственного определения. В каждой реализации рекурсии должно присутствовать два элемента:
- Заключительный базовый кейс или кейсы, в которых рекурсивный поиск ответа более не производится.
- Набор правил (рекуррентных соотношений), который инициирует очередные циклы рекурсии, сводя таким образом общие кейсы к базовому.
В качестве примера давайте рассмотрим задачу по выводу развернутого варианта строки. В этом случае на выходе из вводного слова ‘hello’ должно получиться ‘olleh’. Итеративный метод решения этой задачи — применение цикла for и вывод каждого знака, начиная с последнего и заканчивая первым.

В рекурсивном же подходе мы сначала создаем функцию reverseString, получающую интересующую нас строку в качестве параметра. Если длина ввода не равна 0, то такой кейс является базовым или заключительным, и мы выводим последнюю букву, а затем инициируем еще один экземпляр reverseString для той же строки, исключив последнюю букву, поскольку ее мы уже вывели.
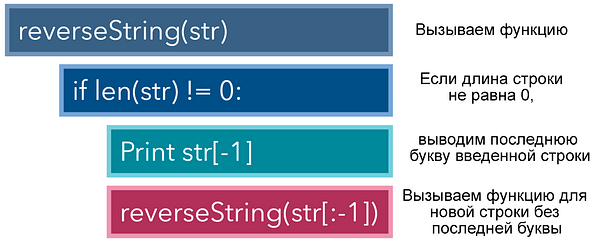
Обратите внимание: поскольку функция вызывается изнутри себя, она сама создает цикл for. Кроме того, наличие инструкции if перед вызовом другого экземпляра функции обязательно, в противном случае будет выброшена ошибка RecursionError или RuntimeError, поскольку скрипт не увидит конца бесконечного цикла. Данная ситуация аналогична бесконечному циклу While True.
Давайте посмотрим, как эта рекурсивная функция работает с ‘hello’:
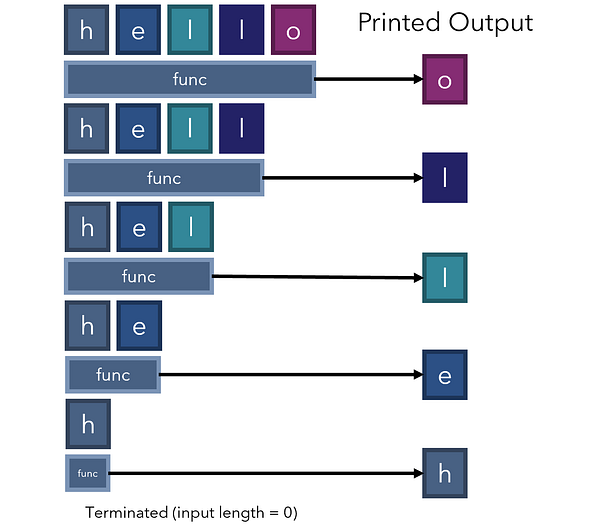
Рекуррентность в более сложных задачах может вызвать трудности при определении двух ее компонентов — рекуррентного соотношения, т.е. соотношения между результатом задачи и результатом ее подзадач и базовым кейсом, представляющим кейс, который можно вычислить напрямую без дополнительных рекурсивных вызовов. Иногда базовые кейсы называются “нижними кейсами”, потому что они являются кейсами, в которых задача уменьшена до наименьшего масштаба.
Рассмотрите в качестве примера треугольник Паскаля, в котором каждое число является суммой двух, находящихся над ним, и который имеет по сторонам единицы. Как можно использовать рекурсию для нахождения значения любого значения в точке (i, j)? Каково будет рекуррентное соотношение и базовый/заключительный кейс?
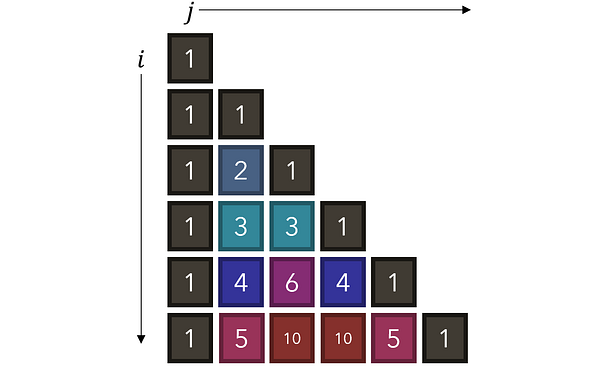
Рекуррентное соотношение можно выразить следующим уравнением:
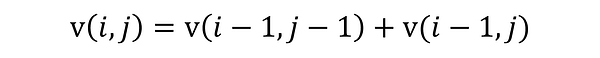
Это очевидно, когда смотришь на график треугольника. Еще более примечательно в этой формуле то, что если мы продолжим с ее помощью разбивать любую точку (i, j) на сумму двух других точек, то в итоге неизбежно получим базовый кейс — 1. Треугольник Паскаля начинается с единиц, и из их сумм строится весь сложный паттерн.
Как же нам это реализовать?
Для начала давайте найдем набор правил, чтобы определять, когда выполняется базовый кейс, при котором значение ячейки равняется 1. Обратите внимание, что 1-цы появляются при выполнении одного из двух условий: когда располагаются либо в первом столбце (j=0), либо по диагонали (i=j).
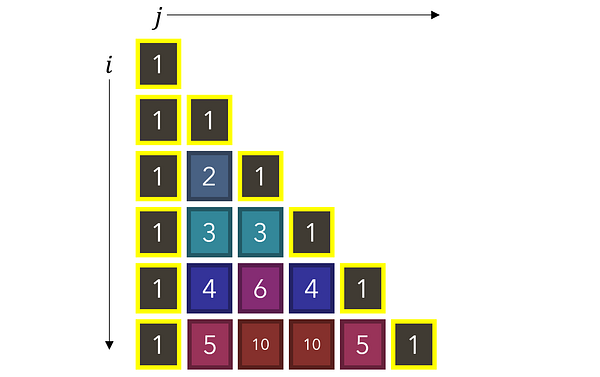
Теперь выполнить реализацию просто. Если условия для базового кейса выполнены, мы возвращаем базовое значение (1). В противном случае мы продолжаем уменьшать задачу до тех пор, пока не достигнем базового кейса, до которого, как мы определили, будет неизбежно разбит любой ввод.

Теперь рекурсия раскрылась для вас во всей красе. Здесь, с помощью всего пяти строк кода, мы, по сути, создаем саморазвивающееся дерево. При желании число строк кода можно даже уменьшить до трех. Вызывая функцию pascal дважды, мы инициируем две ветви поиска, каждая из которых также инициирует еще две, предполагая, что базовый кейс достигнут не был.
Такая эффективность рекурсии может показаться магической и даже может запутать. Давайте рассмотрим работу ее алгоритма на примере.
В соответствии с нашим рекуррентным соотношением (4, 2) разбивается на (3, 1) и (3, 2), которые являются двумя числами, стоящими над ней. Обратите внимание, что алгоритм на деле не знает, что значения этих ячеек представлены 3. Он просто учитывает их местоположение. Мы не знаем или даже не интересуемся никакими значениями, пока выполняются базовые условия. На основе базовых кейсов (1) мы можем вычислить другие не базовые точки, но для начала должны быть найдены все базовые.
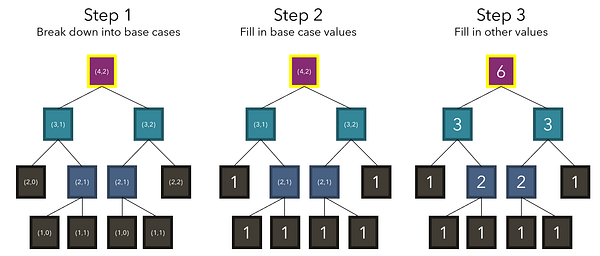
Согласно нашему рекуррентному соотношению, кейсы итеративно разбиваются до тех пор, пока не достигается базовый (j = 0 или i = j). Поскольку нам известны значения этих базовых кейсов (1), мы можем заполнить и другие значения, зависимые от базового кейса.
Это, конечно же, очень, а возможно и чересчур подробное представление принципа работы рекурсивного алгоритма. В действительности ни один из этих трех шагов не нужно программировать, так как они выполняются скриптом автоматически. Все, что вам нужно, — это вызвать функцию внутри ее самой и обеспечить ее завершение в некоторых точках при достижении базового случая.
При вызове return pascal(i-1, j) + pascal(i-1, j-1) мы рассматриваем возврат не как процесс, а как число. Поскольку pascal(i-1, j) инициирует собственные процессы ветвления, а в итоге возвращает другое число (например, 3), будет правильным воспринимать его именно как число, а не как процесс, что может вызвать ненужную сложность и затруднение в понимании.
С некоторой точки зрения этот рекурсивный алгоритм можно назвать неэффективным. В конце концов ‘6′ разбивается на ‘3′, которое, с позиции значения, имеет идентичные разбивки, но при этом зачем-то вычисляется второй раз. Это стандартный случай в рекурсии, когда базовые кейсы одного кейса, будучи вычисленными ранее, вычисляются повторно. Для устранения этой проблемы мы используем мемоизацию.
Возьмите в качестве примера последовательность Фибоначчи, в которой первые два числа представлены 0 и 1, а последующие числа являются суммой двух, им предшествующих. На основе уже сформированного знания мы понимаем, что базовыми кейсами здесь будут 0 и 1, а рекуррентное соотношение будет выглядеть как v(i) = v(i-2) + v(i-1). В таком случае мы можем построить простую рекурсивную функцию для нахождения значения последовательности Фибоначчи в любом индексе, начиная с 0.

Обратите внимание, что хоть это и грамотное применение рекурсии, оно весьма неэффективно. 8 разбивается на 3 и 5, а 5, в свою очередь, разбивается на 3 и 2. Мы вычисляем все с самого начала и строим завершенное дерево поиска со множеством повторений.
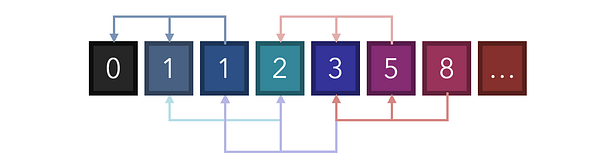
С помощью мемоизации мы можем решить эту проблему, создав кэш. Это можно реализовать, используя словарь и сохраняя значения, заданные ранее. Например, когда индекс 6 (значение 8) разбивается на индекс 4 и индекс 5 (значения 3 и 5), мы можем сохранить значение индекса 4 в кэше. При вычислении индекса 5 как индекса 3 плюс индекс 4 мы можем извлечь индекс 4 из кэша вместо того, чтобы повторно вычислять его, создавая еще одно обширное дерево, ведущее к базовым кейсам.
Чтобы включить в нашу функцию мемоизацию, мы добавим две функциональности: во-первых, если текущий индекс был сохранен в кэше, мы будем просто возвращать его сохраненное значение; во-вторых, прежде чем продолжать уменьшать значение, мы будем добавлять это значение к кэшу,чтобы ускорить дальнейшие операции. Обратите внимание, что кэш должен быть либо глобальной переменной, либо такой, которую можно извлечь и изменить независимо от области вызова команды.
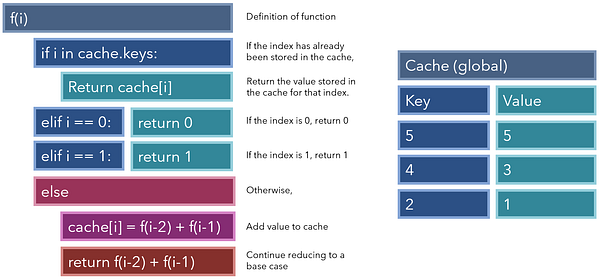
После добавления мемоизации наша рекурсивная функция стала намного быстрее и мощнее.
Рекурсия занимает центральное место среди многих наибыстрейших алгоритмов сортировки. Цель этих алгоритмов — получить список чисел и вернуть их в порядке от меньшего к большему. Поскольку очень много приложений опираются на быструю сортировку, весьма важно найти такой, который сможет сортировать списки максимально быстро. При этом некоторые из самых быстрых алгоритмов используют рекурсивный подход, называемый “разделяй и властвуй”.
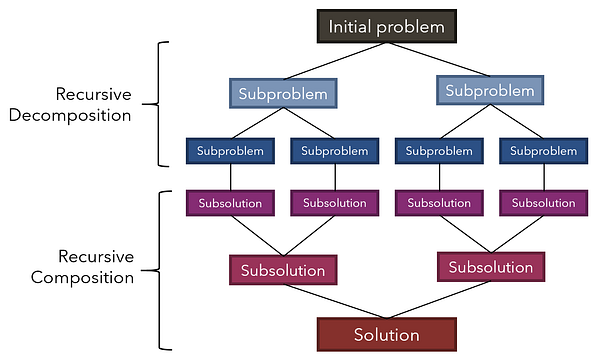
В стратегии “разделяй и властвуй” изначальная задача рекурсивно разбивается на несколько подзадач. После того, как каждая подзадача достигает размера единицы (аналог базового кейса), выявляются их подрешения, которые вновь рекурсивно совмещаются для формирования окончательного решения.
Рассмотрите, к примеру, QuickSort — один из наиболее быстрых алгоритмов сортировки, который при грамотной реализации может выполняться в 2–3 раза быстрее своих соперников и предшественников.
QuickSort начинает выполнение с выбора “опоры”. В простейших реализациях и для наших целей такую опору можно выбрать произвольно. Однако в более специализированных реализациях к ее выбору уже стоит подходить осторожно.

Все элементы со значениями меньше опоры переносятся левее нее, а все, чьи значения больше — правее. Выполнить это можно, пройдя по каждому элементу и переместив те, что меньше опоры, в один список, а те, что больше нее — в другой. Заметьте, что эта операция справляется с задачей только частично.
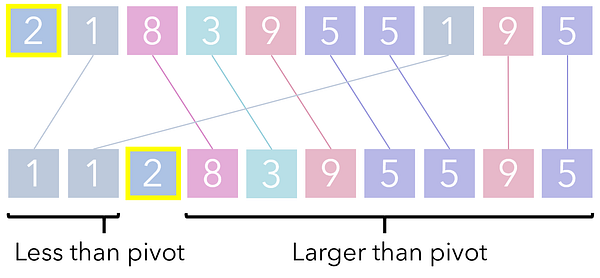
Процесс сортировки списка на основе его опорной точки называется разделением, так как опора разделяет этот список на два раздела, иначе говоря, на две стороны. Каждый их этих разделов вызывает очередную итерацию разделения сам на себя и так продолжается до тех пор, пока раздел не достигнет базового кейса (1 единицы, просто одного числа)
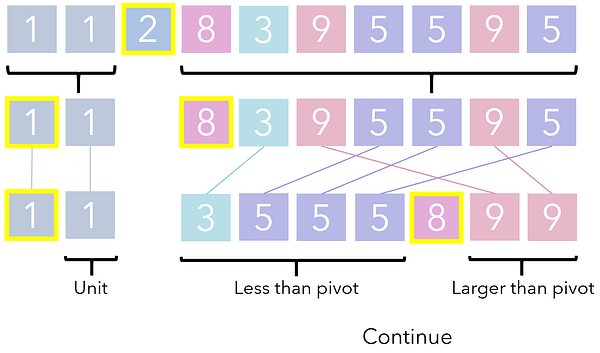
После достаточного числа рекурсивных вызовов исходный список будет разделен до точки, когда эти вызовы продолжить уже невозможно. В этой точке композиция подрешений выполняется простым составлением их в горизонтальном порядке. Результат такой композиции — отсортированный список.
Обратите внимание, что QuickSort следует многим из перечисленных основ рекурсии, рассмотренных нами ранее, только на более высоком уровне. Рекуррентное соотношение является разделением компонента, а базовый кейс — это разделение размера 1. Начиная с оригинального списка, те же процессы (выбор опоры и разделение) вызываются рекурсивно до тех пор, пока результат не будет состоять только из базовых кейсов.
Ключевые моменты
- Рекурсия — это подход программирования, в котором функция вызывает сама себя, допуская использование циклов и автоматическое построение дерева при минимальном количестве кода.
- При построении рекурсивной функции нужно четко понимать два ее основных элемента: рекуррентное соотношение и базовый кейс.
- Мемоизация — это метод, используемый для предотвращения повторения операций, работающий посредством сохранения информации в кэше с последующим ее извлечением при необходимости.
- Стратегия “разделяй и властвуй” — это одно из многих применений рекурсии, в котором задача рекурсивно разбивается на несколько подзадач (базовых кейсов), из которых можно с легкостью извлечь подрешения и агрегировать их в полноценное решение.
Читайте также:
- Почему в базе данных происходит взаимоблокировка?
- Слабо контролируемое обнаружение объектов - сквозной цикл обучения
- Выбор оптимального алгоритма поиска в Python
Читайте нас в Telegram, VK и Дзен
Перевод статьи Andre Ye: Advanced Concepts in Recursion Every Effective Programmer Should Know