Парадокс Монти Холла — это одна из тех математических задач, над решением которой уже долгое время бьются многие умы, и даже всемирно известных математиков она приводит в затруднение. Хотя идея, лежащая в основе этого парадокса, предельно ясна и понятна. Задача эта, строго говоря, и не парадокс вовсе, но называется так из-за неочевидности и парадоксальности предлагаемых решений и объяснений, которые становятся поводом для самых жарких дискуссий в Интернете. Их накал уступает, пожалуй, лишь спорам из-за оптической иллюзии так называемого «платья раздора» и аудиоиллюзии «Янни и Лорел». Предлагаемое здесь объяснение призвано раз и навсегда развеять все связанные с этим парадоксом вопросы и очень доходчиво разъяснить всем интересующимся его суть.

Парадокс
Парадокс впервые был сформулирован американским математиком Стивом Селвином ещё в 1975 году, но широкую известность он приобрёл благодаря популярному игровому шоу «Давайте заключим сделку». В честь ведущего этой телевикторины, которого звали Монти Холл, парадокс и получил своё название.
В чём же суть парадокса Монти Холла?
Представьте, что перед вами три двери, как показано на рисунке ниже. За двумя дверьми находятся козы, за одной — автомобиль. Надо угадать дверь с автомобилем, и он ваш.

Казалось бы, ничего сложного. Но, как говорилось в одном фильме: «Если бы задача так просто решалась, то армянское радио этим бы не занималось». В своей передаче, после того как участник выбирал дверь, Монти всегда открывал одну из дверей с козой и предлагал ему поменять свой выбор. А вы поменяли бы или нет?
Этот вопрос многих ставит в тупик. Люди обычно думают: «Ну какая разница: остались две двери, и машина может с одинаковой вероятностью 50% оказаться как за одной, так и за другой дверью?». … И оказываются неправы. Правильный ответ — всегда менять первоначальный выбор. Поступая так, вы удваиваете свои шансы на победу.
Удивлены? Такой ответ для многих становится откровением: мало кто ожидает этого. Давайте подробно разберёмся, как так получается.
Итак, вы выбрали одну из трёх дверей. Вероятность того, что машина окажется именно за ней, составляет 1/3. А вероятность того, что она окажется за одной из двух оставшихся (то есть не выбранных вами) дверей, будет 2/3. Это должно быть понятно.
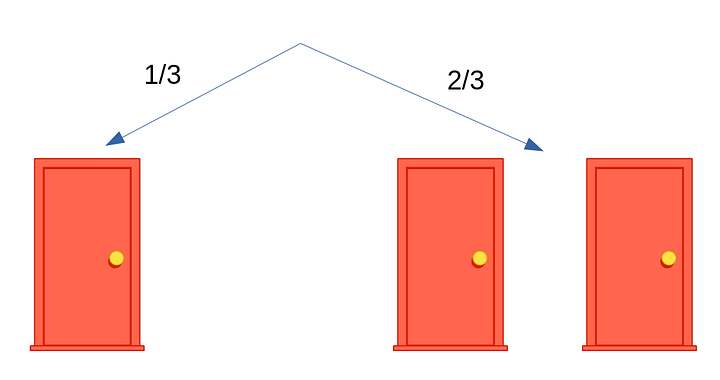
На рисунке у нас наглядно показаны эти вероятности: 1/3 слева и 2/3 справа.
Теперь Монти открывает одну из невыбранных дверей — тех, что справа. И открывает он всегда ту, за которой коза.
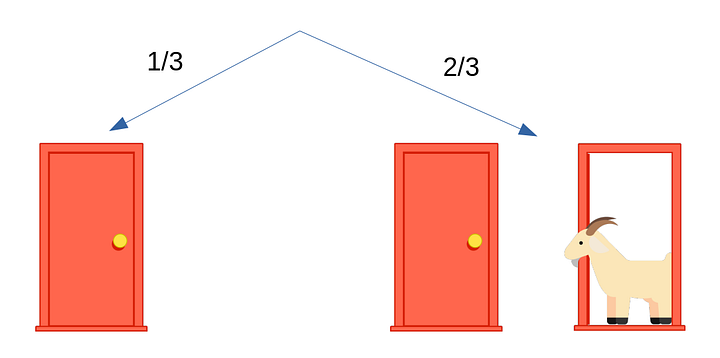
Вероятности остаются неизменными: 1/3 слева (ваш первоначальный выбор) и 2/3 справа. Изменилось лишь то, что справа одна дверь теперь открыта, но вероятность для оставшейся неоткрытой двери здесь та же, что была прежде для обеих.
Если не совсем понятно, попробуем объяснить на примере с десятью дверьми.

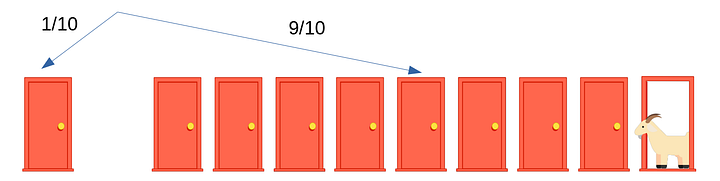
Выбранная вами дверь будет слева, остальные девять — справа (как на рисунке ниже). Вероятность того, что вы угадали дверь с машиной, будет 1/10. Вероятность того, что вы не угадали и машина окажется за одной из оставшихся девяти дверей, будет 9/10.
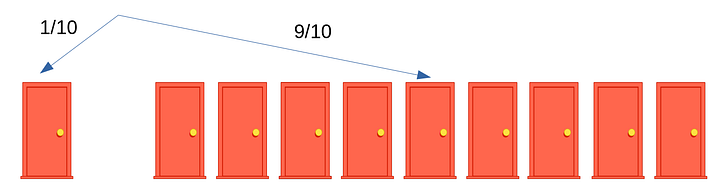
Дальше Монти открывает восемь из этих невыбранных девяти дверей, причем за всеми восемью — козы. Как поступить теперь: поменять свой выбор или нет? Конечно, поменять! Ведь теперь восемь из девяти дверей справа открыты, а вероятность того, что машина окажется за оставшейся девятой дверью (как мы уже посчитали ранее), равна 9/10.
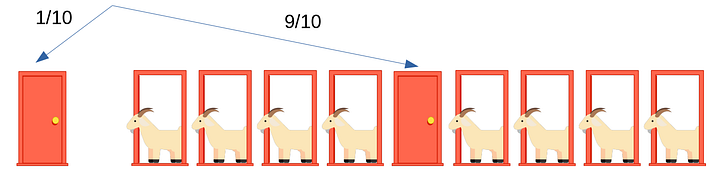
Ответ на вопрос станет ещё очевиднее, если представить, что Монти даёт вам возможность открыть не одну оставшуюся справа неоткрытой дверь, а сразу все девять!
Вот и всё. Это так просто! Однако важно не забывать, что всегда есть вероятность проигрыша. Верное решение определяется стратегией. Правильная стратегия — делать так, чтобы шансы на победу были максимальными или хотя бы такими, которые позволяют больше выигрывать, чем проигрывать.
Усложняем задачу
Предположим, Монти хочет усложнить для вас задачу и открывает лишь одну дверь с правой стороны. Как вы поступите теперь: выберите одну из восьми закрытых дверей справа или не станете менять свой выбор?
Здесь придётся кое-что посчитать. Вероятность того, что машина окажется за одной из девяти дверей справа, равна 9/10. Разделим её на количество оставшихся неоткрытыми дверей (8):
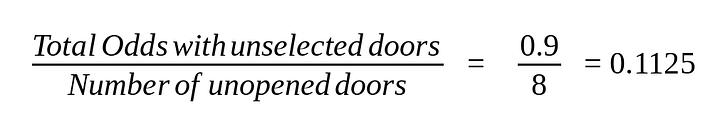
Это будет вероятность того, что машина окажется за одной из восьми остающихся закрытыми дверей справа. И она чуть больше вероятности 0,1 (1/10), что первоначально выбранная вами дверь слева окажется с машиной. Поэтому вам всё же предпочтительнее поменять свой выбор, хотя шансы выиграть машину и в этом случае будут очень низкими. По этой же формуле можно посчитать вероятность для любого количества неоткрытых дверей.
Вот и весь парадокс Монти Холла вкратце. Не знаю, можно ли придумать более простое его объяснение? Я лишь выношу на ваш суд свой взгляд, отличный от тех, что изложены в большинстве других объяснений, в которых вы можете тоже почерпнуть много полезного. Надеюсь, что после прочтения статьи вы приблизились к пониманию парадокса Монти Холла.
Читайте также:
- Руководство по машинному обучению для новичков
- JavaScript Essentials: числа и математика
- Завораживающая последовательность Фибоначчи
Перевод статьи Anup Sebastian: The easiest explanation to the Monty Hall problem






