Цель этой статьи — объяснить не то, как работает механизм самовнимания в трансформерах, а скорее то, почему он был разработан именно таким образом.
Начнем с обсуждения того, какими способностями должна обладать модель интерпретации языка. Затем последует интерактивное создание механизма самовнимания. В процессе вы узнаете, что использование запросов, ключей и значений позволяет естественным образом моделировать отношения между словами, и что QKV-внимание — один из простейших способов решения этой задачи.
Статья рассчитана прежде всего на тех, кто уже сталкивался с трансформерами и самовниманием. Тем не менее она будет понятна любому, кто знаком с основами линейной алгебры.
Все использованные изображения созданы автором.
Трансформеры обычно рассматриваются в контексте задач моделирования “от последовательности к последовательности” (sequence-to-sequence), таких как языковой перевод или, что более важно, завершение предложений. Однако нам проще начать с задачи моделирования последовательности, в частности интерпретации языка.
Итак, вот предложение, которое нужно интерпретировать:

Немного поразмыслим над тем, как мы понимаем это предложение.
- Evan’s dog Riley… (Собака Эвана Райли…). Из этих слов мы понимаем, что Райли — это кличка собаки, а Эван — владелец Райли.
- …is so hyper… (…гиперактивна…). Тут все достаточно просто: “гиперактивна” относится к собаке Райли и определяет наше впечатление о Райли.
- …she never stops moving (…она все время находится в движении). Это уже интересней: “she” относится к Райли, так как собака является субъектом первой фразы. “She” указывает на то, что Райли женского пола, что ранее было неясно из-за того, что кличка подходит собакам обоих полов. “Never stops moving” — более сложный набор слов, который раскрывает значение слова “hyper”.
Ключевой вывод из этого упражнения такой: для интерпретации смысла предложения мы постоянно учитываем, как одни слова соотносятся с другими словами, дополняя их значение.
В сообществе машинного обучения процесс дополнения значения слова a за счет присутствия слова b называется “a соотносится с b” (“a attends to b”), то есть слово a “обращает внимание” на слово b.
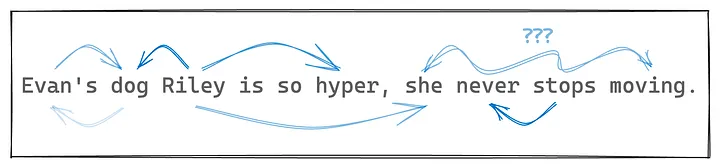
Итак, чтобы модель машинного обучения могла интерпретировать язык, она должна уметь соотносить одно слово с другим и соответствующим образом дополнять его значение.
Именно эту способность мы будем имитировать, создавая в 3 этапа механизм, называемый (само)вниманием.
В процессе работы вам будут предложены вопросы, выделенные курсивом. Рекомендую задуматься над каждым из них и попытаться ответить, прежде чем продолжить чтение.
Этап 1
На данном этапе сосредоточимся на отношениях между словами “dog” (“собака”) и “Riley” (“Райли”). Поскольку слово “dog” сильно влияет на значение слова “Riley”, нам нужно, чтобы “Riley” соотносилось с “dog”. Наша цель в данном случае — дополнить значение слова “Riley” соответствующим образом.
Чтобы конкретизировать этот пример, начнем с векторных представлений каждого слова (каждое длиной n), основанных на контекстно-независимой интерпретации слова. Будем считать, что это векторное пространство достаточно хорошо организовано, то есть слова, более схожие по смыслу, ассоциируются с векторами, ближе расположенными в пространстве.
Итак, у нас есть два вектора, v_dog и v_Riley, которые отражают значение двух слов.
Как дополнить значение v_Riley, используя v_dog, чтобы получить новое значение для слова “Riley”, включающее в себя значение слова “dog”?
Нам не нужно полностью заменять значение v_Riley на v_dog, поэтому допустим, что дополненным значением для v_Riley будет линейная комбинация v_Riley и v_dog:
v_Riley = get_value('Riley')
v_dog = get_value('dog')
ratio = .75
v_Riley = (ratio * v_Riley) + ((1-ratio) * v_dog)
Вроде бы все нормально: мы вложили часть значения слова “dog” в слово “Riley”.
Теперь попробуем применить эту форму внимания ко всему предложению, дополняя векторные представления каждого слова векторными представлениями каждого другого слова.
Что здесь не так?
Основная проблема заключается в том, что мы не знаем, какие слова должны принимать значения других слов. Кроме того, нам необходимо получить некую меру того, насколько значение каждого слова должно влиять на значение каждого другого слова.
Этап 2
Итак, нам нужно узнать, насколько сильно должны быть связаны два слова.
Настало время для попытки номер 2.
Перестроим базу данных векторов так, чтобы каждое слово имело два ассоциированных вектора. Один из них — тот же, что и раньше у нас был, вектор значений, обозначаемый v. Кроме того, у нас теперь появятся единичные векторы, обозначаемые k, хранящие некое представление об отношениях между словами. В частности, если два k-вектора расположены близко друг к другу, это означает, что значения, ассоциируемые с этими словами, скорее всего, влияют на смысл друг друга.
Как изменить предыдущую схему с помощью новых векторов k и v, чтобы v_dog дополнил v_Riley с учетом того, насколько сильно связаны два слова?
Продолжим с тем же линейным комбинированием, что и раньше, но только в том случае, если оба k-вектора близки в пространстве встраивания. При этом мы можем использовать скалярное произведение двух k-векторов (которое находится в диапазоне 0–1, поскольку это единичные векторы), чтобы выяснить, насколько сильно должен v_dog дополнить v_Riley.
v_Riley, v_dog = get_value('Riley'), get_value('dog')
k_Riley, k_dog = get_key('Riley'), get_key('dog')
relevance = k_Riley · k_dog # скалярное произведение
v_Riley = (relevance) * v_Riley + (1 - relevance) * v_dog
Немного странно: если показатель релевантности равен 1, то v_Riley должен полностью замениться v_dog. Но давайте пока проигнорируем это.
Подумаем вот о чем: что произойдет, если применить такой подход ко всей последовательности? Значение слова “Riley” будет релевантно значению каждого другого слова благодаря скалярному произведению k-векторов. Поэтому, возможно, получится дополнить значение каждого слова пропорционально значению скалярного произведения. Для простоты также включим его скалярное произведение с самим собой, чтобы сохранить его собственное значение.
sentence = "Evan's dog Riley is so hyper, she never stops moving"
words = sentence.split()
# получение списка значений
values = get_values(words)
# вот что значит k
keys = get_keys(words)
# получение ключа релевантности для riley
riley_index = words.index('Riley')
riley_key = keys[riley_index]
# генерация релевантности Riley по отношению к каждому другому слову
relevances = [riley_key · key for key in keys] # все еще допуская, что в python есть ·
# нормализуем релевантность, чтобы ее сумма равнялась 1
relevances /= sum(relevances)
# принимает линейную комбинацию значений, взвешенных по релевантности
v_Riley = relevances · values
Пока этого достаточно.
Но нужно снова признать некорректность данного подхода. Дело не в том, что какая-либо из идей была реализована неправильно, скорее есть нечто фундаментально отличающееся между этим подходом и тем, как мы на самом деле рассуждаем об отношениях между словами.
Если в этой статье и есть момент, когда вам действительно стоит задуматься, то именно в этом месте. Даже тем из вас, кто считает, что полностью разбирается в теме. Что не так с нашим подходом?
Отношения между словами по своей природе ассиметричны! То, как “Riley” относится к “dog”, отличается от того, как “dog” относится к “Riley”. То, что “Riley” относится к собаке, а не к человеку, имеет гораздо большее значение, чем то, что это кличка собаки.
Между тем, скалярное произведение является симметричной операцией, а это значит, что в текущей установке действует правило: если a относится к b, то b относится к a в той же мере! Это несколько неточно, поскольку мы нормализуем показатели релевантности, но смысл в том, что слова должны иметь возможность асимметричной привязки, даже если другие лексемы остаются неизменными.
Этап 3
Мы почти у цели! Возникает вопрос:
Как наиболее естественным образом расширить текущую установку, чтобы обеспечить возможность асимметричных отношений?
Можно ли это сделать, добавив новый тип вектора? У нас по-прежнему остаются вектор значений v и вектор отношений k. Теперь добавим вектор запроса q для каждой лексемы.
Как изменить текущую установку, используя q для достижения асимметричных отношений?
Тех, кто понимает, как работает самовнимание, это может повеселить.
Вместо того чтобы вычислять релевантность k_dog · k_Riley, если “dog” соотносится с “Riley”, можно запросить q_Riley по ключу k_dog, взяв их скалярное произведение. При вычислении в обратном направлении получим q_dog · k_Riley — асимметричная релевантность!
Вот все это вместе, с вычислением дополнения для каждого значения сразу.
sentence = "Evan's dog Riley is so hyper, she never stops moving"
words = sentence.split()
seq_len = len(words)
# получение массивов запросов, ключей и значений, каждый из которых имеет форму (seq_len, n)
Q = array(get_queries(words))
K = array(get_keys(words))
V = array(get_values(words))
relevances = Q @ K.T
normalized_relevances = relevances / relevances.sum(axis=1)
new_V = normalized_relevances @ V
Это и есть самовнимание!
Некоторые детали я опустил, но важные идеи все здесь.
Напомню, мы начали с векторов значений (v) для представления значения каждого слова, но быстро обнаружили, что нам нужны векторы ключей (k) для учета того, как слова соотносятся друг с другом. Чтобы правильно смоделировать асимметричную природу отношений между словами, мы ввели векторы запросов (q).
Выходит, если все, что нам нужно, — это скалярные произведения и тому подобное, то 3 — минимальное количество векторов на слово, необходимое для правильного моделирования отношений между словами.
Цель этой статьи — через механизм самовнимания показать, что он является менее громоздким, чем традиционный подход “сперва алгоритм” (“algorithm-first”). Надеюсь, с этой точки зрения, более ориентированной на естественный язык, элегантность и простота конструкции “запрос-ключ-значение” (query-key-value) являются очевидными.
Детали, которые были упущены выше:
- Вместо того, чтобы хранить 3 вектора для каждой лексемы, достаточно хранить один вектор встраивания, из которого можно извлечь q-k-v векторы. Процесс извлечения — просто линейная проекция.
- Технически во всей этой схеме каждое слово не имеет представления о том, где находятся другие слова в предложении. Самовнимание — это операция с множеством. Поэтому нужно применить знания о позиционной системе, что обычно делается путем добавления позиционного вектора к вектору встраивания. Это не совсем тривиально, поскольку трансформеры должны допускать последовательности произвольной длины. То, как это работает на практике, выходит за рамки данной статьи.
- Один слой самовнимания позволяет представлять только двухсловные отношения (между двумя словами). Но, компонуя слои самовнимания, можно моделировать отношения между словами на более высоком уровне. Поскольку выход слоя самовнимания имеет ту же длину последовательности, что и исходная последовательность, их можно скомпоновать. Фактически блоки трансформеров — это просто слои самовнимания, за которыми следуют позиционные блоки прямой связи. Сложите несколько сотен таких блоков, заплатите несколько миллионов долларов, и получите LLM.
Читайте также:
- Python-библиотеки интерпретации моделей ML
- Как язык SudoLang помогает общаться с языковыми моделями. Руководство для новичков
- BabyAGI — автономный ИИ-агент для оптимизации задач
Читайте нас в Telegram, VK и Дзен
Перевод статьи Ryan Xu: Motivating Self-Attention






