Прежде чем вводить параметр λ и подставлять его в формулу, давайте задумаемся: почему Пуассону вообще пришлось изобретать такое распределение?
1. Почему Пуассон изобрел свое распределение?
Чтобы предсказывать количествобудущихсобытий!
Или более формально: чтобы предсказывать вероятность данного числа событий, происходящих в определенный интервал времени.
В продажах, например, “событие” это покупка (сам момент покупки, не просто выбор). Событием может быть количество посетителей в день на веб-сайте, кликов на рекламном объявлении в следующем месяце, число звонков в рабочее время или число людей, которые умрут от смертельных заболеваний в следующем году, и так далее.
Вот пример, как я использую распределение Пуассона в реальной жизни.
Каждую неделю в среднем 17 человек оставляют лайк под моим постом в блоге.
Я хочу предсказать количество лайков на следующей неделе, потому что мои еженедельные выплаты зависят от этого количества.
Какова вероятность того, что точно 20 человек (или 10, 30, 50 и так далее) поставят лайк под моим постом на следующей неделе? 2. Как решить эту задачу?
Давайте на время сделаем вид, что мы ничего не знаем о распределении Пуассона. Как тогда решить задачу?
Первый путь: начать с количества прочтений. Для каждого читателя блога есть вероятность, что статья ему действительно понравится и он поставит лайк.
Это классическая работа для биномиального распределения, так как мы рассчитываем количество успешных событий (лайков).
Биномиальная случайная величина — это количество успешных x в n повторяющихся попыток. Предполагается, что вероятность успеха p является постоянной в каждой попытке.
Итак, у нас есть только один параметр — 17 человек в неделю, что является “средним значением” (средним значением успешных событий в неделею, или математическим ожиданием x). Нам ничего не известно ни о вероятности получения лайков p, ни о количестве посетителей блога n.
Значит, нам нужно больше информации для решения задачи. Что конкретно нужно, чтобы оформить эту вероятность как биномиальную проблему? Две вещи: вероятность успеха (лайков) p и количество попыток (посетителей) n.
Получим их из прошлых данных.
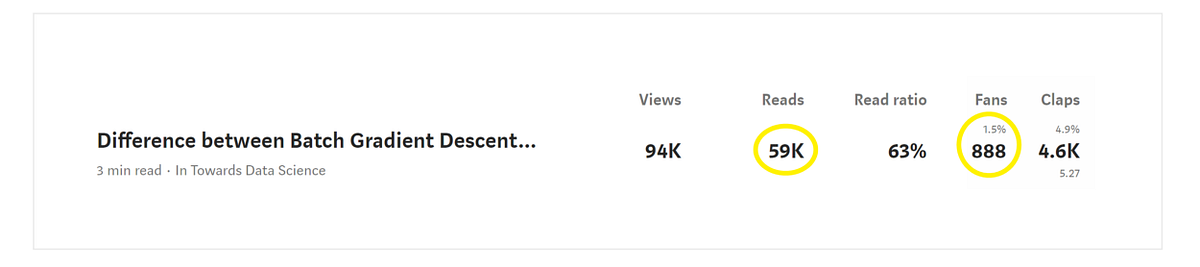
Это статистика за 1 год. Общее количество читателей блога — 59 тысяч, 888 из них поставили лайк.
Следовательно, количество читателей в неделю (n): 59 000/52 = 1134. Количество поставивших лайк в неделю (x): 888/52 =17.
количество читателей в неделю (n) = 59000/52 = 1134
количество оставивших лайк в неделю (x) = 888/52 = 17
вероятность успеха (p) : 888/59000 = 0.015 = 1.5%Используя биномиальную функцию вероятности, посчитаем вероятность того, что я получу точно 20 успешных событий (20 лайков) на следующей неделе.
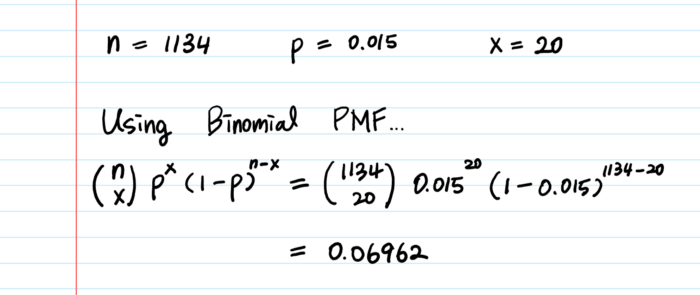
<Биномиальная вероятность для различных x>
╔══════╦═══════════════════╗
║ x ║ Binomial P(X=x) ║
╠══════╬═══════════════════╣
║ 10 ║ 0.02250 ║
║ 17 ║ 0.09701 ║ ? P выше у среднего показателя!
║ 20 ║ 0.06962 ║ ? Неплохо. 20 тоже вполне вероятно!
║ 30 ║ 0.00121 ║
║ 40 ║ < 0.000001 ║ ? Не думаю, что получу 40 лайков...
╚══════╩═══════════════════╝Только что мы решили задачу с помощью биномиального распределения.
Тогда зачем нам распределение Пуассона? Что оно может делать такого, что не может биномиальное распределение?
3. Недостатки биномиального распределения
a) Биномиальная случайная величина бинарна — 0 или 1.
В примере выше у нас было 17 лайков в неделю. Это 17/7 = 2.4 человека в день и 17/(7*24) = 0.1 в час.
Если моделировать вероятность успеха в часах (0.1 человек в час), используя биномиальную случайную величину, получим, что в большем количестве часов лайков будет 0, а в некоторые часы ровно 1 лайк. Также возможно, что в час будет больше 1 лайка (2, 3, 5 и т.д.).
Проблема с биномиальным распределением в том, что оно не может содержать более одного события в единицу времени (1 час в примере).
Так может разделить 1 час на 60 минут и принять за единицу времени минуту? Тогда в 1 час поместится несколько событий. (Помним, что 1 минута содержит только ноль или одно событие).
Теперь проблема решена?
Вроде бы. Но что если в течение одной минуты мы получим несколько лайков? (например, кто-то поделился постом в Твиттере, и трафик вырос в эту минуту). Что тогда? Можно разделить минуту на секунды. Тогда единицей времени становится секунда, и в минуту помещается несколько событий. Но проблема бинарного контейнера будет существовать для все меньших единиц времени.
Дело в том, что биномиальная случайная величина может содержать несколько событий, если делить единицу времени на все меньшие единицы. В результате изначальная единица времени будет содержать более одного события.
Математически это означает n → ∞. Если предположим, что среднее значение фиксировано, тогда p → 0. В противном случае n*p — количество событий — чрезмерно возрастет.
Единица времени с использованием этого лимита может быть бесконечно мала. Больше не нужно беспокоиться о более чем одном событии в единицу времени. Так получается распределение Пуассона.
b) В биномиальном распределении количество попыток (n) должно быть известно заранее.
Нельзя посчитать вероятность успеха при помощи биномиального распределения, зная только среднее значение (17 человек в неделю). Нужно больше информации (n и p), чтобы использовать формулу.
Распределение Пуассона же не обязывает вас знать ни n ни p. Предположим, что n бесконечно велико, а p бесконечно мала. Единственный параметр распределения — значение λ (ожидаемое значение x). В реальной жизни чаще известно только значение (например, с 2 до 4 часов дня я принял 3 телефонных звонка), а не значения n и p.
4. Формула Пуассона
Давайте получим формулу Пуассона математически из формулы функции биномиального распределения.

Теперь вы знаете, откуда берутся компоненты λ^k , k! и e^-λ!
Теперь нужно только показать, что умножение первых двух множителей n!/((n-k)!*n^k) дает1, когда n стремится к бесконечности.
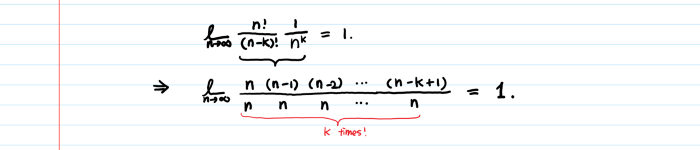
Это 1.
Мы получили формулу Пуассона!
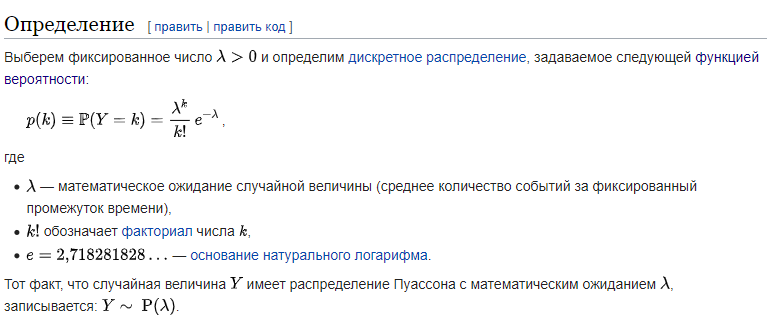
Теперь понятнее:
Введите ваши данные в формулу и проверьте даст ли P(x) необходимый результат!
Ниже мой:
< Сравнение биномиального распределения и распределения Пуассона > ╔══════╦═══════════════════╦═══════════════════════╗
║ k ║ Binomial P(X=k) ║ Poisson P(X=k;λ=17) ║
╠══════╬═══════════════════╬═══════════════════════╣
║ 10 ║ 0.02250 ║ 0.02300 ║
║ 17 ║ 0.09701 ║ 0.09628 ║
║ 20 ║ 0.06962 ║ 0.07595 ║
║ 30 ║ 0.00121 ║ 0.00340 ║
║ 40 ║ < 0.000001 ║ < 0.000001 ║
╚══════╩═══════════════════╩═══════════════════════╝
* Оба можно легко посчитать здесь:
Биномиальное: https://stattrek.com/online-calculator/binomial.aspx
Пуассона: https://stattrek.com/online-calculator/poisson.aspxНесколько замечаний:
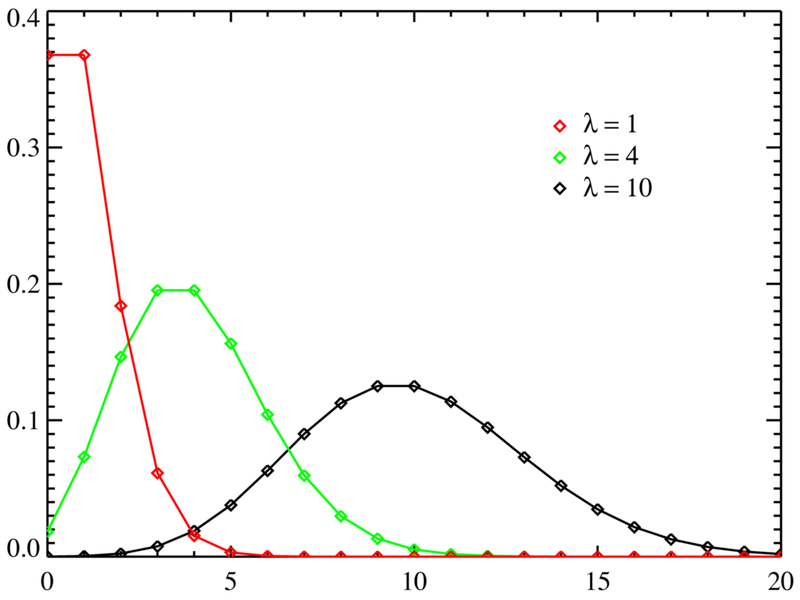
- Несмотря на то, что распределение Пуассона моделирует редкие события, значение λ может быть любым, оно не обязательно всегда должно быть маленьким.
- Распределение Пуассона асимметрично — оно всегда смещено вправо, потому что слева его ограничивает нулевой барьер (не существует такой вещи как “минус один” лайк), а справа ограничений нет.
- Чем больше становится значение λ, тем ближе график к графику нормального распределения.
4. Ограничения распределения Пуассона:
a. Среднее значение событий в единицу времени постоянно.
Что это значит? Количество людей, посещающих блог в час может не следовать распределению Пуассона, потому что значение посещений в час не является постоянным (‘значение n выше днем, ниже вечером). Использование значения за месяц для потребительских или биологических данных тоже будет лишь приблизительным, потому что сезонный эффект в этой области не предсказуем.
b. События независимы.
Появление посетителей не всегда независимо. Например, посетители могут прийти группой, потому что кто-то популярный упомянул вас в своем блоге, или ваш блог оказался на первой странице сайта. Количество землетрясений в год в стране также может не соответствовать распределению Пуассона, если одно сильное землетрясение увеличивает вероятность последующих толчков.
5. Соотношение между распределением Пуассона и экспоненциальным распределением.
Если количество событий в единицу времени соответствует распределению Пуассона, тогда период времени между событиями соответствует экспоненциальному распределению. Распределение Пуассона дискретно, а экспоненциальное непрерывно, но они тесно связаны.
Читайте также:
- Машинное обучение. С чего начать? Часть 1
- Как приобрести навыки, необходимые для выживания в мире современных технологий
Перевод статьи Aerin Kim: What is Poisson Distribution?