Цепь Маркова используют многие современные компании и организации. Она помогает прогнозировать погоду и разрабатывать маркетинговые стратегии, находит применение в различных приложениях для решения реальных задач конечных автоматов, таких как DFA.
В Python эта концепция представлена в системе вероятностного автомата. Изменения состояния системы называются переходами. Вероятности, связанные с различными изменениями состояния, называются вероятностями перехода. Вероятностный автомат превращает вероятность каждого перехода в функцию перехода и формирует переходную матрицу.
Как создать цепь Маркова
Представим себе такую ситуацию:
“Когда Си Джей грустит (что для нее не очень характерно), она либо отправляется на пробежку, либо поглощает мороженое, либо укладывается спать”.
Для создания цепи Маркова нам потребуется сначала создать переходную матрицу, в которой будут перечислены вероятности каждого перехода состояния. Другими словами, мы должны представить текущее состояние сегодняшним действием Си Джей, в то время как следующее состояние — ее завтрашним действием.
Вероятность перехода состояния будем рассматривать как вероятность того, что Си Джей выполнит одно из трех конкретных действий сегодня, а следующее действие, тоже одно, — завтра. Например, Си Джей отправится на пробежку сегодня, а завтра будет спать. Связав таким образом все вероятности перехода состояния, мы получим переходную матрицу, которая поможет создать цепь Маркова, описывающую конкретную ситуацию.
Наша матрица перехода — это матрица N x N, предполагающая, что N — это количество вероятных состояний. Итак, сначала мы должны определить количество состояний в нашей задаче. Поскольку нам дано три действия, которые Си Джей совершает, когда ей грустно, у нас есть 3 состояния. При этом важно учитывать, что Си Джей не может выполнять все 3 действия одновременно. Другими словами, она не может в одно и то же время спать и есть мороженое, так как ключевые слова в постановке задачи — либо одно действие, либо другое.
Главная идея цепи Маркова заключается в том, что существует только одно текущее состояние и, следовательно, один переход в одно следующее состояние. Это важное замечание поможет нам отслеживать наши вероятности.
Как уже говорилось выше, мы выделили 3 действия, которые совершает Си Джей, когда ей грустно, чтобы определить значение N, или количество состояний. Теперь мы должны создать переходную матрицу связанных вероятностей 3 х 3.
Пошаговый алгоритм процесса создания переходной матрицы
Предположим, что Си Джей грустит. В этом случае, как указано в задаче, нужно рассмотреть 3 вероятных состояния Си Джей:
- Отправляется на пробежку.
- Ест мороженое.
- Спит.
Если текущее состояние “спит”, то можно вычислить вероятность следующего состояния:
- “спит” — 20%;
- “отправляется на пробежку” — 60%;
- “ест мороженое” — 20%.
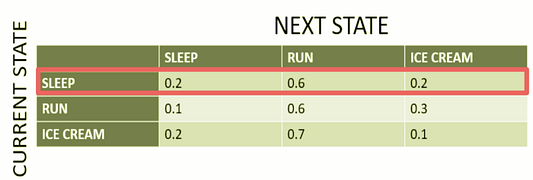
Мы выделили красным цветом строку, на которой сосредоточились, так как текущее состояние (как указано в заголовке строки слева) заключается в том, что Си Джей спит в течение сегодняшнего дня.
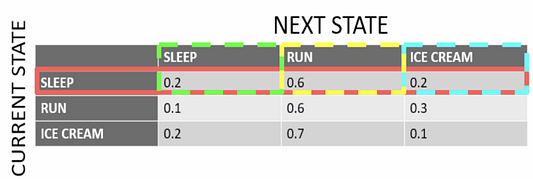
Столбцы представляют следующее состояние, учитывая, что текущее состояние заключается в том, что Си Джей спит. Вы можете видеть вероятность каждого перехода, например, когда Си Джей спит сегодня, вероятность того, что на следующий день она будет спать, равна 0,2; отправится на пробежку — 0,6; съест мороженое — 0,2. Три разных столбца выделены разными цветами, чтобы изолировать 3 разностные вероятности перехода состояний.
Если текущее состояние “собирается на пробежку”, то вероятность следующего состояния составит:
- “спит” — 10%;
- “собирается на пробежку” — 60%;
- “ест мороженое” — 30%.
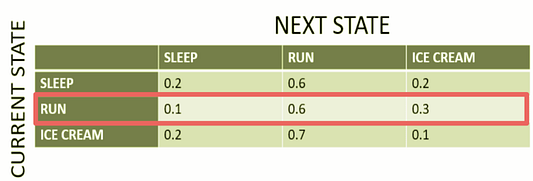
Мы выделили красным цветом строку, на которой сосредоточились, поскольку текущее состояние (как указано в заголовке строки слева) заключается в том, что Си Джей собирается на пробежку в течение сегодняшнего дня.
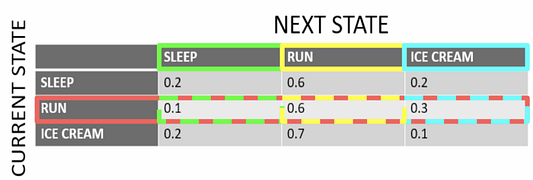
Столбцы представляют следующее состояние, учитывая, что текущее состояние заключается в том, что Си Джей собирается на пробежку. Вы можете видеть вероятности каждого перехода, например, когда Си Джей собирается на пробежку в текущий день, вероятность того, что на следующий день она будет спать, равна 0,1; пойдет на пробежку — 0,6; съест мороженое — 0,3. Три разных столбца выделены разными цветами, чтобы изолировать 3 разностные вероятности перехода состояний.
Если текущее состояние “ест мороженое”, то вероятность следующего состояния составит:
- “спит” — 20%;
- “собирается на пробежку” — 70%;
- “ест мороженое” — 10%.
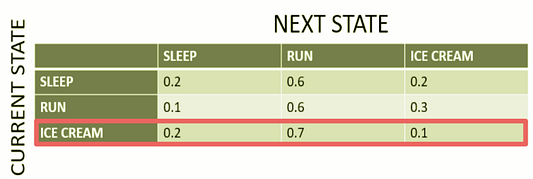
Мы выделили красным цветом строку, на которой сосредоточились, так как текущее состояние (как указано в заголовке строки слева) заключается в том, что Си Джей ест мороженое в течение сегодняшнего дня.

Столбцы представляют следующее состояние, учитывая, что текущее состояние заключается в том, что Си Джей ест мороженое. Вы можете видеть вероятность каждого перехода, например, когда Си Джей ест мороженое сегодня, вероятность того, что на следующий день она будет спать, равна 0,2; отправится на пробежку — 0,7; съест мороженое — 0,1. Три разных столбца выделены разными цветами, чтобы изолировать 3 разностные вероятности перехода состояний.
Ниже приведена конечная переходная матрица.
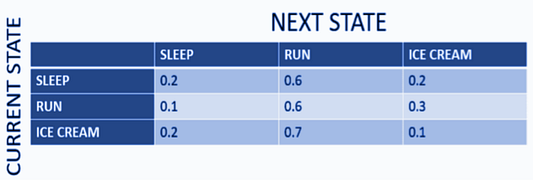
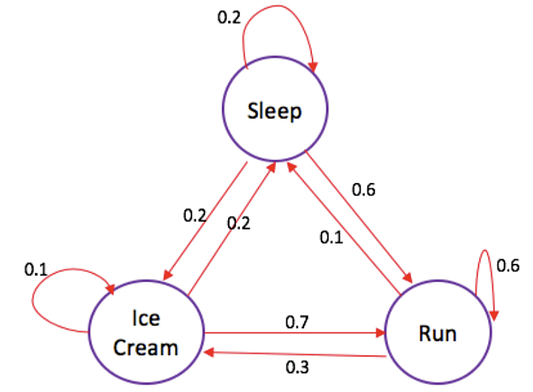
Используя конечную переходную матрицу, мы можем создать цепь Маркова. Для этого отметим все 3 состояния, представляющие ситуацию в настоящее время. Затем создадим переходы между состояниями. Направление стрелки определяет переход от текущего к следующему состоянию. Используя значения из нашей матрицы, подставляем их к соответствующим переходам состояния. Когда текущее состояние равно следующему состоянию, это означает, что Си Джей выполняет одно и то же действие в течение текущего и следующего дня. В этом случае стрелка возвращается к текущему состоянию, поскольку нет перехода в другое состояние.
Дополнительное упражнение
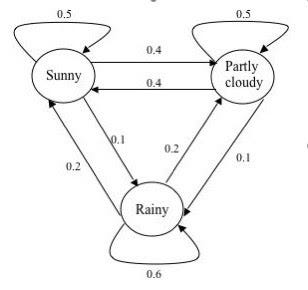
Теперь давайте еще раз взглянем на цепь Маркова, которая моделирует погоду (она была представлена в начале этого поста).
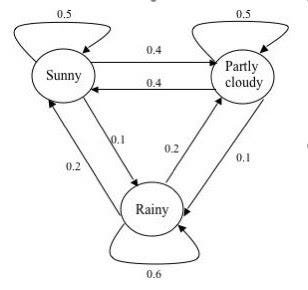
Попытайтесь на основе описанного выше алгоритма создать свою собственную переходную матрицу. Когда закончите, прокрутите страницу вниз, чтобы увидеть конечный результат!
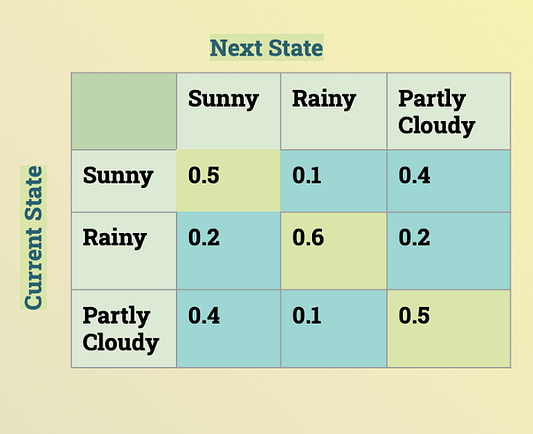
Конечная переходная матрица
Ниже представлена переходная матрица цепи Маркова, которая моделирует погоду. Чтобы ее создать, мы использовали тот же алгоритм, что описан выше, только в обратном направлении.
Заключение
Как вы видели в приведенных выше примерах, цепь Маркова можно использовать в прогнозировании погоды, а также в разработке маркетинговой стратегии, основанной на предположении вероятного поведения потребителя. На основе цепей Маркова созданы такие приложения, как Google PageRank, Subreddit, генератор текстов, автозаполнение слов и предложений. Компании могут использовать эту концепцию для принятия сложных решений, поскольку она позволяет увидеть различные потенциальные решения в доступной визуализированной форме.
Читайте также:
- Машинное обучение без данных
- ИИ-технологии на службе у инфлюенс-маркетинга
- Математические операции над массивами и матрицами
Читайте нас в Telegram, VK и Яндекс.Дзен
Перевод статьи Elda Cervantes, The Markov Chain






