В процессе обработки и организации данных в определенные моменты возникает необходимость в выполнении математических операций над массивами и матрицами.
Заглянем в notebook
Чтобы ознакомиться с рассматриваемыми далее понятиями о математических операциях над массивами и матрицами в NumPy, загляните на страницу с Jupyter Notebook. Обратите внимание: для облегчения понимания важные функции, результаты выполнения и термины выделены жирным шрифтом.
Первым делом разберемся в различиях между массивами и матрицами в NumPy, где эти понятия рассматриваются немного по-разному.
Массив NumPy
Массивы NumPy — это многомерные объекты с размерностью N.
Матрицы NumPy
Матрицы NumPy — это двумерные объекты. По сути, это те же массивы. Но есть массивы с размерностью 3, 4, 5 и т. д., а матрицы представляют собой массивы с размерностью 2.
Математически понятия остались неизменными — в практических и организационных целях разработчики NumPy лишь разделили методы и атрибуты, характерные для объектов-массивов, от тех, что характерны для объектов-матриц. Отметим также, что в операциях линейной алгебры над массивами и матрицами имеются некоторые различия, которые мы позже разберем.
Многие функции в NumPy в качестве получаемого в результате объекта возвращают массивы, а не матрицы. И не забывайте проверять тип объекта. Итак, начнем.
Загрузка пакетов
import sys
import numpy as np
print(sys.version)
np.__version__
3.8.1
'1.19.5'Создание матрицы 1
Создадим массив с помощью матричной функции, в которой передается список значений, заключенных в кавычки“ “, причем эти значения разделенысимволом;. Эта точка с запятой указывает на то, что до ; одна строка, а после ; — другая. Получили массив из 2 строк и 3 столбцов:
mat1 = np.matrix("1,2,3 ; 4,5,6");
mat1[[1 2 3]
[4 5 6]]Проверка типа
Имеем объект-матрицу NumPy (матрицу NumPy), созданную с помощью функции matrix:
type(mat1)
numpy.matrixСоздание матрицы 2
Другой метод создания матриц — список списков. Внутри этого списка еще два списка значений.
mat2 = np.matrix([1,2,3], [4,5,6]]);
mat2[[1 2 3]
[4 5 6]]Создание матрицы 3
С помощью матричной функции создается также матрица со множеством строк и столбцов. При том, что NumPy выделяет создание такой матрицы в отдельную операцию, многомерный объект представляется все так же в виде массива:
mat3 = np.matrix([ [0,10,0,0,0], [0,0,20,0,0], [0,0,0,30,0], [0,0,0,0,40], [0,0,0,0,0]]);
mat3[
[ 0 10 0 0 0]
[ 0 0 20 0 0]
[ 0 0 0 30 0]
[ 0 0 0 0 40]
[ 0 0 0 0 0]]Проверка типа
type(mat3)
numpy.matrix
Получение среза матрицы
Кроме того, получают срез матрицы (не забывая, что индексация в Python начинается с 0):
mat3[2, 3]
30Математические операции
Переходим к выполнению математических операций над массивами и матрицами.
Создание массива
Посмотрите: тип вывода этого объекта — ndarray. То есть его размерность — любое число.
a = np.array([[1,2],[3,4]]);
aarray([[1, 2],
[3, 4]])
type(a)
numpy.ndarrayУмножение массивов
Один массив умножается на другой:
a * aarray([[ 1, 4],
[ 9, 16]])Проверка типа
type(a)
numpy.ndarrayПреобразование массива в матрицу
Для преобразования массива в матрицу используется функция mat, а затем проверяется тип вывода:
A = np.mat(a);
Matrix([[1, 2],
[3, 4]])Обратите внимание: объекты-массивы и объекты-матрицы практически одинаковы. Математически это одно и то же, но у нас для каждого из них есть методы и атрибуты.
Проверка типа
type(A)
numpy.matrixУмножение матриц
Матрицы тоже перемножаются друг с другом:
A * A
matrix([[ 7, 10],
[15, 22]])Почему результаты перемножения массивов и матриц отличаются?
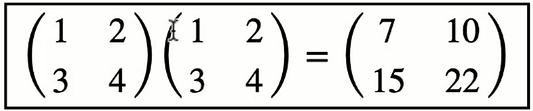
При перемножении массивов происходит непосредственное умножение, т. е. элемент первого массива умножается на соответствующий элемент второго.
Скалярное произведение
При перемножении матриц происходит умножение каждого элемента строки первой матрицы на каждый элемент столбца второй матрицы с суммированием получаемого результата, затем следующий элемент строки первого массива умножается на следующий элемент столбца второго массива и т. д. То есть получаем операцию умножения строки * столбцы:

Этот метод, называющийся скалярным произведением, широко применяется в искусственных нейронных сетях, машинном обучении и искусственном интеллекте, причем практически везде это умножение матриц.
Тем не менее в NumPy выполняется и скалярное произведение массивов. Происходит оно так же, как обычное их умножение:
Скалярное произведение массивов
Мы получили тот же результат, что и при перемножении матриц:
np.dot(a, a)
array([[ 7, 10],
[15, 22]])Преобразование массива в матрицу
Массив в матрицу преобразовывается так:
mat5 = np.asmatrix(a);
mat5matrix([[1, 2],
[3, 4]])
mat5 * mat5
matrix([[ 7, 10],
[15, 22]])Здесь мы воспользовались возможностью преобразования и перемножения матриц — скалярным произведением.
Преобразование матрицы в массив
Преобразуем матрицы в массивы и выполним операции над новым объектом.
array2 = np.asarray(mat5)
array2
array([[1, 2],
[3, 4]])
array2 * array24
array([[ 1, 4],
[ 9, 16]])Обратите внимание: результат операции приводит к умножению массивов на их соответствующие элементы.
Редко где в Интернете найдешь столь простое объяснение. Ведь для понимания этих различий требуются кое-какие математические знания.
Спасибо за внимание.
Читайте также:
- ИИ: постижение законов сверхразума
- 10 идиоматических приемов для эффективного программирования на Python
- Что нужно знать, чтобы начать заниматься квантовыми вычислениями
Читайте нас в Telegram, VK и Яндекс.Дзен
Перевод статьи Anello: Mathematical Operations with Arrays and Matrices






